Giải Toán 8 Bài 4: Bất phương trình bậc nhất một ẩn Giải SGK Toán 8 Tập 2 (trang 47, 48, 49)

Bài trước

Mục lục

Bài sau

Giải bài tập SGK Toán 8 Tập 2 trang 47, 48, 49 giúp các em học sinh lớp 8 xem gợi ý giải các bài tập của Bài 4: Bất phương trình bậc nhất một ẩn. Thông qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 4 Chương 4 trong sách giáo khoa Toán 8 Tập 2.

Giải bài tập Toán 8 tập 2 Bài 4 Chương IV: Bất phương trình bậc nhất một ẩn

Lý thuyết bài 4: Bất phương trình bậc nhất một ẩn

1. Định nghĩa

Bất phương trình dạng ax + b < 0 (hoặc ax + b > 0, ax + b < 0, ax + b ≤ 0, ax + b ≥ 0 ) trong đó a và b là hai số đã cho, a ≠ 0 , được gọi là bất phương trình bậc nhất một ẩn.

2. Hai quy tắc biến đổi bất phương trình

a) Quy tắc chuyển vế

Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.

b) Quy tắc nhân với một số

Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:

- Giữ nguyên chiều bất phương trình nếu số đó dương.

- Đổi chiều bất phương trình nếu số đó âm.

3. Áp dụng

Áp dụng hai quy tắc biến đổi trên, ta giải bất phương trình bậc nhất một ẩn như sau:

Dạng: $ax + b > 0 \Leftrightarrow ax > -b$ $ax + b > 0 \Leftrightarrow ax > -b$

$\Leftrightarrow x > \dfrac{-b}{a}$ $\Leftrightarrow x > \dfrac{-b}{a}$nếu a > 0 hoặc $x < \dfrac{-b}{a}$ $x < \dfrac{-b}{a}$ nếu a < 0.

Vậy nghiệm của bất phương trình ax + b > 0 là:

${S_1} = \left\{ {x|x > \dfrac{ - b}{ a},a > 0} \right\}$ ${S_1} = \left\{ {x|x > \dfrac{ - b}{ a},a > 0} \right\}$ hoặc ${S_2} = \left\{ {x|x < \dfrac{{ - b}}{a},a < 0} \right\}$ ${S_2} = \left\{ {x|x < \dfrac{{ - b}}{a},a < 0} \right\}$

Giải bài tập toán 8 trang 47, 48 tập 2

Bài 19 (trang 47 SGK Toán 8 Tập 2)

Giải các bất phương trình (theo quy tắc chuyển vế):

a) x - 5 > 3

c) -3x > -4x + 2

b) x - 2x < -2x + 4

d) 8x + 2 < 7x - 1

Xem gợi ý đáp án

(Áp dụng quy tắc: chuyển vế - đổi dấu)

a) x - 5 > 3

⇔ x > 3 + 5 (chuyển -5 từ vế trái sang vế phải và đổi dấu thành 5)

⇔ x > 8.

Vậy nghiệm của bất phương trình là x > 8.

b) x - 2x < -2x + 4

⇔ x - 2x + 2x < 4

⇔ x < 4

Vậy nghiệm của bất phương trình là x < 4.

c) -3x > -4x + 2

⇔ -3x + 4x > 2

⇔ x > 2

Vậy nghiệm của bất phương trình là x > 2.

d) 8x + 2 < 7x - 1

⇔ 8x - 7x < -1 - 2

⇔ x < -3

Vậy nghiệm của bất phương trình là x < -3.

Bài 20 (trang 47 SGK Toán 8 Tập 2)

Giải các bất phương trình (theo quy tắc nhân):

a) 0,3x > 0,6

c) -x > 4

b) -4x < 12

d) 1,5x > -9

Xem gợi ý đáp án

a) 0,3x > 0,6

$\Leftrightarrow \dfrac{10}{3}.0,3x > 0,6.\dfrac{10}{3}$ $\Leftrightarrow \dfrac{10}{3}.0,3x > 0,6.\dfrac{10}{3}$ (nhân cả 2 vế với $\dfrac{10}{3}>0$ $\dfrac{10}{3}>0$)

$\Leftrightarrow x > 2$ $\Leftrightarrow x > 2$

Vậy nghiệm của bất phương trình là x> 2.

b) -4x < 12

$\Leftrightarrow \left( { - \dfrac{1}{4}} \right).( - 4x) > 12.\left( { - \dfrac{1}{4}} \right)$ $\Leftrightarrow \left( { - \dfrac{1}{4}} \right).( - 4x) > 12.\left( { - \dfrac{1}{4}} \right)$ (nhân cả 2 vế với $\dfrac{-1}{4}<0$ $\dfrac{-1}{4}<0$)

$\Leftrightarrow x > -3$ $\Leftrightarrow x > -3$

Vậy nghiệm của bất phương trình là x > -3.

c) -x > 4

$\Leftrightarrow \left( { - x} \right).\left( { - 1} \right) < 4.\left( { - 1} \right)$ $\Leftrightarrow \left( { - x} \right).\left( { - 1} \right) < 4.\left( { - 1} \right)$ (nhân cả 2 vế với -1<0)

$\Leftrightarrow x < -4$ $\Leftrightarrow x < -4$

Vậy nghiệm của bất phương trình là x < -4.

d) 1,5x > -9

$\Leftrightarrow \dfrac{3}{2}x > - 9$ $\Leftrightarrow \dfrac{3}{2}x > - 9$

$\Leftrightarrow \dfrac{2}{3}.\dfrac{3}{2}x > - 9.\dfrac{2}{3}$ $\Leftrightarrow \dfrac{2}{3}.\dfrac{3}{2}x > - 9.\dfrac{2}{3}$ (nhân cả 2 vế với $\dfrac{2}{3}>0$ $\dfrac{2}{3}>0$)

$\Leftrightarrow x > -6$ $\Leftrightarrow x > -6$

Vậy nghiệm của bất phương trình là x > -6.

Bài 21 (trang 47 SGK Toán 8 Tập 2)

Giải thích sự tương đương sau:

a) x - 3 > 1 ⇔ x + 3 > 7 b) -x < 2 ⇔ 3x > -6

Xem gợi ý đáp án

a) x – 3 > 1

⇔ x – 3 + 6 > 1 + 6 (Cộng 6 vào cả hai vế).

Hay x + 3 > 7..

Vậy hai bpt trên tương đương.

b) –x < 2

⇔ (-x).(-3) > 2.(-3) (Nhân cả hai vế với -3 < 0, BPT đổi dấu)

⇔ 3x > -6.

Vậy hai BPT trên tương đương.

Bài 22 (trang 47 SGK Toán 8 Tập 2)

Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:

a) 1,2x < -6 ; b) 3x + 4 > 2x + 3

Xem gợi ý đáp án

a) 1,2x < -6

⇔1,2 x : 1,2 < -6 : 1,2

⇔ x < - 5

Vậy nghiệm của bất phương trình là x < -5.

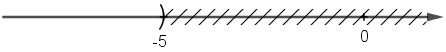
Bài 22

b) 3x + 4 > 2x + 3

⇔ 3x - 2x > 3 - 4 (chuyển vế 2x và 4, đổi dấu hạng tử).

⇔ x > -1

Vậy nghiệm của bất phương trình là x > -1.

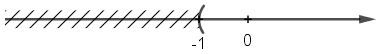
Bài 22

Bài 23 (trang 47 SGK Toán 8 Tập 2)

Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:

a) 2x - 3 > 0 ;

c) 4 - 3x ≤ 0 ;

b) 3x + 4 < 0

d) 5 - 2x ≥ 0

Xem gợi ý đáp án

$\eqalign{& \,\,2x - 3 > 0 \cr & \Leftrightarrow 2x > 3 \cr & \Leftrightarrow x > {3 \over 2} \cr}$ $\eqalign{& \,\,2x - 3 > 0 \cr & \Leftrightarrow 2x > 3 \cr & \Leftrightarrow x > {3 \over 2} \cr}$

Vậy tập nghiệm của bất phương trình là: $S = \left\{ {x\,|\,x > \dfrac{3}{2}} \right\}$ $S = \left\{ {x\,|\,x > \dfrac{3}{2}} \right\}$

Biểu diễn tập nghiệm trên trục số:

Bài 23

$\eqalign{ & \,\,3x + 4 < 0 \cr & \Leftrightarrow 3x < - 4 \cr & \Leftrightarrow x < {{ - 4} \over 3} \cr}$ $\eqalign{ & \,\,3x + 4 < 0 \cr & \Leftrightarrow 3x < - 4 \cr & \Leftrightarrow x < {{ - 4} \over 3} \cr}$

Vậy tập nghiệm của bất phương trình là: $S = \left\{ {x\,|\,x < \dfrac{{ - 4}}{3}} \right\}$ $S = \left\{ {x\,|\,x < \dfrac{{ - 4}}{3}} \right\}$

Biểu diễn tập nghiệm trên trục số:

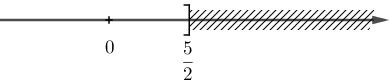
Bài 23

$\eqalign{ & \,\,4 - 3x \le 0 \cr & \Leftrightarrow - 3x \le - 4 \cr & \Leftrightarrow \left( {{{ - 1} \over 3}} \right).\left( { - 3x} \right) \ge \left( { - 4} \right).\left( {{{ - 1} \over 3}} \right) \cr & \Leftrightarrow x \ge {4 \over 3} \cr}$ $\eqalign{ & \,\,4 - 3x \le 0 \cr & \Leftrightarrow - 3x \le - 4 \cr & \Leftrightarrow \left( {{{ - 1} \over 3}} \right).\left( { - 3x} \right) \ge \left( { - 4} \right).\left( {{{ - 1} \over 3}} \right) \cr & \Leftrightarrow x \ge {4 \over 3} \cr}$

Vậy tập nghiệm của bất phương trình là: $S = \left\{ {x\,|\,x \geqslant \dfrac{4}{3}} \right\}$ $S = \left\{ {x\,|\,x \geqslant \dfrac{4}{3}} \right\}$

Biểu diễn tập nghiệm trên trục số:

Bài 23

$\eqalign{ & \,\,5 - 2x \ge 0 \cr & \Leftrightarrow - 2x \ge - 5 \cr & \Leftrightarrow \left( {{{ - 1} \over 2}} \right).\left( { - 2x} \right) \le \left( { - 5} \right).\left( {{{ - 1} \over 2}} \right) \cr & \Leftrightarrow x \le {5 \over 2} \cr}$ $\eqalign{ & \,\,5 - 2x \ge 0 \cr & \Leftrightarrow - 2x \ge - 5 \cr & \Leftrightarrow \left( {{{ - 1} \over 2}} \right).\left( { - 2x} \right) \le \left( { - 5} \right).\left( {{{ - 1} \over 2}} \right) \cr & \Leftrightarrow x \le {5 \over 2} \cr}$

Vậy tập nghiệm của bất phương trình là: $S = \left\{ {x\,|\,x \leqslant \dfrac{5}{2}} \right\}$ $S = \left\{ {x\,|\,x \leqslant \dfrac{5}{2}} \right\}$

Biểu diễn tập nghiệm trên trục số:

Bài 23

Bài 24 (trang 47 SGK Toán 8 Tập 2)

Giải các bất phương trình:

a) 2x - 1 > 5 ;

c) 2 - 5x ≤ 17 ;

b) 3x - 2 < 4

d) 3 - 4x ≥ 19

Xem gợi ý đáp án

a) 2x - 1 > 5

⇔ 2x > 1 + 5 (Chuyển vế và đổi dấu hạng tử -1)

⇔ 2x > 6

⇔ x > 3 (Chia cả hai vế cho 2 > 0, BPT không đổi chiều).

Vậy nghiệm của bất phương trình là x > 3.

b) 3x - 2 < 4

⇔ 3x < 4 + 2 (Chuyển vế và đổi dấu hạng tử -2)

⇔ 3x < 6

⇔ x < 2 (Chia cả hai vế cho 3 > 0, BPT không đổi chiều).

Vậy nghiệm của bất phương trình là x < 2.

c) 2 - 5x ≤ 17

⇔ -5x ≤ 17 - 2 (Chuyển vế và đổi dấu hạng tử 2)

⇔ -5x ≤ 15

⇔ x ≥ -3 (Chia cả hai vế cho -5 < 0, BPT đổi chiều).

Vậy nghiệm của bất phương trình là x ≥ - 3

d) 3 - 4x ≥ 19

⇔ -4x ≥ 19 - 3 (Chuyển vế và đổi dấu hạng tử 3)

⇔ -4x ≥ 16

⇔ x ≤ -4 (Chia cả hai vế cho -4 < 0, BPT đổi chiều).

Vậy nghiệm của bất phương trình là x ≤ -4

Bài 25 (trang 47 SGK Toán 8 Tập 2)

Giải các bất phương trình:

a) $\dfrac{2}{3}x > -6$ $\dfrac{2}{3}x > -6$

c) $3-\dfrac{1}{4}x >2$ $3-\dfrac{1}{4}x >2$

b) $-\dfrac{5}{6}x < 20$ $-\dfrac{5}{6}x < 20$

d) $5 - \dfrac{1}{3}x > 2$ $5 - \dfrac{1}{3}x > 2$

Xem gợi ý đáp án

a) $\dfrac{2}{3}x > -6$ $\dfrac{2}{3}x > -6$

$\eqalign{ & \,\,{2 \over 3}x > - 6 \cr & \Leftrightarrow {3 \over 2}.{2 \over 3}x > {3 \over 2}.\left( { - 6} \right) \cr & \Leftrightarrow x > - 9 \cr}$ $\eqalign{ & \,\,{2 \over 3}x > - 6 \cr & \Leftrightarrow {3 \over 2}.{2 \over 3}x > {3 \over 2}.\left( { - 6} \right) \cr & \Leftrightarrow x > - 9 \cr}$

Vậy nghiệm của bất phương trình là x > -9

b) $-\dfrac{5}{6}x < 20$ $-\dfrac{5}{6}x < 20$

$\eqalign{ & \, - {5 \over 6}x < 20 \cr & \Leftrightarrow \left( { - {6 \over 5}} \right).\left( { - {5 \over 6}} \right).x > 20.\left( { - {6 \over 5}} \right) \cr & \Leftrightarrow x > - 24 \cr}$ $\eqalign{ & \, - {5 \over 6}x < 20 \cr & \Leftrightarrow \left( { - {6 \over 5}} \right).\left( { - {5 \over 6}} \right).x > 20.\left( { - {6 \over 5}} \right) \cr & \Leftrightarrow x > - 24 \cr}$

Vậy nghiệm của bất phương trình là x > -24.

c) $3-\dfrac{1}{4}x >2$ $3-\dfrac{1}{4}x >2$

$\eqalign{ & \,3 - {1 \over 4}x > 2 \cr & \Leftrightarrow - {1 \over 4}x > 2 - 3 \cr & \Leftrightarrow - {1 \over 4}x > - 1 \cr & \Leftrightarrow \left( { - 4} \right).\left( { - {1 \over 4}} \right).x < \left( { - 1} \right).\left( { - 4} \right) \cr & \Leftrightarrow x < 4 \cr}$ $\eqalign{ & \,3 - {1 \over 4}x > 2 \cr & \Leftrightarrow - {1 \over 4}x > 2 - 3 \cr & \Leftrightarrow - {1 \over 4}x > - 1 \cr & \Leftrightarrow \left( { - 4} \right).\left( { - {1 \over 4}} \right).x < \left( { - 1} \right).\left( { - 4} \right) \cr & \Leftrightarrow x < 4 \cr}$

Vậy nghiệm của bất phương trình là x < 4

d) $5 - \dfrac{1}{3}x > 2$ $5 - \dfrac{1}{3}x > 2$

$\eqalign{ & \,\,5 - {1 \over 3}x > 2 \cr & \Leftrightarrow - {1 \over 3}x > 2 - 5 \cr & \Leftrightarrow - {1 \over 3}x > - 3 \cr & \Leftrightarrow \left( { - 3} \right).\left( { - {1 \over 3}} \right).x < \left( { - 3} \right).\left( { - 3} \right) \cr & \Leftrightarrow x < 9 \cr}$ $\eqalign{ & \,\,5 - {1 \over 3}x > 2 \cr & \Leftrightarrow - {1 \over 3}x > 2 - 5 \cr & \Leftrightarrow - {1 \over 3}x > - 3 \cr & \Leftrightarrow \left( { - 3} \right).\left( { - {1 \over 3}} \right).x < \left( { - 3} \right).\left( { - 3} \right) \cr & \Leftrightarrow x < 9 \cr}$

Vậy nghiệm của bất phương trình là x < 9.

Bài 26 (trang 47 SGK Toán 8 Tập 2)

Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào? (Kể ba bất phương trình có cùng tập nghiệm).

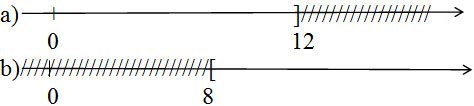
Bài 26

Xem gợi ý đáp án

a) Hình a) biểu diễn tập nghiệm của bất phương trình:

x ≤ 12 hoặc x + 4 ≤ 16 hoặc 2x + 1 ≤ 25

b) Hình biểu diễn tập nghiệm của bất phương trình:

x ≥ 8 hoặc x + 3 ≥ 11 hoặc 3 – 2x ≤ -13.

Bài 27 (trang 48 SGK Toán 8 Tập 2)

Đố: Kiểm tra xem giá trị x = -2 có là nghiệm của bất phương trình sau không?

a) x + 2x² – 3x³ + 4x⁴ – 5 < 2x² – 3x³ + 4x⁴ – 6;

b) (-0,001)x > 0,003.

Xem gợi ý đáp án

a) x + 2x² - 3x³ + 4x⁴ - 5 < 2x² - 3x³ + 4x⁴ - 6

⇔ x < 2x² - 3x³ + 4x⁴ - 6 - 2x² + 3x³ - 4x⁴ + 5 (chuyển vế - đổi dấu)

⇔ x < -1 (*)

Vì -2 < -1 nên -2 là nghiệm của bất phương trình

Vậy x = -2 là nghiệm của bất phương trình.

b) (-0,001)x > 0,003

⇔ x < -3 (chia cả hai vế cho -0,001)

Vì -2 > -3 nên -2 không phải nghiệm của bất phương trình

Vậy x = -2 không là nghiệm của bất phương trình.

Giải bài tập toán 8 trang 48, 49 tập 2: Luyện tập

Bài 28 (trang 48 SGK Toán 8 Tập 2)

Cho bất phương trình x² > 0.

a) Chứng tỏ x = 2, x = -3 là nghiệm của bất phương trình đã cho.

b) Có phải mọi giá trị của ẩn x đều là nghiệm của bất phương trình đã cho hay không?

Xem gợi ý đáp án

a) Thay x = 2 vào bất phương trình ta được: x² = 2² = 4 > 0

Vậy x = 2 là một nghiệm của bất phương trình x² > 0.

Thay x = -3 vào bất phương trình ta được x² = (-3)² = 9 > 0

Vậy x = -3 là một nghiệm của bất phương trình x² > 0.

b) Với x = 0 ta có x² = 0² = 0

⇒ x = 0 không phải nghiệm của bất phương trình x² > 0.

Vậy không phải mọi giá trị của ẩn x đều là nghiệm của bất phương trình đã cho.

Bài 29 (trang 48 SGK Toán 8 Tập 2)

Tìm x sao cho:

a) Giá trị của biểu thức 2x - 5 không âm.

b) Giá trị của biểu thức -3x không lớn hơn giá trị của biểu thức -7x + 5.

Xem gợi ý đáp án

a) Giá trị của biểu thức 2x - 5 không âm tức là:

2x -5 ≥ 0

⇔ 2x ≥5 (Chuyển vế và đổi dấu hạng tử -5)

$\Leftrightarrow x ≥\dfrac{5}{2}$ $\Leftrightarrow x ≥\dfrac{5}{2}$ (Chia cả hai vế cho 2 > 0, BPT không đổi chiều)

Vậy để giá trị của biểu thức 2x - 5 không âm thì $x \geqslant \dfrac{5}{2}$ $x \geqslant \dfrac{5}{2}$

b) Giá trị của biểu thức -3x không lớn hơn giá trị của biểu thức -7x + 5 tức là:

-3x ≤ -7x + 5

⇔ -3x + 7x ≤ 5 (Chuyển vế và đổi dấu hạng tử -7x)

⇔ 4x ≤ 5

$\Leftrightarrow x \leqslant \dfrac{5}{4}$ $\Leftrightarrow x \leqslant \dfrac{5}{4}$

Vậy để cho giá trị của -3x không lớn hơn giá trị của -7x + 5 thì $x \leqslant \dfrac{5}{4}$ $x \leqslant \dfrac{5}{4}$

Bài 30 (trang 48 SGK Toán 8 Tập 2)

Một người có số tiền không quá 70000 đồng gồm 15 tờ giấy bạc với hai loại mệnh giá: loại 2000 đồng và loại 5000 đồng. Hỏi người đó có bao nhiêu tờ giấy bạc loại 5000 đồng?

Xem gợi ý đáp án

Gọi x là số tờ giấy bạc loại 5000 đồng. (với 0 < x < 15, x nguyên)

Số tờ giấy bạc loại 2000 đồng là 15 - x

Vì số tiền không quá 70000 đồng nên ta có bất phương trình sau:

5000x + 2000(15 - x ) ≤ 70000

$\Leftrightarrow 5000x + 30000 - 2000x ≤ 70000$ $\Leftrightarrow 5000x + 30000 - 2000x ≤ 70000$

$\Leftrightarrow 3000x ≤ 40000$ $\Leftrightarrow 3000x ≤ 40000$

$\Leftrightarrow x \leqslant 40000:3000$ $\Leftrightarrow x \leqslant 40000:3000$

$\Leftrightarrow x \leqslant \dfrac{{40}}{3}$ $\Leftrightarrow x \leqslant \dfrac{{40}}{3}$

Kết hợp với điều kiện thì $0 < x \leqslant \dfrac{{40}}{3}$ $0 < x \leqslant \dfrac{{40}}{3}$ mà x là số nguyên nên x có thể là số nguyên dương từ 1 đến 13

Vậy số tờ giấy bạc loại 5000 đồng người ấy có thể có là các số nguyên dương từ 1 đến 13.

Bài 31 (trang 48 SGK Toán 8 Tập 2)

Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:

a) $\dfrac{{15 - 6x}}{3} > 5$ $\dfrac{{15 - 6x}}{3} > 5$

c) $\dfrac{1}{4}\left( {x - 1} \right) < \dfrac{{x - 4}}{6}$ $\dfrac{1}{4}\left( {x - 1} \right) < \dfrac{{x - 4}}{6}$

b) $\dfrac{{8 - 11x}}{4} < 13$ $\dfrac{{8 - 11x}}{4} < 13$

d) $\dfrac{{2 - x}}{3} < \dfrac{{3 - 2x}}{5}$ $\dfrac{{2 - x}}{3} < \dfrac{{3 - 2x}}{5}$

Xem gợi ý đáp án

a) Ta có

$\eqalign{ & {{15 - 6x} \over 3} > 5 \cr & \Leftrightarrow 15 - 6x > 5.3 \cr & \Leftrightarrow 15 - 6x > 15 \cr & \Leftrightarrow - 6x > 0 \cr & \Leftrightarrow x < 0 \cr}$ $\eqalign{ & {{15 - 6x} \over 3} > 5 \cr & \Leftrightarrow 15 - 6x > 5.3 \cr & \Leftrightarrow 15 - 6x > 15 \cr & \Leftrightarrow - 6x > 0 \cr & \Leftrightarrow x < 0 \cr}$

Vậy nghiệm là x < 0 và được biểu diễn trên trục số như sau:

Bài 31

b) Ta có

$\eqalign{ & {{8 - 11x} \over 4} < 13 \cr & \Leftrightarrow 8 - 11x < 13.4 \cr & \Leftrightarrow - 11x < 44 \cr & \Leftrightarrow x > - 4 \cr}$ $\eqalign{ & {{8 - 11x} \over 4} < 13 \cr & \Leftrightarrow 8 - 11x < 13.4 \cr & \Leftrightarrow - 11x < 44 \cr & \Leftrightarrow x > - 4 \cr}$

Vậy nghiệm là x > - 4 và được biểu diễn trên trục số như sau:

Bài 31

c) Ta có

$\eqalign{ & {1 \over 4}\left( {x - 1} \right) < {{x - 4} \over 6} \cr & \Leftrightarrow 12.{1 \over 4}\left( {x - 1} \right) < 12.{{x - 4} \over 6} \cr & \Leftrightarrow 3x - 3 < 2x - 8 \cr & \Leftrightarrow x < - 5 \cr}$ $\eqalign{ & {1 \over 4}\left( {x - 1} \right) < {{x - 4} \over 6} \cr & \Leftrightarrow 12.{1 \over 4}\left( {x - 1} \right) < 12.{{x - 4} \over 6} \cr & \Leftrightarrow 3x - 3 < 2x - 8 \cr & \Leftrightarrow x < - 5 \cr}$

Vậy nghiệm là x < - 5 và được biểu diễn trên trục số như sau:

Bài 31

d) Ta có

$\eqalign{ & {{2 - x} \over 3} < {{3 - 2x} \over 5} \cr & \Leftrightarrow 10 - 5x < 9 - 6x \cr & \Leftrightarrow x < - 1 \cr}$ $\eqalign{ & {{2 - x} \over 3} < {{3 - 2x} \over 5} \cr & \Leftrightarrow 10 - 5x < 9 - 6x \cr & \Leftrightarrow x < - 1 \cr}$

Vậy nghiệm là x < - 1 và được biểu diễn trên trục số như sau:

Bài 31

Bài 32 (trang 48 SGK Toán 8 Tập 2)

Giải các bất phương trình:

a) 8x + 3(x + 1) > 5x - (2x - 6) b) 2x(6x - 1) > (3x - 2)(4x + 3)

Xem gợi ý đáp án

a) 8x + 3(x + 1) > 5x - (2x - 6)

⇔ 8x + 3x + 3 > 5x – 2x + 6

⇔ 8x + 3x - 5x + 2x > 6 - 3

⇔ 8x > 3

$\Leftrightarrow x > \dfrac{3}{8}$ $\Leftrightarrow x > \dfrac{3}{8}$ (Chia cả hai vế cho 8 > 0, BPT không đổi chiều)

Vậy nghiệm của bất phương trình: $x > \dfrac{3}{8}$ $x > \dfrac{3}{8}$

b) 2x(6x - 1) > (3x - 2)(4x + 3)

$\eqalign{ & \Leftrightarrow 12{x^2} - 2x > 12{x^2} + 9x - 8x - 6 \cr & \Leftrightarrow 12{x^2} - 2x > 12{x^2} + x - 6 \cr & \Leftrightarrow 12{x^2} - 2x - 12{x^2} - x > - 6 \cr & \Leftrightarrow - 3x > - 6 \cr & \Leftrightarrow x < \left( { - 6} \right):\left( { - 3} \right) \cr & \Leftrightarrow x < 2 \cr}$ $\eqalign{ & \Leftrightarrow 12{x^2} - 2x > 12{x^2} + 9x - 8x - 6 \cr & \Leftrightarrow 12{x^2} - 2x > 12{x^2} + x - 6 \cr & \Leftrightarrow 12{x^2} - 2x - 12{x^2} - x > - 6 \cr & \Leftrightarrow - 3x > - 6 \cr & \Leftrightarrow x < \left( { - 6} \right):\left( { - 3} \right) \cr & \Leftrightarrow x < 2 \cr}$

Vậy nghiệm của bất phương trình là x < 2.

Bài 33 (trang 48, 49 SGK Toán 8 Tập 2)

Đố: Trong một kì thi, bạn Chiến phải thi bốn môn Văn, Toán, Tiếng Anh và Hóa. Chiến đã thi ba môn và được kết quả như bảng sau:

Môn	Văn	Tiếng Anh	Hóa
Điểm	8	7	10

Kì thi quy định muốn đạt loại giỏi phải có điểm trung bình các môn thi là 8 trở lên và không có môn nào bị điểm dưới 6. Biết môn Văn và Toán được tính hệ số 2. Hãy cho biết, để đạt loại giỏi bạn Chiến phải có điểm thi môn Toán ít nhất là bao nhiêu?

Xem gợi ý đáp án

Gọi x là điểm thi môn Toán, theo đề bài ta có điều kiện: 6 ≤ x ≤ 10.

Vì môn Văn và Toán được tính hệ số 2 nên ta có điểm trung bình bốn môn của Chiến là:

$\dfrac{{8.2 + 7 + 10 + x.2}}{6} = \dfrac{{33 + 2x}}{6}$ $\dfrac{{8.2 + 7 + 10 + x.2}}{6} = \dfrac{{33 + 2x}}{6}$

Để được xếp loại giỏi thì điểm trung bình các môn thi là 8 trở lên nên ta có bất phương trình:

$\dfrac{{33 + 2x}}{6} \geqslant 8$ $\dfrac{{33 + 2x}}{6} \geqslant 8$

$\Leftrightarrow 33 + 2x \geqslant 8.6$ $\Leftrightarrow 33 + 2x \geqslant 8.6$

⇔33 + 2x ≥ 48

$\Leftrightarrow 2x \geqslant 48 - 33$ $\Leftrightarrow 2x \geqslant 48 - 33$

⇔2x ≥ 15

$\Leftrightarrow x \geqslant 15:2$ $\Leftrightarrow x \geqslant 15:2$

⇔x ≥ 7,5

Vậy để đạt được loại giỏi thì bạn Chiến phải có điểm thi môn Toán ít nhất là 7,5.

Bài 34 (trang 49 SGK Toán 8 Tập 2)

Đố: Tìm sai lầm trong các "lời giải" sau:

a) Giải bất phương trình -2x > 23. Ta có:

-2x > 23 ⇔ x > 23 + 2 ⇔ x > 25.

Vậy nghiệm của bất phương trình là x > 25.

b) Giải bất phương trình $- \dfrac{3}{7}x > 12$ $- \dfrac{3}{7}x > 12$ . Ta có:

$- \dfrac{3}{7}x > 12$ $- \dfrac{3}{7}x > 12$

$\Leftrightarrow \left( { - \dfrac{7}{3}} \right).\left( { - \dfrac{3}{7}}x \right) > \left( { - \dfrac{7}{3}} \right).12$ $\Leftrightarrow \left( { - \dfrac{7}{3}} \right).\left( { - \dfrac{3}{7}}x \right) > \left( { - \dfrac{7}{3}} \right).12$

$\Leftrightarrow x > - 28$ $\Leftrightarrow x > - 28$

Vậy nghiệm của bất phương trình là x > -28.

Xem gợi ý đáp án

a) Sai lầm là coi -2 là hạng từ và chuyển vế hạng tử này trong khi -2 là một nhân tử.

Lời giải đúng:

-2x > 23

⇔ x < 23 : (-2) (chia cho số âm nên đổi chiều)

⇔ x < -11,5

Vậy nghiệm của bất phương trình là x < -11,5

b) Sai lầm là khi nhân hai vế của bất phương trình với $\left( { - \dfrac{7}{3}} \right)$ $\left( { - \dfrac{7}{3}} \right)$ mà không đổi chiều bất phương trình.

Lời giải đúng:

$- \dfrac{3}{7}x > 12$ $- \dfrac{3}{7}x > 12$

$\Leftrightarrow \left( { - \dfrac{7}{3}} \right).\left( { - \dfrac{3}{7}x} \right) < \left( { - \dfrac{7}{3}} \right).12$ $\Leftrightarrow \left( { - \dfrac{7}{3}} \right).\left( { - \dfrac{3}{7}x} \right) < \left( { - \dfrac{7}{3}} \right).12$

⇔ x < -28

Vậy nghiệm của bất phương trình là x < -28.

Chia sẻ bởi: