Toán 8 Luyện tập chung trang 108 Giải Toán 8 Kết nối tri thức tập 2 trang 108, 109

Bài trước

Mục lục

Bài sau

Toán 8 Luyện tập chung là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Kết nối tri thức với cuộc sống tập 2 trang 108, 109.

Giải Toán 8 Kết nối tri thức tập 2 trang 108, 109 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập bài Luyện tập chung Chương IX: Tam giác đồng dạng. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:

Toán 8 Luyện tập chung trang 108 Kết nối tri thức

Giải Toán 8 Kết nối tri thức Tập 2 trang 109

Giải Toán 8 Kết nối tri thức Tập 2 trang 109

Bài 9.32

Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng $BH=16cm$, $CH=9cm$

a) Tính độ dài đoạn thẳng AH

b) Tính độ dài đoạn thằng AB và AC

Lời giải:

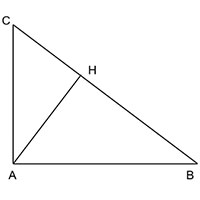
Bài 9.32

a) Có $BC=BH+CH=16+9=25$

Xét tam giác AHC vuông tại H có: $AH^{2}=AC^{2}-CH^{2}$ $AH^{2}=AC^{2}-CH^{2}$ (định lý Pythagore) (1)

Xét tam giác AHB vuông tại H có: $AH^{2}=AB^{2}-BH^{2}$ $AH^{2}=AB^{2}-BH^{2}$ (định lý Pythagore) (2)

Xét (1) + (2), có:

$2AH^{2}=AC^{2}-CH^{2}+AB^{2}-BH^{2}$ $2AH^{2}=AC^{2}-CH^{2}+AB^{2}-BH^{2}$

$2AH^{2}=BC^{2}-CH^{2}-BH^{2}$ $2AH^{2}=BC^{2}-CH^{2}-BH^{2}$

$2AH^{2}=25^{2}-9^{2}-16^{2}$ $2AH^{2}=25^{2}-9^{2}-16^{2}$

$2AH^{2}=288$ $2AH^{2}=288$

$AH^{2}=144$ $AH^{2}=144$

$AH=12 (cm)$

b) Có $AC^{2}=AH^{2}+CH^{2}$ $AC^{2}=AH^{2}+CH^{2}$ (định lý Pythagore)

=> $AC^{2}=12^{2}+9^{2}=225$ $AC^{2}=12^{2}+9^{2}=225$

=> $AC=15(cm)$

Có $AB^{2}=AH^{2}+BH^{2}$ $AB^{2}=AH^{2}+BH^{2}$ (định lý Pythagore)

=> $AB^{2}=12^{2}+16^{2}=400$ $AB^{2}=12^{2}+16^{2}=400$

=> $AB=20(cm)$

Bài 9.33

Cho tam giác ABC có $AB=6cm$, $AC=8cm$, $BC=10cm$. Cho điểm M nằm trên cạnh BC sao cho $BM=4cm$. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB

Lời giải:

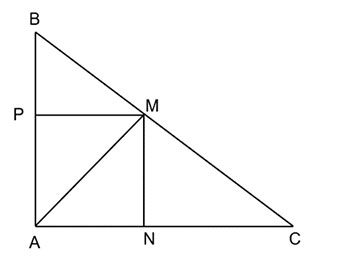
Bài 9.33

a) Ta thấy $AB^{2}+AC^{2}=BC^{2}$ $AB^{2}+AC^{2}=BC^{2}$

=> Tam giác ABC vuông tại A

Có AC ⊥ AB

mà MP ⊥ AB

=> MP // AC

=> $\widehat{BMP}=\widehat{MCN}$ $\widehat{BMP}=\widehat{MCN}$ (2 góc đồng vị)

Xét tam giác vuông BMP (vuông tại P) và tam giác MCN (vuông tại N) có $\widehat{BMP}=\widehat{MCN}$ $\widehat{BMP}=\widehat{MCN}$

=> $\Delta BMP$ $\Delta BMP$ ~ $\Delta MCN$ $\Delta MCN$

b) Xét tam giác BMP và tam giác BAC có MP // AC

=> $\widehat{BPM}=\widehat{BAC}$ $\widehat{BPM}=\widehat{BAC}$

=> $\frac{4}{10}=\frac{PM}{8}$ $\frac{4}{10}=\frac{PM}{8}$

=> $PM=3,2(cm)$

=> $BP=2,4$ (áp dụng định lý Pythagore trong tam giác vuông BMP)

=> $AP=3,6$ (cm)

=> $AM=\sqrt{23.2}$ $AM=\sqrt{23.2}$ (áp dụng định lý Pythagore trong tam giác vuông AMP)

Bài 9.34

Trong hình 9.72, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng

a) $\Delta AEH$ $\Delta AEH$ ~ $\Delta AHB$ $\Delta AHB$

b) $\Delta AFH$ $\Delta AFH$ ~ $\Delta AHC$ $\Delta AHC$

c) $\Delta AFE$ $\Delta AFE$ ~ $\Delta ABC$ $\Delta ABC$

Bài 9.34

Bài 9.35

Cho tam giác ABC vuông tại A có đường cao AH. Cho M và N lần lượt là trung điểm của AB và AC. Chứng minh $\Delta HBM$ $\Delta HBM$ ~ $\Delta HAN$ $\Delta HAN$

Bài 9.36

Vào gần buổi trưa, khi bóng bạn An dài 60 cm thì bóng cột cờ dài 3m

a) Biết rằng bạn An cao 1,4 m. Hỏi cột cờ cao bao nhiêu mét?

b) Vào buổi chiều khi bóng bạn An dài 3m, hỏi bóng cột cờ dài bao nhiêu mét?

Chia sẻ bởi:

Lê Thị tuyết Mai

Tải về

Liên kết tải về

Toán 8 Luyện tập chung trang 108 170,6 KB Tải về

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!