Toán 8 Bài 35: Định lí Pythagore và ứng dụng Giải Toán 8 Kết nối tri thức tập 2 trang 93, 94, 95, 96, 97
Giải bài tập Toán 8 Bài 35: Định lí Pythagore và ứng dụng với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa SGK Toán 8 Kết nối tri thức với cuộc sống tập 2 trang 93, 94, 95, 96, 97. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.
Giải Toán 8 Bài 35 chi tiết, còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của Bài 35 Chương IX: Tam giác đồng dạng. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:
Toán 8 Bài 35: Định lí Pythagore và ứng dụng Kết nối tri thức
Phần Luyện tập
Luyện tập 1 Toán 8 trang 95 Tập 2
Trên giấy kẻ ô vuông (cạnh ô vuông bằng 1 cm), cho các điểm A, B, C như Hình 9.35. Tính độ dài các cạnh của tam giác ABC.
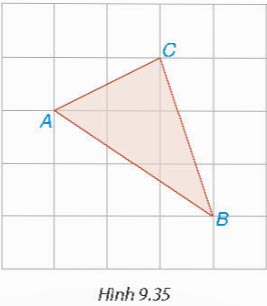
Lời giải:
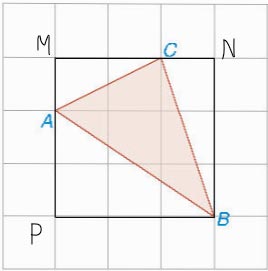
Gọi các điểm M, N, P như hình vẽ.
Áp dụng định lí Pythagore trong tam giác vuông, ta có:
AC2 = 12 + 22 = 5. Suy ra ![]() \(AC=\sqrt{5}\)
\(AC=\sqrt{5}\)
AB2 = 22 + 32 = 13. Suy ra ![]() \(AB=\sqrt{13}\)
\(AB=\sqrt{13}\)
BC2 = 12 + 32 = 10. Suy ra ![]() \(BC=\sqrt{10}\)
\(BC=\sqrt{10}\)
Luyện tập 2 Toán 8 trang 95 Tập 2
Cho tam giác vuông với kích thước như Hình 9.37. Hãy tính độ dài x và cho biết những tam giác nào đồng dạng, viết đúng kí hiệu đồng dạng.
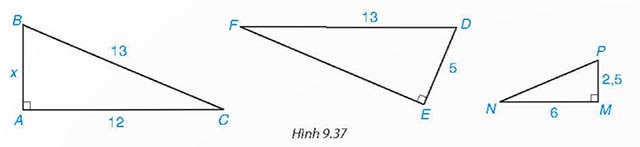
Lời giải:
Áp dụng định lí Pythagore trong tam giác vuông ABC, ta có: x2 + 122 = 132.
Suy ra x = 5.
Vậy ∆ ABC = ∆ EDF (cạnh huyền - cạnh góc vuông) (1)
Xét tam giác ABC và tam giác MPN có:
![]() \(\frac{AB}{MP}=\frac{AC}{MN}=2\)
\(\frac{AB}{MP}=\frac{AC}{MN}=2\)
![]() \(\widehat{BAC}= \widehat{PMN}\)
\(\widehat{BAC}= \widehat{PMN}\)
Do đó ∆ ABC ∽ ∆ MPN (c.g.c) với hệ số đồng dạng k = 2. (2)
Từ (1) và (2) suy ra ∆ EDF ∽ ∆ MPN.
Luyện tập 3 Toán 8 trang 96 Tập 2
Trước đây chúng ta thừa nhận định lí về trường hợp bằng nhau đặc biệt của hai tam giác vuông: "Nếu một cạnh góc vuông và cạnh huyền của tam giác vuông này bằng một cạnh góc vuông và cạnh huyền của tam giác vuông kia thì hai tam giác vuông đó bằng nhau”. Áp dụng định lí Pythagore, em hãy chứng minh định lí trên.
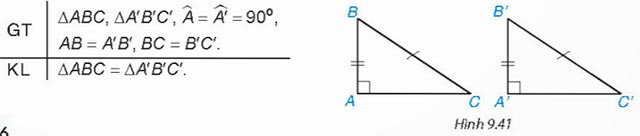
Lời giải:
Áp dụng định Pythagore trong tam giác vuông ABC, ta có:
BC2 = AB2 + AC2.
Suy ra AC2 = BC2 - AB2 = B'C' 2 - A'B' 2 = A'C' 2.
Do đó AC = A'C'
Vậy ∆ABC = ∆A'B'C' (c.c.c).
Phần Bài tập
Bài 9.17 Toán 8 trang 97 Tập 2
Cho tam giác ABC vuông tại A. Trong các khẳng định sau đây, khẳng định nào đúng, khẳng định nào sai
a) ![]() \(AB^{2}+BC^{2}=AC^{2}\)
\(AB^{2}+BC^{2}=AC^{2}\)
b) ![]() \(BC^{2}-AC^{2}=AB^{2}\)
\(BC^{2}-AC^{2}=AB^{2}\)
c) ![]() \(AC^{2}+BC^{2}=AB^{2}\)
\(AC^{2}+BC^{2}=AB^{2}\)
d) ![]() \(BC^{2}-AB^{2}=AC^{2}\)
\(BC^{2}-AB^{2}=AC^{2}\)
Đáp án:
Khẳng định b, d đúng
Khẳng định a, c sai
Bài 9.18 Toán 8 trang 97 Tập 2
Những bộ ba số đo nào dưới đây là độ dài ba cạnh của một tam giác vuông
a) ![]() \(1 cm, 1cm, 2cm\)
\(1 cm, 1cm, 2cm\)
b) ![]() \(2 cm, 4 cm, 20 cm\)
\(2 cm, 4 cm, 20 cm\)
c) ![]() \(5 cm, 4 cm, 3 cm\)
\(5 cm, 4 cm, 3 cm\)
d) ![]() \(2 cm, 2 cm, 2\sqrt{2} cm\)
\(2 cm, 2 cm, 2\sqrt{2} cm\)
Đáp án: c và d
Bài 9.19 Toán 8 trang 97 Tập 2
Tính độ dài x, y, z, t trong Hình 9.43
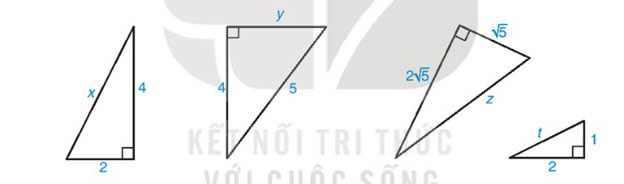
Lời giải:
- ![]() \(x^{2}=4^{2}+2^{2}=20\) =>
\(x^{2}=4^{2}+2^{2}=20\) => ![]() \(x=2\sqrt{5}\)
\(x=2\sqrt{5}\)
- ![]() \(y^{2}=5^{2}-4^{2}=9\) =>
\(y^{2}=5^{2}-4^{2}=9\) => ![]() \(y=3\)
\(y=3\)
- ![]() \(z^{2}=(\sqrt{5})^{2}+(2\sqrt{5})^{2}=25\) =>
\(z^{2}=(\sqrt{5})^{2}+(2\sqrt{5})^{2}=25\) => ![]() \(z=5\)
\(z=5\)
- ![]() \(t^{2}=1^{2}+2^{2}=5\) =>
\(t^{2}=1^{2}+2^{2}=5\) => ![]() \(t=\sqrt{5}\)
\(t=\sqrt{5}\)
Bài 9.20 Toán 8 trang 97 Tập 2
Cho tam giác ABC cân tại đỉnh A, chiều cao ![]() \(AH=3cm\) và cạnh đáy
\(AH=3cm\) và cạnh đáy ![]() \(BC=10cm\). Hãy tính độ dài các cạnh bên AB, AC
\(BC=10cm\). Hãy tính độ dài các cạnh bên AB, AC
Lời giải:
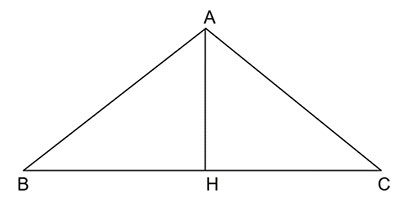
Vì tam giác ABC cân tại A => ![]() \(AB=AC\),
\(AB=AC\), ![]() \(HB=HC=5cm\)
\(HB=HC=5cm\)
Xét tam giác AHB vuông tại H có
![]() \(AB^{2}=AH^{2}+HB^{2}=3^{2}+5^{2}=34\)
\(AB^{2}=AH^{2}+HB^{2}=3^{2}+5^{2}=34\)
=> ![]() \(AB=\sqrt{34}cm\)
\(AB=\sqrt{34}cm\)
Bài 9.21 Toán 8 trang 97 Tập 2
Hãy tính diện tích của một hình chữ nhật có chiều rộng 8cm và đường chéo dài 17cm
Lời giải:
Theo đề bài, ta có hình vẽ:
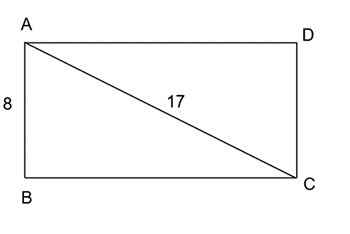
Xét tam giác ABC vuông tại B, có
![]() \(BC^{2}=AC^{2}-AB^{2}=17^{2}-8^{2}=225\)
\(BC^{2}=AC^{2}-AB^{2}=17^{2}-8^{2}=225\)
=> ![]() \(BC=15(cm)\)
\(BC=15(cm)\)
=> Diện tích của hình chữ nhật là: ![]() \(AB.BC=8.15=120(cm^{2})\)
\(AB.BC=8.15=120(cm^{2})\)
Bài 9.22 Toán 8 trang 97 Tập 2
Chú cún bị xích bởi một sợi dây dài 6m để canh một mảnh vườn giới hạn bởi các điểm A, B, E, F, D trong hình vuông ABCD có cạnh 5m như Hình 9.44. Đầu xích buộc cố định tại điểm A của mảnh vườn. Hỏi chú cún có thể chạy đến tất cả các điểm của mảnh vườn mình phải canh không
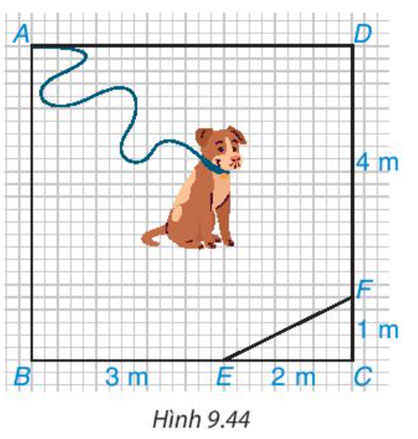
Lời giải:
- Xét tam giác ABE vuông tại B, có
![]() \(AE^{2}=AB^{2}+BE^{2}=5^{2}+3^{2}=34\)
\(AE^{2}=AB^{2}+BE^{2}=5^{2}+3^{2}=34\)
=> ![]() \(AE=\sqrt{34}(m)\)
\(AE=\sqrt{34}(m)\)
=> Chú chó có thể chạy đến điểm E do khoảng cách AE ngắn hơn sợi dây
- Xét tam giác ADF vuông tại D, có
![]() \(AF^{2}=AD^{2}+DF^{2}=5^{2}+4^{2}=41\)
\(AF^{2}=AD^{2}+DF^{2}=5^{2}+4^{2}=41\)
=> ![]() \(AE=\sqrt{41}(m)\)
\(AE=\sqrt{41}(m)\)
=> Chú chó không thể chạy đến điểm F do khoảng cách AF dài hơn sợi dây
- Xét tam giác ADC vuông tại D, có
![]() \(AC^{2}=AD^{2}+DC^{2}=5^{2}+5^{2}=50\)
\(AC^{2}=AD^{2}+DC^{2}=5^{2}+5^{2}=50\)
=> ![]() \(AE=5\sqrt{2}(m)\)
\(AE=5\sqrt{2}(m)\)
=> Chú chó không thể chạy đến điểm C do khoảng cách AC dài hơn sợi dây
Vậy chú chó không thể chạy hết tất cả các điểm của mảnh vườn. Chú chó chỉ có thể chạy đến điểm B, D, E.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:













 Toán 8 Kết nối tri thức
Toán 8 Kết nối tri thức
 Toán 8 Cánh Diều
Toán 8 Cánh Diều
 Toán 8 Chân trời sáng tạo
Toán 8 Chân trời sáng tạo
 Toán 8
Toán 8
 Soạn Văn 8 Kết nối tri thức
Soạn Văn 8 Kết nối tri thức
 Soạn văn 8 Chân trời sáng tạo
Soạn văn 8 Chân trời sáng tạo
 Soạn Văn 8 Cánh Diều
Soạn Văn 8 Cánh Diều
 Chuyên đề Ngữ văn 8
Chuyên đề Ngữ văn 8
 Văn mẫu 8 Kết nối tri thức
Văn mẫu 8 Kết nối tri thức
 Văn mẫu 8 Chân trời sáng tạo
Văn mẫu 8 Chân trời sáng tạo









