Toán 8 Luyện tập chung trang 73 Giải Toán 8 Kết nối tri thức trang 73

Giải Toán lớp 8 Luyện tập chung bao gồm đáp án chi tiết, cùng hướng dẫn giải cho từng bài tập trong SGK Toán 8 Tập 1 Kết nối tri thức với cuộc sống trang 73.

Lời giải Toán 8 Kết nối tri thức trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 8, từ đó học tốt môn Toán lớp 8 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài Luyện tập chung trang 73 Chương III: Tứ giác. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 8 Kết nối tri thức Tập 1 trang 73

Bài 3.34

Cho tam giác ABC; M và N lần lượt là trung điểm của hai cạnh AB và AC. Lấy điểm P sao cho N là trung điểm của đoạn MP

a) Hỏi tứ giác AMCP là hình gì? Vì sao?

b) Với điều kiện nào của tam giác ABC thì tứ giác AMCP là hình chữ nhật; hình thoi; hình vuông?

Hướng dẫn:

Vận dụng các định lí về tính chất và dấu hiệu nhận biết của hình chữ nhật, hình thoi, hình vuông.

Bài giải:

a) Xét tứ giác AMCP có hai đường chéo AC và MP cắt nhau tại trung điểm mỗi đường

Suy ra AMCP là hình bình hành (theo dấu hiệu nhận biết).

b) Để AMCP là hình chữ nhật thì \(\widehat{AMC}=90^{\circ}\)

Khi đó đường trung tuyến CM là trung trực của tam giác ABC, tức là tam giác ABC cân tại C.

+) Để AMCP là hình thoi khi và chỉ khi AMCP có hai cạnh kề bằng nhau

Tức là MA = MB = MC

Do đó tam giác ABC vuông tại C

+) Để AMCP là hình vuông thì AMCP là hình thoi có \(\widehat{AMC}=90^{\circ}\)

Suy ra tam giác ABC vuông cân tại C.

Bài 3.35

Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên Hình 3.58. Chứng minh rằng EFGH là hình chữ nhật.

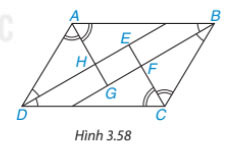
Bài giải:

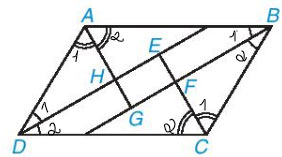
Vì ABCD là hình bình hành nên AB // DC và AD // BC

Do đó \(\widehat{ADC}+\widehat{ADC}=180^{\circ}\)

\(2\widehat{D_2}+2\widehat{C_2}=180^{\circ}\)

\(\widehat{D_2}+\widehat{C_2}=90^{\circ}\) (1)

Xét tam giác EDC có:

\(\widehat{DEC}+\widehat{D_2}+\widehat{C_2}=180^{\circ}\) (định lí tổng ba góc trong tam giác) (2)

Từ (1) và (2) suy ra \(\widehat{DEC} =90^{\circ}\) hay tam giác EDC vuông tại E

Chứng minh tương tự, ta được tam giác AHD vuông tại H, tam giác GAB vuông tại G

Xét tứ giác HEFG có \(\widehat{HEF}=\widehat{EHG}=\widehat{HGF} =90^{\circ}\)

Suy ra HEFG là hình chữ nhật (dấu hiệu nhận biết).

Bài 3.36

Một khung tre hình chữ nhật có lắp đinh vít tại bốn đỉnh. Khi khung tre này bị xô lệch (do các đinh vít bị lỏng), các góc không còn vuông nữa thì khung đó là hình gì? Tại sao? Hỏi khi nẹp thêm một đường chéo vào khung đó thì nó còn bị xô lệch không?

Bài giải:

Khi khung tre này bị xô lệch (do các đinh vít bị lỏng), các góc không còn vuông nữa thì khung đó là hình bình hành (do hình bình có 1 góc vuông thì là hình chữ nhật)

Khi nẹp thêm một đường chéo vào khung đó thì nó không còn bị xô lệch do khung đã được cố định bởi đường chéo nẹp thêm.

Bài 3.37

Gọi Ou và Ov lần lượt là hai tia phân giác của hai góc kề bù xOy và x'Oy; A là một điểm khác O trên tia Ox. Gọi B và C là chân đường vuông góc hạ từ A lần lượt xuống đường thẳng chứa Ou và Ov. Hỏi tứ giác OBAC là hình gì? Vì sao?

Bài giải:

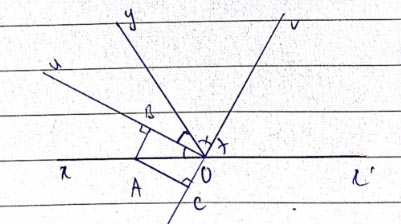
Ta có \(\widehat{uOv}\) là góc tạo bởi hai đường phân giác của hai góc kề bù \(\Rightarrow \widehat{uOv}=90^{\circ}\)

Xét tứ giác OBAC ta có:\(\widehat{OCA}=\widehat{BOC}=\widehat{OBA}=90^{\circ}\) nên OBAC là hình chữ nhật

Bài 3.38

Cho hình vuông ABCD. Lấy một điểm E trên cạnh CD. Tia phân giác của góc DAE cắt cạnh DC tại M. Đường thẳng qua M vuông góc với AE cắt BC tại N. Chứng minh DM + BN = MN

Bài giải:

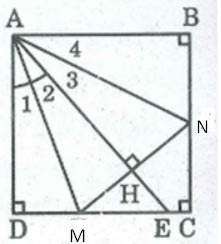
Gọi giao điểm của AE và MN là H

Xét tam giác vuông AMD và AMH ta có:

AM chung

\(\widehat{A1}=\widehat{A2}\)

Suy ra \(\Delta AMD=\Delta AMH (ch - gn) \Rightarrow DM=MH, AD=AH\)

Xét tam giác vuông ANH và ANB ta có:

AN chung

AH = AB (do cùng = AD)

Suy ra \(\Delta ANH=ANB (ch - cgv) \Rightarrow NH =  BN\)

Ta có \(DM = MH, NH = BN \Rightarrow DM+BN=MH+NH=MN\)