Toán 8 Bài 33: Hai tam giác đồng dạng Giải Toán 8 Kết nối tri thức tập 2 trang 78, 79, 80, 81, 82

Giải Toán lớp 8 bài 33: Hai tam giác đồng dạng bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 8 Tập 1 Kết nối tri thức với cuộc sống trang 78, 79, 80, 81, 82.

Lời giải Toán 8 Bài 33 Kết nối tri thức trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 8, từ đó học tốt môn Toán lớp 8 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 33 Chương IX: Tam giác đồng dạng. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 8 Kết nối tri thức Tập 2 Bài 33 - Luyện tập

Luyện tập 1

Trong các tam giác được vẽ trên ô lưới vuông (H.9.3), có một cặp tam giác đồng dạng. Hãy chỉ ra cặp tam giác đó, viết đúng kí hiệu đồng dạng và tìm tỉ số đồng dạng của chúng.

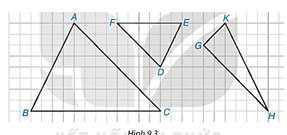
Lời giải:

Ta có ∆ABC ∽ ∆DEF với tỉ số đồng dạng \(\frac{BC}{EF}=\frac{12}{6}=2\)

Nhìn hình vẽ ta thấy tam giác GHK vuông tại G nên không thể đồng dạng với hai tam giác còn lại.

Luyện tập 2

Trong Hình 9.8, các đường thẳng AB, CD, EF song song với nhau. Hãy liệt kê ba cặp tam giác (phân biệt) đồng dạng.

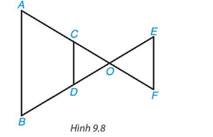
Lời giải:

- Vì C ∊ OA, D ∊ OB và CD //AB nên ∆OCD ∽ ∆OAB.

- Vì E ∊ OB, F ∊ OA (thuộc phần kéo dài) và EF // AB nên ∆OEF ∽ ∆OBA.

- Vì F ∊ OC, E ∊ OD (thuộc phần kéo dài) và EF // CD nên ∆OEF ∽ ∆ODC.

Giải Toán 8 Kết nối tri thức Tập 2 trang 82

Bài 9.1

Cho ΔABC ~ ΔMNP, khẳng định nào sau đây không đúng?

a) ΔMNP ~ ΔABC

b) ΔBCA ~ ΔNPM

c) ΔCAB ~ ΔPNM

d) ΔACB ~ ΔMNP

Lời giải:

Khẳng định d) là khẳng định không đúng

=> ΔACB ~ ΔMPN

Bài 9.2

Khẳng định nào sau đây là đúng?

a) Hai tam giác bằng nhau thì đồng dạng với nhau.

b) Hai tam giác bất kì đồng dạng với nhau

c) Hai tam giác đều bất kì đồng dạng với nhau

d) Hai tam giác vuông bất kì đồng dạng với nhau

e) Hai tam giác đồng dạng thì bằng nhau

Lời giải:

Bài 9.3

Trong hình 9.9, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng

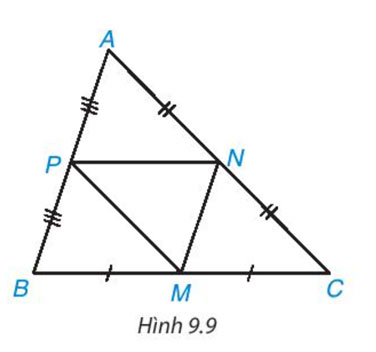
Lời giải:

- Có \(AP=BP\), \(NA=NC\)

=> NP // BC (\(P\in AB, N\in AC\))

=> ΔABC ~ ΔAPN

- Có \(AP=BP\), \(MB=MC\)

=> MP // AC (\(P\in AB, M\in BC\))

=> ΔABC ~ ΔPBM

- Có \(NA=NC\), \(MB=MC\)

=> MN // AB (\(N\in AC, M\in BC\))

=> ΔABC ~ ΔNMC

- Có ΔABC ~ ΔAPN và ΔABC ~ ΔPBM => ΔAPN ~ ΔPBM

- Có ΔABC ~ ΔNMC và ΔABC ~ ΔPBM => ΔNMC ~ ΔPBM

Bài 9.4

Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng \(\widehat{BAC}=\widehat{PMN}, AB=2MN\). Chứng minh ΔMNP ~ ΔABC và tìm tỉ số đồng dạng

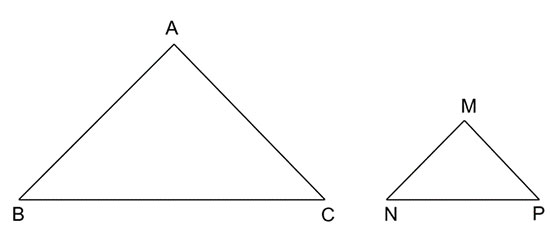
Lời giải:

- Có tam giác ABC cân tại A => \(AB=AC\), \(\widehat{B}=\widehat{C}\)

- Có tam giác MNP cân tại M => \(MN=MP\), \(\widehat{N}=\widehat{P}\)

Mà \(AB=2MN\), \(\widehat{A}=\widehat{M}\)

=> \(\widehat{B}=\widehat{N}=\widehat{C} =\widehat{P}\)

=> \(\frac{MN}{AB}=\frac{MP}{AC}=\frac{NP}{BC}=\frac{1}{2}\)

=> ΔMNP ~ ΔABC với tỉ số đồng dạng là \(\frac{1}{2}\)