Toán 8 Luyện tập chung trang 17 Giải Toán 8 Kết nối tri thức trang 17, 18

Bài trước

Mục lục

Bài sau

Giải bài tập Toán lớp 8 Luyện tập chung với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 8 Tập 1 Kết nối tri thức với cuộc sống trang 17, 18. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 8 chi tiết, còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của bài Luyện tập chung Chương I: Đa thức. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Toán 8 Luyện tập chung Kết nối tri thức

Giải Toán 8 Kết nối tri thức Tập 1 trang 17, 18

Giải Toán 8 Kết nối tri thức Tập 1 trang 17, 18

Bài 1.18

Cho các biểu thức:

$\frac{4}{5}x;(\sqrt{2}-1)xy;-3xy^{2};\frac{1}{2}x^{2}y;\frac{1}{x}y^{3};-xy+\sqrt{2};-\frac{3}{2}x^{2}y;\frac{\sqrt{x}}{5}$ $\frac{4}{5}x;(\sqrt{2}-1)xy;-3xy^{2};\frac{1}{2}x^{2}y;\frac{1}{x}y^{3};-xy+\sqrt{2};-\frac{3}{2}x^{2}y;\frac{\sqrt{x}}{5}$

a) Trong các biểu thức đã cho, biểu thức nào là đơn thức? Biểu thức nào không là đơn thức?

b) Hãy chỉ ra hệ số và phần biến của mỗi đơn thức đã cho.

c) Viết tổng tất cả các đơn thức trên để được một đa thức. Xác định bậc của đa thức đó.

Hướng dẫn giải:

a) Dựa vào định nghĩa Đơn thức: Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của một số và một biến.

b) Trong đơn thức thu gọn, ta xác định:

- Hệ số: phần số.

- Phần biến: phần còn lại (tích các biến trong đơn thức).

- Bậc: Tổng số mũ của các biến trong đơn thức.

c) Đa thức là tổng của các đơn thức

- Bậc của đa thức là bậc của đơn thức thu gọn có bậc cao nhất.

Bài giải:

a) Đơn thức: $\frac{4}{5}x;(\sqrt{2}-1)xy;-3xy^{2};\frac{1}{2}x^{2}y;-\frac{3}{2}x^{2}y$ $\frac{4}{5}x;(\sqrt{2}-1)xy;-3xy^{2};\frac{1}{2}x^{2}y;-\frac{3}{2}x^{2}y$

Không phải đơn thức: $-xy+\sqrt{2};\frac{1}{x}y^{3};\frac{\sqrt{x}}{5}$ $-xy+\sqrt{2};\frac{1}{x}y^{3};\frac{\sqrt{x}}{5}$

b) $\frac{4}{5}x$ $\frac{4}{5}x$ có hệ số là $\frac{4}{5}$ $\frac{4}{5}$, biến là x;

$(\sqrt{2}-1)xy$ $(\sqrt{2}-1)xy$ có hệ số là $\sqrt{2}-1$ $\sqrt{2}-1$, biến là xy

$-3xy^{2}$ $-3xy^{2}$ có hệ số là -3, biến là $xy^{2}$ $xy^{2}$

$\frac{1}{2}x^{2}y$ $\frac{1}{2}x^{2}y$ có hệ số là $\frac{1}{2}$ $\frac{1}{2}$, biến là $x^{2}y$ $x^{2}y$

$-\frac{3}{2}x^{2}y$ $-\frac{3}{2}x^{2}y$ có hệ số là $-\frac{3}{2}$ $-\frac{3}{2}$, biến là $x^{2}y$ $x^{2}y$

c) $\frac{4}{5}x+(\sqrt{2}-1)xy-3xy^{2}+\frac{1}{2}x^{2}y-\frac{3}{2}x^{2}y$ $\frac{4}{5}x+(\sqrt{2}-1)xy-3xy^{2}+\frac{1}{2}x^{2}y-\frac{3}{2}x^{2}y$

$=\frac{4}{5}x+(\sqrt{2}-1)xy-3xy^{2}-x^{2}y$ $=\frac{4}{5}x+(\sqrt{2}-1)xy-3xy^{2}-x^{2}y$

có bậc là 3

Bài 1.19

Trong một khách sạn có hai bể bơi dạng hình hộp chữ nhật. Bể thứ nhất có chiều sâu là 1,2 m, đáy hình hộp chữ nhật có chiều dài x mét, chiều rộng y mét. Bể thứ hai có chiều sâu là 1,5 m, hai kích thước đáy gấp 5 lần hai kích thước đáy của bể thứ nhất.

a) Hãy tìm đơn thức (hai biến x và y) biểu thị số mét khối nước cần có để bơm đầy cả hai bể bơi.

b) Tính lượng nước bơm đầy hai bể nếu x = 4m, y = 3m

Hướng dẫn giải:

a) Số mét khối nước cần có để bơm đầy bể là thể tích của bể bơi dạng hình hộp chữ nhật.

Công thức tính thể tích hình hộp chữ nhật: V = Chiều dài x chiều rộng x chiều cao

b) Viết biểu thức biểu thị lượng nước bơm đầy hai bể, sau đó thay giá trị của x và y vào biểu thức

Bài giải:

a) Số mét khối nước cần có để bơm đầy bể bơi thứ nhất: 1,2xy (m³)

Số mét khối nước cần có để bơm đầy bể bơi thứ hai: $1,5 \times 5x\times 5y=37,5xy (m^{3})$ $1,5 \times 5x\times 5y=37,5xy (m^{3})$

Số mét khối nước cần có để bơm đầy cả hai bể bơi: 1,2xy + 37,5xy = 38,7xy (m³)

b) Lượng nước bơm đầy hai bể nếu x = 4m, y = 3m là: $38,7 \times 4 \times 3=464,4$ $38,7 \times 4 \times 3=464,4$ (m³)

Bài 1.20

Tìm bậc của mỗi đa thức sau rồi tính giá trị của chúng tại x = 1; y = -2

$P=5x^{4}-3x^{3}y+2xy^{3}-x^{3}y+2y^{4}-7x^{2}y^{2}-2xy^{3}$ $P=5x^{4}-3x^{3}y+2xy^{3}-x^{3}y+2y^{4}-7x^{2}y^{2}-2xy^{3}$

$Q=x^{3}+x^{2}y+xy^{2}-x^{2}y-xy^{2}-x^{3}$ $Q=x^{3}+x^{2}y+xy^{2}-x^{2}y-xy^{2}-x^{3}$

Hướng dẫn giải:

- Bước 1: Thu gọn các đa thức

- Bước 2: Xác định bậc của đa thức

- Bước 3: Tính giá trị của các đa thức tại x = 1 và y= - 2

Bài giải:

Ta có $P = 5x^{4} – 3x^{3}y + 2xy^{3} – x^{3}y + 2y^{4} – 7x^{2}y^{2} – 2xy^{3}$ $P = 5x^{4} – 3x^{3}y + 2xy^{3} – x^{3}y + 2y^{4} – 7x^{2}y^{2} – 2xy^{3}$

$= 5x^{4} – (3x^{3}y + x^{3}y) + (2xy^{3} – 2xy^{3}) + 2y^{4} – 7x^{2}y^{2}$ $= 5x^{4} – (3x^{3}y + x^{3}y) + (2xy^{3} – 2xy^{3}) + 2y^{4} – 7x^{2}y^{2}$

$= 5x^{4} – 4x^{3}y + 2y^{4} – 7x^{2}y^{2}$ $= 5x^{4} – 4x^{3}y + 2y^{4} – 7x^{2}y^{2}$

Đa thức P có bậc là 4.

Thay x = 1; y = −2 vào biểu thức P, ta được:

$P = 5 \times 1^{4} – 4 \times 1^{3} \times (−2) + 2\times (−2)^{4} – 7 \times 1^{2} \times (−2)^{2}$ $P = 5 \times 1^{4} – 4 \times 1^{3} \times (−2) + 2\times (−2)^{4} – 7 \times 1^{2} \times (−2)^{2}$

$= 5 – 4 \times (−2) + 2 \times 16 – 7 \times 4$ $= 5 – 4 \times (−2) + 2 \times 16 – 7 \times 4$

= 5 + 8 + 32 – 28 = 13 + 4 = 17.

$Q=x^{3}+x^{2}y+xy^{2}-x^{2}y-xy^{2}-x^{3}=0$ $Q=x^{3}+x^{2}y+xy^{2}-x^{2}y-xy^{2}-x^{3}=0$ Không có bậc xác định

Bài 1.21

Cho hai đa thức:

$A=7xyz^{2}-5xy^{2}z+3x^{2}yz-xyz+1;B=7x^{2}yz-5xy^{2}z+3xyz^{2}-2$ $A=7xyz^{2}-5xy^{2}z+3x^{2}yz-xyz+1;B=7x^{2}yz-5xy^{2}z+3xyz^{2}-2$

a) Tìm đa thức C sao cho A - C = B

b) Tìm đa thức D sao cho A + D = B

c) Tìm đa thức E sao cho E - A = B

Hướng dẫn giải:

- Áp dụng quy tắc chuyển vế đổi dấu:

a) Đa thức C = A - B

b) Đa thức D = B - A

c) Đa thức E = A + B

- Thu gọn đa thức

Bài giải:

a) A - C = B

$\Rightarrow C = A - B=(7xyz^{2}-5xy^{2}z+3x^{2}yz-xyz+1)-(7x^{2}yz-5xy^{2}z+3xyz^{2}-2)$ $\Rightarrow C = A - B=(7xyz^{2}-5xy^{2}z+3x^{2}yz-xyz+1)-(7x^{2}yz-5xy^{2}z+3xyz^{2}-2)$

$\Rightarrow C=7xyz^{2}-5xy^{2}z+3x^{2}yz-xyz+1-7x^{2}yz+5xy^{2}z-3xyz^{2}+2$ $\Rightarrow C=7xyz^{2}-5xy^{2}z+3x^{2}yz-xyz+1-7x^{2}yz+5xy^{2}z-3xyz^{2}+2$

$\Rightarrow C=4xyz^{2}-4x^{2}yz-xyz+3$ $\Rightarrow C=4xyz^{2}-4x^{2}yz-xyz+3$

b) A + D = B

$\Rightarrow D = B - A=(7x^{2}yz-5xy^{2}z+3xyz^{2}-2)-(7xyz^{2}-5xy^{2}z+3x^{2}yz-xyz+1)$ $\Rightarrow D = B - A=(7x^{2}yz-5xy^{2}z+3xyz^{2}-2)-(7xyz^{2}-5xy^{2}z+3x^{2}yz-xyz+1)$

$\Rightarrow D=7x^{2}yz-5xy^{2}z+3xyz^{2}-2-7xyz^{2}+5xy^{2}z-3x^{2}yz+xyz-1$ $\Rightarrow D=7x^{2}yz-5xy^{2}z+3xyz^{2}-2-7xyz^{2}+5xy^{2}z-3x^{2}yz+xyz-1$

$\Rightarrow D=4x^{2}yz-4xyz^{2}+xyz-3$ $\Rightarrow D=4x^{2}yz-4xyz^{2}+xyz-3$

C) E - A = B

$\Rightarrow E = A + B=(7xyz^{2}-5xy^{2}z+3x^{2}yz-xyz+1)+(7x^{2}yz-5xy^{2}z+3xyz^{2}-2)$ $\Rightarrow E = A + B=(7xyz^{2}-5xy^{2}z+3x^{2}yz-xyz+1)+(7x^{2}yz-5xy^{2}z+3xyz^{2}-2)$

$\Rightarrow E=7xyz^{2}-5xy^{2}z+3x^{2}yz-xyz+1+7x^{2}yz-5xy^{2}z+3xyz^{2}-2$ $\Rightarrow E=7xyz^{2}-5xy^{2}z+3x^{2}yz-xyz+1+7x^{2}yz-5xy^{2}z+3xyz^{2}-2$

$\Rightarrow E=10xyz^{2}-10xy^{2}z+10x^{2}yz-xyz-1$ $\Rightarrow E=10xyz^{2}-10xy^{2}z+10x^{2}yz-xyz-1$

Bài 1.22

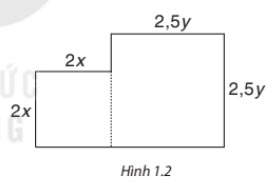
Từ một nửa miếng bìa, người ta cắt ra hai hình tròn có bán kính x cm và y xm. Tìm biểu thức biểu thị diện tích phần còn lại của miếng bìa, nếu miếng bìa có hình dạng gồm hai hình vuông ghép lại và có kích thước (cm) như hình 1.2. Biểu thức đó có phải là một đa thức không? Nếu phải thì đó là đa thức bậc mấy?

Bài 1.22

Hướng dẫn:

- Viết biểu thức biểu thị phần diện tích còn lại của miếng bìa:

Diện tích phần còn lại = Tổng diện tích hình vuông - tổng diện tích hình tròn

- Thu gọn biểu thức

- Nếu biểu thức đó là đa thức, ta xác định bậc của đa thức đó

Bài giải:

Diện tích của miếng bìa là: $2x\times 2x+2,5y\times 2,5y=4x^{2}+6,25y^{2}(cm^{2})$ $2x\times 2x+2,5y\times 2,5y=4x^{2}+6,25y^{2}(cm^{2})$

Diện tích hai hình tròn là: $x\times x\times 3,14+y\times y\times 3,14=3,14x^{2}+3,14y^{2}(cm^{2})$ $x\times x\times 3,14+y\times y\times 3,14=3,14x^{2}+3,14y^{2}(cm^{2})$

Dện tích phần còn lại là: $4x^{2}+6,25y^{2}-3,14x^{2}-3,14y^{2}=0,86x^{2}+3,11y^{2}(cm^{2})$ $4x^{2}+6,25y^{2}-3,14x^{2}-3,14y^{2}=0,86x^{2}+3,11y^{2}(cm^{2})$

Biểu thức $0,86x^{2}+3,11y^{2}$ $0,86x^{2}+3,11y^{2}$ là đa thức bậc 2