Toán 8 Bài 12: Hình bình hành Giải Toán 8 Kết nối tri thức trang 57, 58, 59, 60, 61

Giải bài tập Toán lớp 8 Bài 12: Hình bình hành với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 8 Tập 1 Kết nối tri thức với cuộc sống trang 57, 58, 59, 60, 61. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 8 Bài 12 chi tiết phần luyện tập, bài tập, đồng thời còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của Bài 12 Chương III: Tứ giác. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Phần Luyện tập

Luyện tập 1 trang 58 Toán 8 tập 1

Cho tam giác ABC. Từ một điểm M tùy ý trên cạnh BC, kẻ đường thẳng song song với AB, cắt cạnh AC tại N và kẻ đường thẳng song song với AC, cắt cạnh AB tại P. Gọi I là trung điểm của đoạn NP. Chứng minh rằng I cũng là trung điểm của đoạn AM.

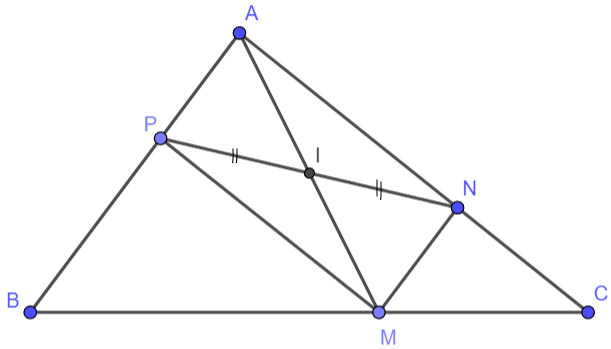
Ta có MN // AB hay MN // AP

MP // AC hay MP // AN

Xét tứ giác ANMP có MN // AP và MP // AN

Suy ra ANMP là hình bình hành

Mà I là trung điểm của đường chéo NP

Suy ra I cũng là trung điểm của đường chéo AM (đpcm)

Luyện tập 2 trang 60 Toán 8 tập 1

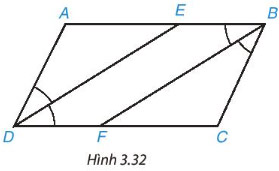
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E và tia phân giác của góc B cắt CD tại F (H.3.32)

a) Chứng minh hai tam giác ADE và CBF là những tam giác cân, bằng nhau

b) Tứ giác DEBF là hình gì? Tại sao?

Bài giải

a) Chứng minh hai tam giác ADE và CBF là những tam giác cân, bằng nhau

*) Vì ABCD là hình bình hành nên \(\widehat{ADC}=\widehat{ABC}\)

Do DE và BF lần lượt là tia phân giác của góc \(\widehat{ADC}\) và \(\widehat{ABC}\)

Suy ra \(\widehat{ADE}=\widehat{EDC}=\widehat{ABF}=\widehat{CBF}\)

Mặt khác: ABCD là hình bình hành nên AB // DC, suy ra \(\widehat{AED}=\widehat{EDC}\) (hai góc so le trong)

Do đó: \(\widehat{AED}=\widehat{ADE}\)

Xét tam giác ADE có \(\widehat{AED}=\widehat{ADE}\) (cmt). Suy ra, tam giác ADE là tam giác cân tại A

Chứng minh tương tự, ta có tam giác CBF là tam giác cân tại C

*) Xét tam giác ADE và tam giác CBF ta có:

\(\widehat{ADE}=\widehat{CBF}\)

AD = CB

\(\widehat{A}=\widehat{C}\)

Do đó \(\Delta ADE=\Delta CBF\) (g.c.g)

b) Tứ giác DEBF là hình gì? Tại sao?

Ta có \(\Delta ADE=\Delta CBF\) (cmt)

Suy ra DE = BF (hai cạnh tương ứng)

Lại có \(\widehat{EDC}=\widehat{CBF}\) (cmt) và \(\widehat{CFB}=\widehat{CBF}\) (vì tam giác BCF cân tại C)

Suy ra \(\widehat{EDC}=\widehat{CFB}\)

Mà hai góc này ở vị trí đồng vị. Suy ra DE // BF

Xét tứ giác DEBF có EB // DF (vì AB // DC) và DE // BF (cmt)

Suy ra DEBF là hình bình hành.

Luyện tập 3 trang 61 Toán 8 tập 1

Cho hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB. Gọi A', B' là các điểm sao cho O là trung điểm của AA', BB'. Chứng minh rằng A'B' = AB và đường thẳng A'B' song song với đường thẳng AB.

Bài giải

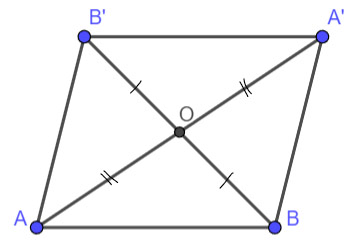
Xét tứ giác ABA'B' ta có: AA' và BB' là hai đường chéo và O là trung điểm của mỗi đường

Suy ra ABA'B' là hình bình hành (dấu hiệu nhận biết)

Do đó A'B' = AB và A'B' // AB (tính chất hình bình hành)

Phần Bài tập

Bài 3.13 trang 61 Toán 8 tập 1

Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Vì sao?

a) Hình thang có hai cạnh bên song song là hình bình hành

b) Hình thang có hai cạnh bên bằng nhau là hình bình hành

c) Tứ giác có hai cạnh đối nào cũng song song là hình bình hành

Bài giải:

a) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)

b) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

c) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)

Bài 3.14 trang 61 Toán 8 tập 1

Tính các góc còn lại của hình bình hành ABCD trong Hình 3.35.

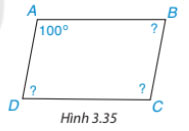
Bài giải:

\(\widehat{C}=\widehat{A}=100^{\circ}\)

\(\widehat{D}=\widehat{B}=180^{\circ}-\widehat{A}=180^{\circ}-100^{\circ}=80^{\circ}\)

Bài 3.15 trang 61 Toán 8 tập 1

Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh BF = DE.

Bài giải:

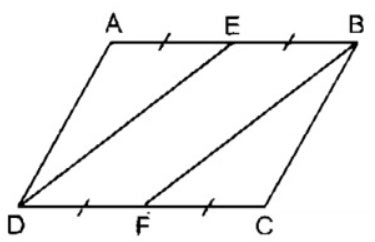
Ta có: AB = CD (tính chất hình bình hành)

EB = \(\frac{1}{2}\) AB (gt)

FD = \(\frac{1}{2}\) CD (gt)

Suy ra: EB = FD (1)

Mà AB // CD (gt)

⇒ BE // FD (2)

Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

⇒ DE = BF (tính chất hình bình hành)

Bài 3.16 trang 61 Toán 8 tập 1

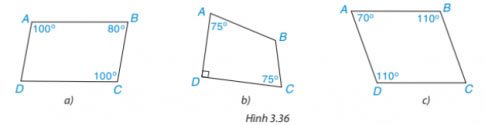
Trong mỗi trường hợp sau đây, tứ giác nào là hình bình hành, tứ giác nào không là hình bình hành? Vì sao?

Bài giải:

a) \(\widehat{D}=80^{\circ}\), ABCD là hình bình hành vì có các góc đối bằng nhau.

b) \(\widehat{B}=120^{\circ}\), ABCD không là hình bình hành vì có cặp góc đối không bằng nhau.

c) \(\widehat{C}=70^{\circ}\), ABCD là hình bình hành vì có các góc đối bằng nhau.

Bài 3.17 trang 61 Toán 8 tập 1

Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh rằng:

a) Hai tứ giác AEFD, AECF là những hình bình hành

b) EF = AD, AF = EC

Bài giải:

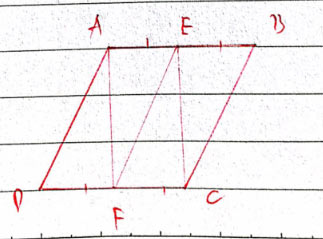
a) Xét tứ giác AECF có

AE//CF

AE=CF

Do đó: AECF là hình bình hành

Xét tứ giác AEFD có

AE//DF

AE=DF

Do đó: AEFD là hình bình hành

b) EF = AD do AEFD là hình bình hành

AF = EC do AECF là hình bình hành

Bài 3.18 trang 61 Toán 8 tập 1

Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh \(\Delta OAM=\Delta OCN\). Từ đó suy ra tứ giác MBND là hình bình hành

Bài giải:

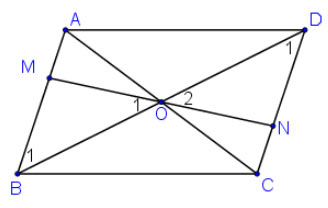
Xét tam giác OAM và OCN ta có:

\(\widehat{AOM}=\widehat{CON}\) (đối đỉnh)

OA = ON

\(\widehat{OAM}=\widehat{OCN}\) (so le trong)

Suy ra, \(\Delta OAM=\Delta OCN\) (g.c.g) do đó AM = CN

Lại có AB = CD, suy ra MB = ND

Ta có : MB = ND, MB// ND \(\Rightarrow\) tứ giác MBND là hình bình hành