Toán 8 Bài tập cuối chương X Giải Toán 8 Kết nối tri thức tập 2 trang 123, 124

Giải Toán 8 Bài tập cuối chương X là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Kết nối tri thức với cuộc sống tập 2 trang 123, 124.

Giải bài tập Toán 8 Kết nối tri thức tập 2 trang 123, 124 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài tập cuối chương X: Một số hình khối trong thực tiễn. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 8 Kết nối tri thức Tập 2 trang 123 - Trắc nghiệm

Bài 10.15

Trung đoạn của hình chóp tam giác đều trong Hình 10.34 là:

A. SB
B. SH
C. SI
D. HI

Đáp án: C

Bài 10.16

Đáy của hình chóp tứ giác đều là:

A. Hình vuông
B. Hình bình hành
C. Hình thoi
D. Hình chữ nhật

Đáp án: A

Bài 10.17

Diện tích xung quanh của hình chóp tam giác đều bằng:

A. Tích của nửa chu vi đáy và chiều cao của hình chóp
B. Tích của nửa chu vi và trung đoạn
C. Tích của chu vi đáy và trung đoạn
D. Tổng của chu vi đáy và trung đoạn

Đáp án: B

Bài 10.18

Một hình chóp tam giác đều có chiều cao h, thể tích V. Diện tích đáy S là:

\(A. S=\frac{h}{V}\)

\(B. S=\frac{V}{h}\)

\(C. S=\frac{3V}{h}\)

\(D. S=\frac{3h}{V}\)

Đáp án: C

Giải Toán 8 Kết nối tri thức Tập 2 trang 123, 124 - Tự luận

Bài 10.19

Gọi tên đỉnh, cạnh bên, cạnh đáy, đường cao và một trung đoạn của hình chóp tam giác đều, hình chóp tứ giác đều

Lời giải:

Bài 10.20

Tính diện tích xung quanh của hình chóp tam giác đều, hình chóp tứ giác đều trong Hình 10.36

Lời giải:

- Nửa chu vi của ABC là: \((12+12+12):2=18\) (m)

- Xét tam giác HBD vuông tại H, có:

\(HD^{2}=BD^{2}-BH^{2}=8^{2}-6^{2}\)

\(HD=2\sqrt{7}\)

=> Diện tích xung quanh của hình chóp tam giác đều là \(Sxq=p.d=18.2\sqrt{7}=36\sqrt{7}\) (\(m^{2}\)

Nửa chu vi tam giác ABCD là: \((10.4):2=20\)

- Xét tam giác SHD vuông tại H, có:

\(SH^{2}=SD^{2}-HD^{2}=12^{2}-6^{2}\)

\(SH=\sqrt{119}\)

=> Diện tích xung quanh của hình chóp tứ giác đều là \(Sxq=p.d=20.\sqrt{119}=20\sqrt{119}\) (\(m^{2}\))

Bài 10.21

Tính thể tích của hình chóp tứ giác đều, biết chiều cao bằng 9 cm và chu vi đáy bằng 12 cm

Lời giải:

Có chu vi đáy bằng 12 cm => Cạnh của đáy là: \(12:4=3\) (cm) (vì đáy của hình chóp tứ giác đều là hình vuông)

- Diện tích đáy là: \(3.3=9\) (\(cm^{2}\))

- Thể tích hình chóp là:

\(V=\frac{1}{3}\cdot S\cdot h=\frac{1}{3}\cdot 9\cdot 9=27\) (\(cm^{3}\))

Bài 10.22

Từ một khúc gỗ hình lập phương cạnh 30 cm, người ta cắt đi một phần gỗ để được phần còn lại là một hình chóp tứ giác đều có đáy là hình vuông cạnh 30 cm và chiều cao của hình chóp cũng bằng 30 cm. Tính thể tích của phần gỗ bọ cắt đi

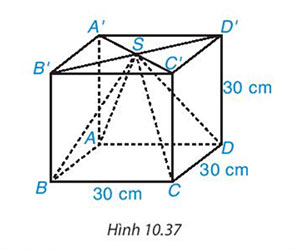
Lời giải:

a) Diện tích mặt đáy của hình chóp tứ giác đều ABCD là: \(30.30=900\) (\(cm^{2}\))

- Thể tích hình chóp là:

\(V=\frac{1}{3}\cdot S\cdot h=\frac{1}{3}\cdot 900\cdot 30=9000\) (\(cm^{3}\))

- Thể tích hình lập phương là \(V=30.30.30=27000\) (\(cm^{3}\))

Vậy thể tích phân gỗ bị cắt đi là \(V=27000-9000=18000\) (\(cm^{3}\))

Bài 10.23

Một khối gỗ gồm đế là hình lập phương cạnh 9 cm và một hình chóp tứ giác đều. Tính thể tích khối gỗ.

Bài 10.24

Bạn Trang cắt miếng bìa hình tam giác đều cạnh dài 20 cm và gấp lại theo các dòng kẻ (nét đứt) để được hình chóp tam giác đều. Tính diện tích xung quanh của hình chóp tam giác đều tạo thành. Cho biết \(\sqrt{75}\) ≈ \(8,66\).