Toán 8 Bài 34: Ba trường hợp đồng dạng của hai tam giác Giải Toán 8 Kết nối tri thức tập 2 trang 83, 84, 85, 86, 87, 88, 89, 90

Toán 8 Bài 34: Ba trường hợp đồng dạng của hai tam giác là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Kết nối tri thức với cuộc sống tập 2 trang 83, 84, 85, 86, 87, 88, 89, 90.

Giải Toán 8 Kết nối tri thức tập 2 trang 83 → 90 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 34 Chương IX: Tam giác đồng dạng. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 8 Kết nối tri thức Tập 2 trang 90

Bài 9.5

Khẳng đinh nào sau đây chứng tỏ hai tam giác đồng dạng?

a) Ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia

b) Hai cạnh của tam giá này tỉ lệ với hai cạnh của tam giác kia và có một cặp góc bằng nhau

c) Hai góc của tam giác này bằng hai góc của tam giác kia

d) Hai cạnh của tam giác này bằng hai cạnh của tam giác kia

Lời giải:

Bài 9.6

Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4cm, 8cm và 10cm. Tam giác thứ hai có chu vi là 33cm. Độ dài ba cạnh của tam giác thứ hai là bộ ba nào sau đây?

a) 6cm, 12cm, 15cm
b) 8cm, 16cm, 20cm
c) 6cm, 9cm, 18cm
d) 8cm, 10cm, 15cm

Lời giải:

Có chu vi tam giác là: a + b + c = 33cm => loại phương án b

Xét phương án a, nhận thấy \(\frac{4}{6}=\frac{8}{12}=\frac{10}{15}=\frac{2}{3}\)

=> phương án a là phương án đúng.

Bài 9.7

Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng \(\Delta A'B'C'\) ~ \(\Delta ABC\)

Chứng minh rằng \(\frac{A'M'}{AM}=\frac{B'N'}{BN}=\frac{C'P'}{CP}\)

Lời giải:

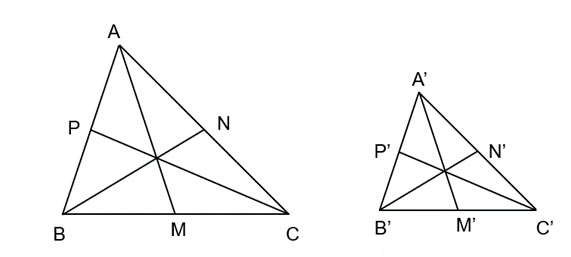
Vì \(\Delta A'B'C'\) ~ \(\Delta ABC\)

=> \(\Delta A'M'B'\) ~ \(\Delta AMB\)

=> \(\frac{A'M'}{AM}=\frac{A'B'}{AB}\) (1)

Vì \(\Delta A'B'C'\) ~ \(\Delta ABC\)

=> Vì \(\Delta A'B'N'\) ~ \(\Delta ABN\)

=> \(\frac{B'N'}{BN}=\frac{A'B'}{AB}\) (2)

Từ (1) và (2) => \(\frac{A'M'}{AM}=\frac{B'N'}{BN}\) (3)

Vì \(\Delta A'B'C'\) ~ \(\Delta ABC\)

=> Vì \(\Delta A'C'P'\) ~ \(\Delta ACP\)

=> \(\frac{C'P'}{CP}=\frac{A'C'}{AC}\) (4)

Vì \(\Delta A'B'C'\) ~ \(\Delta ABC\)

=> \(\Delta A'M'C'\) ~ \(\Delta AMC\)

=> \(\frac{A'M'}{AM}=\frac{A'C'}{AC}\) (5)

Từ (4) và (5) => \(\frac{C'P'}{CP}=\frac{A'M'}{AM}\) (6)

Từ (3) và (6) => \(\frac{A'M'}{AM}=\frac{B'N'}{BN}=\frac{C'P'}{CP}\)

Bài 9.8

Cho tam giác ABC có \(AB=12cm\), \(AC=5cm\). Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho \(AM=10cm\), \(AN=8cm\). Chứng minh rằng \(\Delta ABC\) ~ \(\Delta ANM\)

Lời giải:

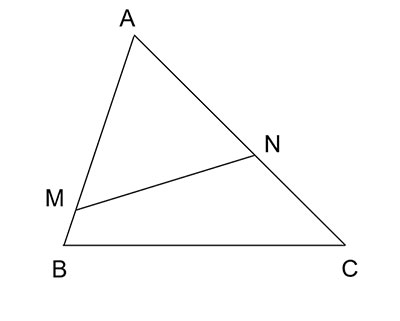
Có \(AB=12cm\) , \(AN=8cm\) => \(\frac{AN}{AB}=\frac{8}{12}=\frac{2}{3}\)

\(AC=5cm\), \(AM=10cm\) => \(\frac{AM}{AC}=\frac{10}{15}=\frac{2}{3}\)

=> \(\frac{AN}{AB}=\frac{AM}{AC}\)

- Xét hai tam giác ABC và tam giác ANM, có

\(\frac{AN}{AB}=\frac{AM}{AC}\), góc A chung

=> ΔABC ~ ΔANM' (c.g.c)

Bài 9.9

Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \(\widehat{ABN}=\widehat{ACM}\)

a) Chứng minh rằng ΔABN ~ ΔACM

b) Gọi I là giao điểm của BN và CM. Chứng minh rằng \(IB.IN=IC.IM\)

Lời giải:

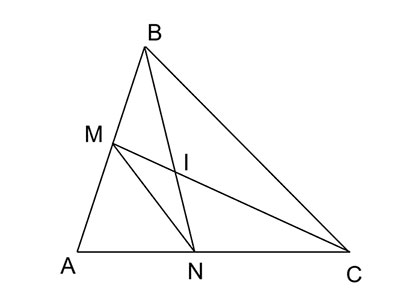
a) Xét tam giác ABN và tam giác ACM

có góc A chung, \(\widehat{ABN}=\widehat{ACM}\)

=> ΔABN ~ ΔACM

b) Có ΔABN ~ ΔACM

\(\widehat{ANB}=\widehat{AMC}\)

Có \(\widehat{ANB}+\widehat{CNB}=180°\)

\(\widehat{AMC}+\widehat{BMC}=180°\)

=> \(\widehat{CNB}=\widehat{BMC}\)

Xét tam giác IBM và tam giác ICN

Có \(\widehat{CNB}=\widehat{BMC}\) và \(\widehat{IBM}=\widehat{ICN}\)

=> ΔIBM ~ ΔICN (g.g)

=> \(\frac{IB}{IC}=\frac{IM}{IN}\)

=> \(IB.IN=IC.IM\)

Bài 9.10

Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3m và 2m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25), hãy tính độ cao h của điểm đó so với mặt đất

Lời giải:

Theo đề bài, ta có hình vẽ:

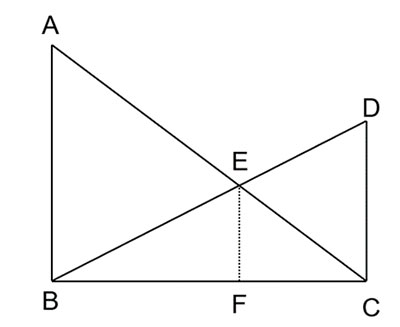
- Có AB // CD

=> \(\widehat{BAC}=\widehat{DCA}\) (2 góc so le trong)

\(\widehat{BDC}=\widehat{ABD}\) (2 góc so le trong)

- Xét hai tam giác ABE và tam giác CDE, có \(\widehat{BAC}=\widehat{DCA}\), \(\widehat{BDC}=\widehat{ABD}\)

=> ΔABE ~ ΔCDE

=> \(\frac{CD}{AB}=\frac{CE}{AE}=\frac{2}{3}\)

=> \(\frac{CE}{AE}=\frac{2}{3}\) => \(\frac{CE}{CA}=\frac{2}{5}\)

- Xét hai tam giác CEF và tam giác CAB có EF // AB

=> ΔCEF ~ ΔCAB (theo định lý)

=> \(\frac{FE}{AB}=\frac{CE}{CA}=\frac{2}{5}\)

=> \(\frac{FE}{AB}=\frac{2}{5}\) => \(\frac{FE}{3}=\frac{2}{5}\) => \(EF=frac{6}{5}=1,2\) (m)

Vậy độ cao h là 1,2 m