Toán 8 Bài 1: Đơn thức và đa thức nhiều biến Giải Toán 8 Chân trời sáng tạo trang 6, 7, 8, 9, 10, 11

Giải Toán lớp 8 trang 11 tập 1 Chân trời sáng tạo giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần Hoạt động khởi động, thực hành và 5 bài tập thuộc bài 1 Đơn thức và đa thức nhiều biến được nhanh chóng và dễ dàng hơn.

Toán 8 Chân trời sáng tạo tập 1 trang 6, 7, 8, 9, 10, 11 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 8. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 8 Đơn thức và đa thức nhiều biến trang 11 Chân trời sáng tạo mời các bạn cùng theo dõi.

Phần Hoạt động khởi động

Hình bên là bản vẽ sơ lược nền của một ngôi nhà (các kích thước tính theo m).

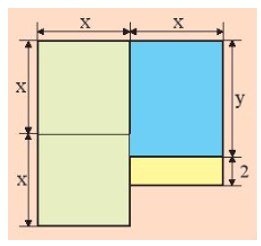
Có thể biểu thị diện tích của nền nhà bằng một biểu thức chứa x và y không? Nếu có, trong biểu thức đó chứa các phép tính nào?

Lời giải:

Có thể biểu thị diện tích của nền nhà bằng một biểu thức chứa x và y.

Ta chia nền nhà thành các hình chữ nhật ABCD, BEFG, GHKF như hình vẽ dưới đây.

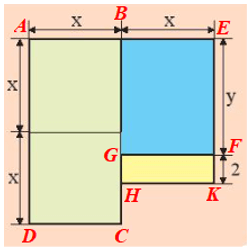
Biểu thức biểu thị diện tích hình chữ nhật ABCD là:

(x + x).x = 2x.x = 2x² (m²).

Biểu thức biểu thị diện tích hình chữ nhật BEFG là: xy (m²).

Biểu thức biểu thị diện tích hình chữ nhật GHKF là: 2x (m²).

Diện tích nền nhà là tổng diện tích của các hình chữ nhật nên biểu thức biểu thị diện tích nền nhà là:

2x² + xy + 2x (m²).

Trong biểu thức trên có chứa phép cộng, phép nhân.

Phần Thực hành

Thực hành 1 trang 7 Toán 8 tập 1

Cho các biểu thức sau:

\(ab-\pi r^{2};\frac{4\pi r^{3}}{3};\frac{p}{2\pi };x-\frac{1}{y};0;\frac{1}{\sqrt{2}};x^{3}-x+1\)

Trong các biểu thức trên hãy chỉ ra:

a) Các đơn thức

b) Các đa thức và số hạng tử của chúng.

Gợi ý đáp án

a) Các đơn thức: \(\frac{4\pi r^{3}}{3};\frac{p}{2\pi };0;\frac{1}{\sqrt{2}}\)

b) Các đa thức:

- Các đơn thức ở câu a) đều có 1 hạng tử

- Đa thức \(ab-\pi r^{2}\) có 2 hạng tử, đa thức \(x^{3}-x+1\) có 3 hạng tử

Thực hành 2 trang 9 Toán 8 tập 1

Thu gọn các đơn thức sau đây. Chỉ ra hệ số và bậc của chúng.

a) \(12xy^{2}x\)

b) \(-y(2x)y\)

c) \(x^{3}yx\)

d) \(5x^{2}y^{3}z^{4}y\)

Gợi ý đáp án

a) \(12xy^{2}x=12x^{2}y^{2}\) có hệ số là 12, bậc bằng 4

b) \(-y(2x)y=-2y^{2}z\) có hệ số là -2, bậc bằng 3

c) \(x^{3}yx=x^{4}y\) có hệ số là 1, bậc bằng 5

d) \(5x^{2}y^{3}z^{4}y=5x^{2}y^{4}z^{4}\) có hệ số là 5, bậc bằng 10

Thực hành 3 trang 10 Toán 8 tập 1

Mỗi cặp đơn thức sau có đồng dạng không? Nếu có, hãy tìm tổng và hiệu của chúng.

a) xy và -6xy

b) 2xy và \(xy^{2}\)

c) \(-4yzx^{2}\)và \(4x^{2}yz\)

Gợi ý đáp án

a) xy và -6xy là hai đơn thức đồng dạng vì có hệ số khác 0 và cùng phần biến là xy

\(xy + (-6xy) = -5xy\)

\(xy - (-6xy) = 7xy\)

b) 2xy và \(xy^{2}\) không phải hai đơn thức đồng dạng vì có phần biến khác nhau

c) \(-4yzx^{2}\) và \(4x^{2}y\) là hai đơn thức đồng dạng vì có hệ số khác 0 và cùng phần biến là x²yz

Thực hành 4 trang 10 Toán 8 tập 1

Thu gọn và tìm bậc của mỗi đa thức sau:

\(a)A=x-2y+xy-3x+y^{2}\)

\(b)B=xyz-x^{2}y+xz-\frac{1}{2}xyz+\frac{1}{2}xz\)

Gợi ý đáp án

\(a)A=x-2y+xy-3x+y^{2}=-2x-2y+xy+y^{2}\) có bậc bằng 2

\(b)B=xyz-x^{2}y+xz-\frac{1}{2}xyz+\frac{1}{2}x\)

\(z=\frac{1}{2}xyz-x^{2}y+\frac{3}{2}xz\) có bậc bằng 3

Thực hành 5 trang 10 Toán 8 tập 1

Tính giá trị của đa thức \(A=3x^{2}y-5xy-2x^{2}y-3xy\) tại \(x=3;y=\frac{1}{2}\)

Gợi ý đáp án

\(A=3x^{2}y-5xy-2x^{2}y-3xy=x^{2}y-8xy\)

Thay \(x=3;y=\frac{1}{2}\) vào đơn thức A ta có:

\(3^{2}\times \frac{1}{2}-8\times  3\times  \frac{1}{2}=-\frac{15}{2}\)

\(-4yzx^{2}+4x^{2}yz=0\)

\(-4yzx^{2}-4x^{2}yz=-8x^{2}yz\)

Phần Bài tập

Bài tập 1 trang 11 Toán 8 tập 1

Chỉ ra các đơn thức, đa thức trong các biểu thức sau:

\(-3;2z;\frac{1}{3}xy+1;-10x^{2}yz;\frac{4}{xy};5x-\frac{z}{2};1+\frac{1}{y}\)

Gợi ý đáp án

Các đơn thức: \(-3;2z;-10x^{2}yz\)

Bài tập 2 trang 11 Toán 8 tập 1

Thu gọn các đơn thức sau. Chỉ ra hệ số, phần biến và bậc của mỗi đơn thức.

\(5xyx; -xyz\frac{2}{3}y;-2x^{2}(-\frac{1}{6})x\)

Gợi ý đáp án

\(5xyx=5x^{2}y\) có hệ số là 5, phần biến là \(x^{2}y\), bậc bằng 3

\(-xyz\frac{2}{3}y=-\frac{2}{3}xy^{2}z\) có hệ số là \(-\frac{2}{3}\), phần biến là \(xy^{2}z\), bậc bằng 4

\(-2x^{2}(-\frac{1}{6})x=\frac{1}{3}x^{3}\)có hệ số là \(\frac{1}{3}\), phần biến là \(x^{3}\), bậc bằng 3

Bài tập 3 trang 11 Toán 8 tập 1

Thu gọn và tìm bậc của mỗi đa thức sau:

a) \(M = x - 3 - 4y + 2x - y\)

b) \(N=-x^{2}t+13t^{3}+xt^{2}+5t^{3}-4\)

Gợi ý đáp án

a) \(M = x - 3 - 4y + 2x - y = 3x -5y -3\) có bậc bằng 1

b) \(N=-x^{2}t+13t^{3}+xt^{2}+5t^{3}-4\)

\(=-x^{2}t+18t^{3}+xt^{2}-4\) có bậc bằng 3

Bài tập 4 trang 11 Toán 8 tập 1

Tính giá trị của đa thức \(P=3xy^{2}-6xy+8xz+xy^{2}-10xz\) tại \(x=-3;y=-\frac{1}{2};z=3\)

Gợi ý đáp án

\(P=3xy^{2}-6xy+8xz+xy^{2}-10xz\)

\(=4xy^{2}-6xy-2xz\)

Thay \(x=-3;y=-\frac{1}{2};z=3\) vào P ta có:

\(4\times (-3)\times (-\frac{1}{2})^{2}-6\times (-2)\times (-\frac{1}{2})-2\times (-3)\times 3=9\)

Bài tập 5 trang 11 Toán 8 tập 1

Viết biểu thức biểu thị thể tích V và diện tích xung quanh S của hình hộp chữ nhật trong Hình 5. Tính giá trị của V, S khi x = 4 cm, y = 2 cm và z = 1 cm

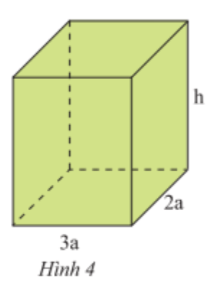
Gợi ý đáp án

\(V=2x\times 4y\times 2z=24xyz(cm^{3})\)

\(S=2\times 2z\times (3x+4y)=12xz+16yz(cm^{2})\)

Thay x = 4, y = 2, z = 1 vào V ta có: \(24\times 4\times 2\times 1=192(cm^{3})\)

Thay x = 4, y = 2, z = 1 vào S ta có: \(12\times 4\times 1+16\times 2\times 1=80(cm^{2})\)