Toán 8 Bài 4: Hình bình hành - Hình thoi Giải Toán 8 Chân trời sáng tạo trang 73, 74, 75, 76, 77, 78, 79, 80, 81

Toán lớp 8 tập 1 trang 73, 74, 75, 76, 77, 78, 79, 80, 81 Chân trời sáng tạo là tài liệu vô cùng hữu ích mà Eballsviet.com muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 8 tham khảo.

Giải Toán 8 Chân trời sáng tạo Bài 4 Hình bình hành - Hình thoi được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 80, 81. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán lớp 8 tập 1 chương III Bài 4 Hình bình hành - Hình thoi Chân trời sáng tạo, mời các bạn cùng theo dõi tại đây.

Toán 8 Tập 1 trang 80, 81 Chân trời sáng tạo

Bài tập 1

Cần thêm một điều kiện gì để mỗi tứ giác trong Hình 19 trở thành hình bình hành?

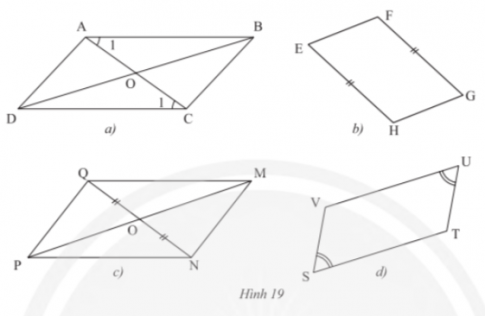
Gợi ý đáp án

a) AB = CD

b) EH // FG

c) OM = OP

d) \(\widehat{V}=\widehat{T}\)

Bài tập 2

Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K (Hình 21)

a) Chứng minh tứ giác AHCK là hình bình hành

b) Gọi I là trung điểm của HK. Chứng minh IB = ID

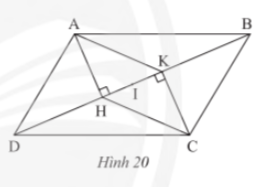
Gợi ý đáp án

a) Xét tam giác vuông DKC và BHA ta có:

DC = AB( hbh ABCD)

\(\widehat{CDK}=\widehat{ABH}\) (hbh ABCD, AB//DC)

Suy ra \(\Delta   DKC=\Delta   BHA\)( ch-gn)

=> CK=AH

Ta có : AH \(\perp\) DB

CK \(\perp\) DB

=> CK//AH

Xét tứ giác AKCH có CK//AH (cmt)

CK=AH (cmt)

=> AKCH là hình bình hành (dấu hiệu 3)

b) AKCH là hình bình hành suy ra AC và HK cắt nhau tại trung điểm của mỗi đường , do đó I là trung điểm của AC

ABCD là hình bình hành suy ra AC và BD cắt nhau tại trung điểm của mỗi đường , do đó I là trung điểm của BD hay IB = ID

Bài tập 3

Cho hình bình hành ABCD. Gọi E là trung điểm AD, F là trung điểm của BC.

a) Chứng minh rằng tứ giác EBFD là hình bình hành.

b) Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Chứng minh rằng ba điểm E, O, F thẳng hàng

Gợi ý đáp án

a) Ta có :

ED= \(\frac{1}{2}AD\) (E là trung điểm của AD)

BF=\(\frac{1}{2}BC\) (F là trung điểm của BC)

Và AD=BC (ABCD là hình bình hành)

⇒ED=BF

Mà ED // BF (AD // BC, E∈AD;F∈BC)

Do đó tứ giác EBFD là hình bình hành.

b) O là tâm đối xứng của hình bình hành ABCD ⇒Olà trung điểm của BD

Hình bình hành EBFD có O là trung điểm của BD ⇒O là trung điểm của EF.

⇒O∈EF

Vậy E, O, F thẳng hàng.

Bài tập 4

Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a) Chứng minh rằng DE // BF.

b) Tứ giác DEBF là hình gì?

Gợi ý đáp án

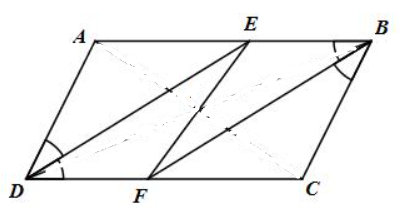
a) Ta có \(\widehat{ABC}=\widehat{ADC}\) (tứ giác ABCD là hình bình hành)

\(\widehat{ABF}=\frac{\widehat{ABC}}{2}\) (BF là tia phân giác của \(\widehat{ABC}\)) và \(\widehat{CDE}=\frac{\widehat{ADC}}{2}\) (DE là tia phân giác của \(\widehat{ADC}\))

⇒\(\widehat{ABF}=\widehat{CDE}\)

Mà \(\widehat{ADE}=\widehat{CDE}\)(hai góc so le trong và AB // CD)

Nên \(\widehat{ABF}=\widehat{AED}\)

Lại có \(\widehat{ABF};\widehat{AED}\) là hai góc đồng vị

⇒DE//BF

b) Tứ giác DEBF có DE // BF và EB // DF (AB // CD)

Do đó tứ giác DEBF là hình bình hành (dấu hiệu nhận biết)

Bài tập 5

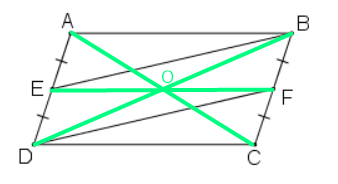
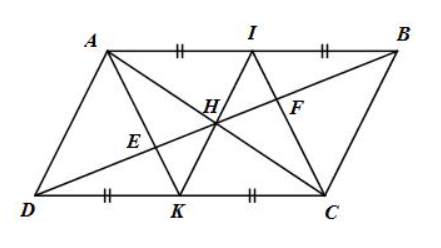
Cho hình bình hành ABCD. Gọi I, K lần lượt là trung điểm của các cạnh AB và CD, E và F là giao điểm của AK và CI với BD.

a) Chứng minh tứ giác AKCI là hình bình hành.

b) Chứng minh rằng DE = EF = FB.

Gợi ý đáp án

a) Ta có:

AI=\(\frac{1}{2}AB\) (I là trung điểm của AB),

CK=\(\frac{1}{2}CD\) (K là trung điểm của CD)

Và AB=CD(ABCD là hình bình hành)

⇒AI=CK

Mà AI // CK (AB//CD,I∈AB,K∈CD)

Do đó tứ giác AICK là hình bình hành.

b) ΔABEcó I là trung điểm của AB và IF//AE

Nên F là trung điểm của EB ⇒BF=EF (1)

ΔDCFcó EK // FC và K là trung điểm của CD

Nên E là trung điểm của DF ⇒DE=EF (2)

Từ (1) và (2) suy ra DE=EF=BF

Bài tập 6

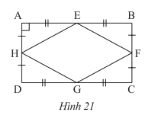
Cho hình 21. Chứng minh rằng tứ giác EFGH là hình thoi.

Gợi ý đáp án

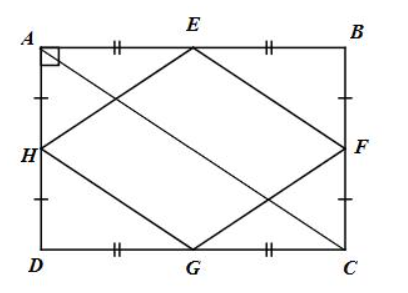
E, F lần lượt là trung điểm của AB và BC

⇒EF là đường trung bình của tam giác ABC

⇒EF//AC và EF=\(\frac{1}{2}AC\) (1)

H, G lần lượt là trung điểm của AD và DC

⇒HG là đường trung bình của tam giác ACD

⇒HG//ACvà HG=\(\frac{1}{2}AC\) (2)

Từ (1) và (2) ⇒EF//HGvà EF=HG

Vậy tứ giác EFGH là hình bình hành.

Tứ giác ABCD có AB=CDvà AD=BC⇒ Tứ giác ABCD là hình bình hành.

Mà \(\widehat{BAD}=90^{\circ}\) ⇒ ABCD là hình chữ nhật.

Xét ΔEBFvà ΔCGFcó :

EB=EC(gt)

BF=FC(gt)

\(\widehat{EBF}=\widehat{GCF}(=90^{\circ})\)

⇒ΔEBF=ΔGCF(c.g.c)⇒EF=GF

Chứng minh tương tự ta có GF=GH,GH=EF⇒EF=GF=GH=EH

Do đó tứ giác EFGH là hình thoi.

Bài tập 7

Cho hình thoi ABCD, hai đường chéo AC và BD cắt nhau tại O. Biết AC = 6 cm, BD = 8 cm. Tính độ dài cạnh của hình thoi ABCD.

Gợi ý đáp án

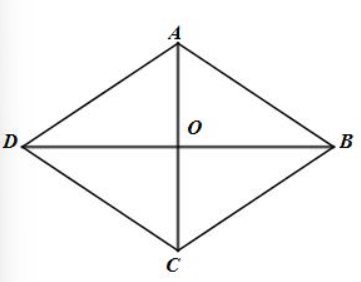
Hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O (gt)

⇒O là trung điểm của AC và BD

⇒AO = \(\frac{AC}{2}$\)và DO = \(\frac{BD}{2}\)

⇒AO = \(\frac{6}{2}\)=3(cm) và DO = \(\frac{8}{2}\) = 4(cm)

AC⊥BD tại O (vì ABCD là hình thoi)

ΔADO vuông tại O có \(AD^{2}=AO^{2}+DO^{2}\) (Định lí Pytago)

⇒\(AD^{2}=3^{2}+4^{2}=25\)⇒AD = 5 (cm)

Vậy AB = BC = DC = AD = 5(cm)

Bài tập 8

Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.

a) Chứng minh tứ giác ABCD là hình thoi.

b) Gọi E, F lần lượt là trung điểm của AB và AC, lấy điểm O sao cho E là trung điểm của OM. Chứng minh hai tam giác AOB và MBO vuông và bằng nhau

b) Chứng minh tứ giác AEMF là hình thoi.

Gợi ý đáp án

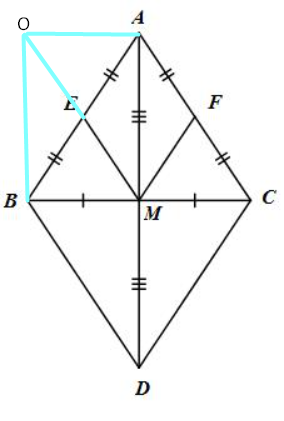
a) Tứ giác ABCD có:

AD và BC cắt nhau tại M (gt);

M là trung điểm của BC (gt)

M là trung điểm của AD (D đối xứng với A qua BC)

Do đó tứ giác ABDC là hình bình hành

Mà AD⊥BC (vì D đối xứng với A qua BC)

Nên hình bình hành ABDC là hình thoi.

b) Tứ giác OAMB có:

OM và AB cắt nhau tại E (gt);

E là trung điểm của OM (gt)

E là trung điểm của AB (gt)

Do đó tứ giác OAMB là hình bình hành

Suy ra \(\widehat{AOB}=\widehat{AMB}=90^{\circ},\widehat{OBM}=\widehat{OAM}=180^{\circ}-90^{\circ}=90^{\circ}\)

Do đó AOB và MBO là tam giác vuông.

Xét tam giác AOB và MBO ta có:

AO = MB (OAMB là hình bình hành)

\(\widehat{AOB}=\widehat{MBO}=90^{\circ}\)

OB chung

Suy ra \(\Delta AOB=\Delta MBO\) (c.g.c)

c) Ta có ME=\(\frac{1}{2}AB\) (đường trung tuyến ứng với cạnh huyền)

Và AE=\(\frac{1}{2}AB\) (E là trung điểm của AB)

⇒EM=EA=\(\frac{1}{2}AB\) (1)

Ta có MF=\(\frac{1}{2}AC\) (đường trung tuyến ứng với cạnh huyền)

Và AF=\(\frac{1}{2}AC\)(F là trung điểm của AC)

⇒MF=AF=\(\frac{1}{2}AC\)(2)

AB=AC(ΔABC cân tại A) (3)

Từ (1), (2) và (3) suy ra EM = EA = MF = AF

Do đó tứ giác AEMF là hình thoi.