Toán 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn Giải SGK Toán 10 trang 30 - Tập 1 sách Kết nối tri thức với cuộc sống

Bài trước

Mục lục

Bài sau

Toán 10 Bài 4 Kết nối tri thức trang 30 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi Luyện tập và 3 bài tập trong SGK bài Hệ bất phương trình bậc nhất hai ẩn.

Giải Toán 10 Kết nối tri thức bài 4 trang 30 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán 10 tập 1. Giải Toán 10 bài 4 Kết nối tri thức là tài liệu cực kì hữu ích hỗ trợ các em học sinh lớp 10 trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.

Giải Toán 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn

Luyện tập Toán 10 Bài 4 Kết nối tri thức

Luyện tập 1

Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hòa hai chiều, một chiều mà cửa hàng cần nhập. Từ HĐ1, viết hệ bất phương trình hai ẩn x, y và chỉ ra một nghiệm của hệ này.

Gợi ý đáp án

Từ HĐ1 ta có hệ bất phương trình:

Ta có x = 30 > 0, y = 50 > 0 thỏa mãn

30 + 50 = 80 ≤ 100

20.30 + 10.50 = 1 100 ≤ 1 200

Do đó x = 30, y = 50 là một nghiệm của hệ bất phương trình đã cho.

Luyện tập 2

Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ: $\left\{ {\begin{array}{*{20}{c}} {x \geqslant 0} \\ {y > 0} \\ {x + y \leqslant 100} \\ {2x + y < 120} \end{array}} \right.$ $\left\{ {\begin{array}{*{20}{c}} {x \geqslant 0} \\ {y > 0} \\ {x + y \leqslant 100} \\ {2x + y < 120} \end{array}} \right.$

Gợi ý đáp án

Xác định miền nghiệm D₁ của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1; 0).

Miền nghiệm D₂ của bất phương trình y > 0 là nửa mặt phẳng bờ Ox chứa điểm (0; 1) không kể biên.

Miền nghiệm D₃ của bất phương trình x + y ≤ 100:

- Vẽ đường thẳng d: x + y – 100 = 0.

- Vì 0 + 0 = 0 < 100 nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x + y ≤ 100

=> Miền nghiệm D₃của bất phương trình x + y ≤ 100 là nửa mặt phẳng bờ d chứa gốc tọa độ.

Miền nghiệm D₄ của bất phương trình 2x + y < 120:

- Vẽ đường thẳng d’: 2x + y – 120 = 0.

- Vì 2.0 + 0 = 0 < 120 nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình 2x + y < 120

=> Miền nghiệm D₄của bất phương trình 2x + y < 120 là nửa mặt phẳng bờ d’ chứa gốc tọa độ không kể biên.

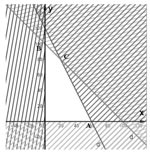
Vậy miền nghiệm của hệ bất phương tình là miền tứ giác OACB với O(0; 0), A(60; 0), C(20; 80), B(0; 100).

Giải Toán 10 Kết nối tri thức Bài 4 trang 30 Tập 1

Bài 2.4 trang 30

Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?

$a) \left\{ \begin{array}{l}x < 0\\y \ge 0\end{array} \right.$ $a) \left\{ \begin{array}{l}x < 0\\y \ge 0\end{array} \right.$

$b) \left\{ \begin{array}{l}x + {y^2} < 0\\y - x > 1\end{array} \right.$ $b) \left\{ \begin{array}{l}x + {y^2} < 0\\y - x > 1\end{array} \right.$

$c) \left\{ \begin{array}{l}x + y + z < 0\\y < 0\end{array} \right.$ $c) \left\{ \begin{array}{l}x + y + z < 0\\y < 0\end{array} \right.$

$d) \left\{ \begin{array}{l} - 2x + y < {3^2}\\{4^2}x + 3y < 1\end{array} \right.$ $d) \left\{ \begin{array}{l} - 2x + y < {3^2}\\{4^2}x + 3y < 1\end{array} \right.$

Gợi ý đáp án

a) Ta thấy hệ $\left\{ \begin{array}{l}x < 0\\y \ge 0\end{array} \right.$ $\left\{ \begin{array}{l}x < 0\\y \ge 0\end{array} \right.$ gồm hai bất phương trình bậc nhất hai ẩn là x < 0 và $y \ge 0$ $y \ge 0$

=> Hệ trên là hệ bất phương trình bậc nhất hai ẩn.

b) Ta thấy hệ $\left\{ \begin{array}{l}x + {y^2} < 0\\y - x > 1\end{array} \right.$ $\left\{ \begin{array}{l}x + {y^2} < 0\\y - x > 1\end{array} \right.$ không là hệ bất phương trình bậc nhất hai ẩn vì $x + {y^2} < 0$ $x + {y^2} < 0$ không là bất phương trình bậc nhất hai ẩn (chứa {y^2})

c) Ta thấy hệ $\left\{ \begin{array}{l}x + y + z < 0\\y < 0\end{array} \right.$ $\left\{ \begin{array}{l}x + y + z < 0\\y < 0\end{array} \right.$ không là hệ bất phương trình bậc nhất hai ẩn vì x + y + z < 0 không là bất phương trình bậc nhất hai ẩn (có 3 ẩn)

d) Ta có:

$\left\{ \begin{array}{l} - 2x + y < {3^2}\\{4^2}x + 3y < 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2x + y < 9\\16x + 3y < 1\end{array} \right.$ $\left\{ \begin{array}{l} - 2x + y < {3^2}\\{4^2}x + 3y < 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2x + y < 9\\16x + 3y < 1\end{array} \right.$

Đây là hệ bất phương trình bậc nhất hai ẩn và gồm hai bất phương trình bậc nhất hai ẩn là - 2x + y < 9 và 16x + 3y < 1

Bài 2.5 trang 30

Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ:

$a) \left\{ \begin{array}{l}y - x < - 1\\x > 0\\y < 0\end{array} \right.$ $a) \left\{ \begin{array}{l}y - x < - 1\\x > 0\\y < 0\end{array} \right.$

$b) \left\{ \begin{array}{l}x \ge 0\\y \ge 0\\2x + y \le 4\end{array} \right.$ $b) \left\{ \begin{array}{l}x \ge 0\\y \ge 0\\2x + y \le 4\end{array} \right.$

$c) \left\{ \begin{array}{l}x \ge 0\\x + y > 5\\x - y > 0\end{array} \right.$ $c) \left\{ \begin{array}{l}x \ge 0\\x + y > 5\\x - y > 0\end{array} \right.$

Gợi ý đáp án

Xác định miền nghiệm của bất phương trình y - x < - 1

+ Vẽ đường thẳng d: - x + y = - 1

+ Vì - 0 + 0 = 0 > - 1 nên tọa độ điểm O(0;0) không thỏa mãn bất phương trình y - x < - 1

Do đó, miền nghiệm của bất phương trình y - x < - 1 là nửa mặt phẳng bờ d không chứa gốc tọa độ O.

Miền nghiệm của bất phương trình x > 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0) không kể trục Oy.

Miền nghiệm của bất phương trình y < 0 là nửa mặt phẳng bờ Ox chứa điểm (0;-1) không kể trục Ox.

Khi đó miền nghiệm của hệ bất phương trình đã cho là miền màu vàng (Không kể đoạn thẳng AB và các trục tọa độ).

Miền nghiệm của bất phương trình $x \ge 0$ $x \ge 0$ là nửa mặt phẳng bờ Oy chứa điểm (1;0) kể cả trục Oy.

Miền nghiệm của bất phương trình $y \ge 0$ $y \ge 0$ là nửa mặt phẳng bờ Ox chứa điểm (0;1) kể cả trục Ox.

Xác định miền nghiệm của bất phương trình $2x + y \le 4$ $2x + y \le 4$

+ Vẽ đường thẳng d: 2x + y = 4

+ Vì 2.0 + 0 = 0 < 4 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình $2x + y \le 4$ $2x + y \le 4$

Do đó, miền nghiệm của bất phương trình $2x + y \le 4$ $2x + y \le 4$ là nửa mặt phẳng bờ d chứa gốc tọa độ O.

Vậy miền nghiệm của hệ bất phương trình đã cho là miền tam giác OAB (kể cả các đoạn thẳng OA, OB,

Miền nghiệm của bất phương trình x \ge 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0) kể cả trục Oy.

Xác định miền nghiệm của bất phương trình x + y > 5

+ Vẽ đường thẳng d: x + y = 5

+ Vì 0 + 0 = 0 < 5 nên tọa độ điểm O(0;0) không thỏa mãn bất phương trình x + y > 5.

Do đó, miền nghiệm của bất phương trình x + y > 5 là nửa mặt phẳng bờ d không chứa gốc tọa độ O.

Xác định miền nghiệm của bất phương trình x - y < 0

+ Vẽ đường thẳng d: x - y = 0

+ Vì 1 - 0 = 1 > 0 nên tọa độ điểm (1;0) không thỏa mãn bất phương trình x - y < 0

Do đó, miền nghiệm của bất phương trình x - y < 0 là nửa mặt phẳng bờ d’ không chứa điểm (1;0).

Vậy miền nghiệm của hệ bất phương trình đã cho là miền màu nâu (không kể d và d’)

Bài 2.6 trang 30

Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất là 1,6 kg thịt bò và 1,1 kg thịt lợn, giá tiền 1 kg thịt bò là 250 nghìn đồng, 1 kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.

LG a

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.

Gợi ý đáp án:

	Thịt bò	Thịt lợn
Protein	800/1kg	600/1kg
Lipit	200/1kg	400/1kg

a) Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.

Số lượng thịt bò và thịt lợn phải là một số không âm nên ta có: $x \ge 0,y \ge 0.$ $x \ge 0,y \ge 0.$

Một gia đình cần ít nhất 900 đơn vị protein trong thức ăn mỗi ngày nên ta có: $800x + 600y \ge 900 \Leftrightarrow 8x + 6y \ge 9$ $800x + 600y \ge 900 \Leftrightarrow 8x + 6y \ge 9$

Một gia đình cần ít nhất 400 đơn vị protein trong thức ăn mỗi ngày nên ta có: $200x + 400y \ge 400 \Leftrightarrow x + 2y \ge 2$ $200x + 400y \ge 400 \Leftrightarrow x + 2y \ge 2$

Vì gia đình này chỉ mua nhiều nhất là 1,6 kg thịt bò và 1,1 kg thịt lợn nên ta có:

$x \le 1,6 và y \le 1,1.$ $x \le 1,6 và y \le 1,1.$

Vậy ta có hệ: $\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.$ $\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.$

Miền nghiệm của hệ là tứ giác ABCD với

A(1,6;0,2) (giao của d’ và đường thẳng x=1,6)

B(1,6;1,1) (giao của đường thẳng x=1,6 và đường thẳng y=1,1)

C(0,3;1,1) (giao của d và đường thẳng y=1,1)

D(0,6;0,7) (giao của d và d’)

b) Vì số tiền mỗi kg thịt bò và thịt lợn lần lượt là 250 nghìn đồng và 160 nghìn đồng nên ta có

$F\left( {x;y} \right) = 250x + 160y$ $F\left( {x;y} \right) = 250x + 160y$(nghìn đồng)

Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình $\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.$ $\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.$

Ta có F(1,6;0,2)=250.1,6+160.0,2=432.

F(1,6;1,1)=250.1,6+160.1,1=576

F(0,3;1,1)=251

F(0,6;0,7)=262

Giá trị nhỏ nhất là F(0,3;1,1)=251.

Vậy để chi phí ít nhất thì cần mua 0,3kg thịt bò và 1,1 thịt lợn.

Đơn vị của F phải là nghìn đồng.

b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy

biểu diễn F theo x và y.

Gợi ý đáp án:

Vì số tiền mỗi kg thịt bò và thịt lợn lần lượt là 250 nghìn đồng và 160 nghìn đồng nên ta có

$F\left( {x;y} \right) = 250x + 160y$ $F\left( {x;y} \right) = 250x + 160y$ (nghìn đồng)

c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.

Gợi ý đáp án:

Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình

$\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.$ $\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.$

Ta có F(1,6;0,2)=250.1,6+160.0,2=432.

F(1,6;1,1)=250.1,6+160.1,1=576

F(0,3;1,1)=251

F(0,6;0,7)=262

Giá trị nhỏ nhất là F(0,3;1,1)=251.

Vậy để chi phí ít nhất thì cần mua 0,3kg thịt bò và 1,1 thịt lợn.

Lý thuyết Hệ bất phương trình bậc nhất hai ẩn

Cách biểu diễn tập nghiệm của bất phương trình bậc nhất hai ẩn

Cũng như bất phương trình bậc nhất một ẩn, các bất phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học.

Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm của bất phương trình (1) được gọi là miền nghiệm của nó.

Từ đó ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình ax + by ≤ c như sau (tương tự cho bất phương trình ax + by ≥ c)

Bước 1. Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng Δ: ax + by = c.

Bước 2. Lấy một điểm M_o(x_o; y_o) không thuộc Δ (ta thường lấy gốc tọa độ )

Bước 3. Tính ax_o + by_o và so sánh ax_o + by_o với c.

Bước 4. Kết luận

Nếu ax_o + by_o < c thì nửa mặt phẳng bờ Δ chứa M0 là miền nghiệm của ax_o + by_o ≤ c

Nếu ax_o + by_o > c thì nửa mặt phẳng bờ Δ không chứa M0 là miền nghiệm của ax_o + by_o ≤ c

Chia sẻ bởi: