| |
Toán 10 Bài tập ôn tập cuối năm - Kết nối tri thức với cuộc sống Giải SGK Toán 10 trang 95 - Tập 2
Bài trước
Giải Toán lớp 10 trang 95, 96, 97 tập 2 Kết nối tri thức với cuộc sống giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi bài tập trong SGK Bài tập ôn tập cuối năm.
Toán 10 Kết nối tri thức trang 95, 96, 97 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 10. Giải Toán lớp 10 Bài tập ôn tập cuối năm trang 95, 96, 97 Kết nối tri thức sẽ là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn. Vậy sau đây là trọn bộ bài giải Toán 10 Bài tập ôn tập cuối năm mời các bạn cùng theo dõi.
Giải Toán 10 trang 95, 96, 97 Kết nối tri thức với cuộc sống - Tập 2
Giải Toán 10 trang 95, 96, 97 Kết nối tri thức
A. TRẮC NGHIỆM
Bài 1 trang 95
Cho hệ bất phương trình bậc nhất hai ẩn ![]() \(\left\{\begin{matrix}x+y>2\\ x-y\leq 1\end{matrix}\right..\) Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?
\(\left\{\begin{matrix}x+y>2\\ x-y\leq 1\end{matrix}\right..\) Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?
A. (1; 1)
B. (2; 0)
C. (3; 2)
D. (3; -2).
Gợi ý đáp án
Đáp án C
Bài 2 trang 95
Cho tam giác ABC. Có bao nhiêu điểm M thỏa mãn ![]() \(|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}|=3?\)
\(|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}|=3?\)
A. Vô số
B. 1
C. 2
D. 3
Gợi ý đáp án
Đáp án A
Bài 3 trang 95
Biết rằng parabol y = x2 +bx + c có đỉnh là I(1; 4). Khi đó giá trị của b + c là
A. 1
B. 2
C. 3
D. 4.
Gợi ý đáp án
Đáp án C
Bài 4 trang 95
Trong mặt phẳng tọa độ Oxy, cho đường thẳng ![]() \(\Delta : x + 2y -5 = 0\). Tìm mệnh đề sai trong các mệnh đề sau:
\(\Delta : x + 2y -5 = 0\). Tìm mệnh đề sai trong các mệnh đề sau:
A. Vecto ![]() \(\overrightarrow{n}=(1;2)\) là một vecto pháp tuyến của
\(\overrightarrow{n}=(1;2)\) là một vecto pháp tuyến của ![]() \(\Delta\)
\(\Delta\)
B. Vecto ![]() \(\overrightarrow{u}=(2; -1)\) là một vecto chỉ phương của
\(\overrightarrow{u}=(2; -1)\) là một vecto chỉ phương của ![]() \(\Delta\)
\(\Delta\)
C. Đường thẳng ![]() \(\Delta\) song song với đường thẳng
\(\Delta\) song song với đường thẳng ![]() \(d: \left\{\begin{matrix}x=1-2t\\ y=1+t\end{matrix}\right..\)
\(d: \left\{\begin{matrix}x=1-2t\\ y=1+t\end{matrix}\right..\)
D. Đường thẳng ![]() \(\Delta\) có hệ số góc k = 2.
\(\Delta\) có hệ số góc k = 2.
Gợi ý đáp án
Đáp án D
Bài 5 trang 95
Trong khai triển nhị thức Newton của (2 + 3x)4, hệ số của x2 là:
A. 9
![]() \(B. C_{4}^{2}\)
\(B. C_{4}^{2}\)
![]() \(C. 9.C_{4}^{2}\)
\(C. 9.C_{4}^{2}\)
![]() \(D. 36.C_{4}^{2}\)
\(D. 36.C_{4}^{2}\)
Gợi ý đáp án
Đáp án D
Bài 6 trang 95
Một tổ gồm 7 nam và 3 nữ. Chọn ngẫu nhiên hai người. Xác suất để trong hai người được chọn có ít nhất một nữ là:
![]() \(A. \frac{7}{15}\)
\(A. \frac{7}{15}\)
![]() \(B. \frac{8}{15}\)
\(B. \frac{8}{15}\)
![]() \(C. \frac{1}{15}\)
\(C. \frac{1}{15}\)
![]() \(D. \frac{2}{15}\)
\(D. \frac{2}{15}\)
Gợi ý đáp án
Đáp án B
B. TỰ LUẬN
Bài 7 trang 95
Cho các mệnh đề:
P: "Tam giác ABC là tam giác vuông tại A";
Q: "Tam giác ABC có các cạnh thỏa mãn AB2 + AC2 = BC2"
a. Hãy phát biểu các mệnh đề ![]() \(P \Rightarrow Q, Q \Rightarrow P, P \Leftrightarrow Q, \overline{P} \Rightarrow \overline{Q}\). Xét tính đúng sai của các mệnh đề này.
\(P \Rightarrow Q, Q \Rightarrow P, P \Leftrightarrow Q, \overline{P} \Rightarrow \overline{Q}\). Xét tính đúng sai của các mệnh đề này.
b. Dùng các khái niệm "điều kiện cần" và "điều kiện đủ" để diễn rả mệnh đề ![]() \(P \Rightarrow Q.\)
\(P \Rightarrow Q.\)
c. Gọi X là tập hợp các tam giác ABC vuông tại A, Y là tập hợp các tam giác ABC có trung tuyến ![]() \(AM=\frac{1}{2}BC\). Nêu mối quan hệ giữa hai tập hợp X và Y.
\(AM=\frac{1}{2}BC\). Nêu mối quan hệ giữa hai tập hợp X và Y.
Gợi ý đáp án
a.
 \(P \Rightarrow Q\): Nếu tam giác ABC là tam giác vuông tại A thì tam giác ABC có các cạnh thỏa mãn AB2 + AC2 = BC2.
\(P \Rightarrow Q\): Nếu tam giác ABC là tam giác vuông tại A thì tam giác ABC có các cạnh thỏa mãn AB2 + AC2 = BC2. \(Q \Rightarrow P\): Nếu tam giác ABC có các cạnh thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC là tam giác vuông tại A.
\(Q \Rightarrow P\): Nếu tam giác ABC có các cạnh thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC là tam giác vuông tại A. \(P \Leftrightarrow Q\): Tam giác ABC là tam giác vuông tại A khi và chỉ khi tam giác ABC có các cạnh thỏa mãn AB2 + AC2 = BC2
\(P \Leftrightarrow Q\): Tam giác ABC là tam giác vuông tại A khi và chỉ khi tam giác ABC có các cạnh thỏa mãn AB2 + AC2 = BC2 \(\overline{P} \Rightarrow \overline{Q}\): Nếu tam giác ABC không là tam giác vuông tại A thì tam giác ABC có các cạnh thỏa mãn AB2 + AC2
\(\overline{P} \Rightarrow \overline{Q}\): Nếu tam giác ABC không là tam giác vuông tại A thì tam giác ABC có các cạnh thỏa mãn AB2 + AC2  \(\neq\) BC2.
\(\neq\) BC2.
b.
- Tam giác ABC là tam giác vuông tại A là điều kiện đủ để tam giác ABC có các cạnh thỏa mãn AB2 + AC2 = BC2
- Tam giác ABC có các cạnh thỏa mãn AB2 + AC2 = BC2 là điều kiện cần để tam giác ABC là tam giác vuông tại A.
c. Vì nếu tam giác ABC có trung tuyến ![]() \(AM=\frac{1}{2}BC\) thì tam giác ABC vuông tại A.
\(AM=\frac{1}{2}BC\) thì tam giác ABC vuông tại A.
Nên tập hợp X = Y.
Bài 8 trang 96
a. Biểu diễn miền nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau:  \(\left\{\begin{matrix}x+y\leq 6\\ 2x-y\leq 2\\ x\geq 0\\ y\geq 0\end{matrix}\right.\)
\(\left\{\begin{matrix}x+y\leq 6\\ 2x-y\leq 2\\ x\geq 0\\ y\geq 0\end{matrix}\right.\)
b. Từ kết quả câu a, tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D.
Gợi ý đáp án
a. Biểu diển miền nghiệm trên hệ trục tọa độ:
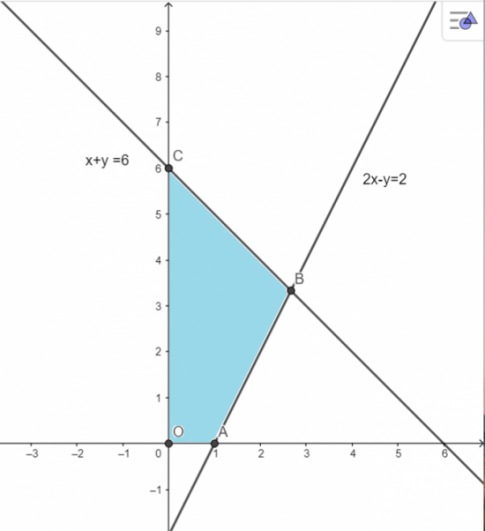
Miền nghiệm của hệ bất phương trình là tứ giác OABC, bao gồm cả các cạnh của tứ giác, với O(0; 0), A(1; 0), ![]() \(B\left ( \frac{8}{3};\frac{10}{3} \right ), C(0; 6).\)
\(B\left ( \frac{8}{3};\frac{10}{3} \right ), C(0; 6).\)
b. Tính giá trị của F lần lươt tại các đỉnh của tứ giác OABC, ta được:
- Giá trị lớn nhất của F trên miền D là: F(0; 6) = 18.
- Giá trị nhỏ nhất của E trên miền D là: F(0; 0) = 0.
Bài 9 trang 96
Cho hàm số y = f(x) = ax2 + bx + c với đồ thị là parabol (P) có đỉnh ![]() \(I\left ( \frac{5}{2};\frac{1}{4} \right )\)và đi qua điểm A(1; 2).
\(I\left ( \frac{5}{2};\frac{1}{4} \right )\)và đi qua điểm A(1; 2).
a. Biết rằng phương trình của parabol có thể viết dưới dạng y = a(x - h)2 + k, trong đó I(h, k) là tọa độ đỉnh của parabol. Hãy xác định phương trình của parabol (P) đã cho và vẽ parabol này.
b. Từ parabol (P) đã vẽ ở câu a, hãy cho biết khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).
c. Giải bất phương trình f(x) \geq 0.
Gợi ý đáp án
a. y = a(x - h)2 + k, mà parabol đi qua điểm ![]() \(I\left ( \frac{5}{2};\frac{1}{4} \right )\) nên ta có:
\(I\left ( \frac{5}{2};\frac{1}{4} \right )\) nên ta có:  \(y = a\left ( x-\frac{5}{2} \right )^{2}+\frac{-1}{4}\)
\(y = a\left ( x-\frac{5}{2} \right )^{2}+\frac{-1}{4}\)
Mà parabol đi qua A(1; 2) nên:  \(2 = a\left ( 1-\frac{5}{2} \right )^{2}+\frac{-1}{4}\)
\(2 = a\left ( 1-\frac{5}{2} \right )^{2}+\frac{-1}{4}\)
![]() \(\Rightarrow a = 1.\)
\(\Rightarrow a = 1.\)
Vậy parabol dạng: y = x2 -5x +6.
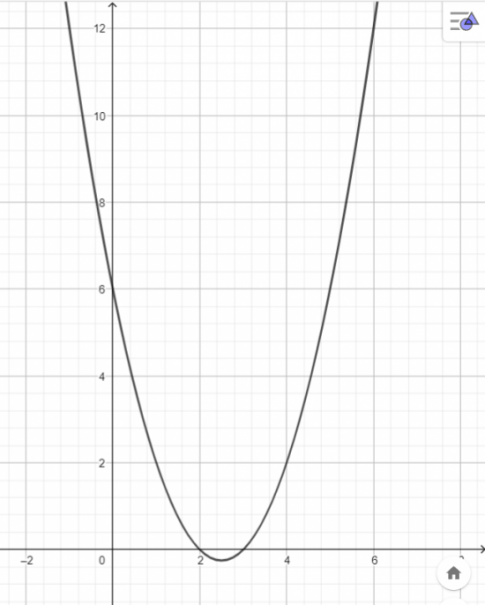
b.
- Hàm số f(x) đồng biến trên khoảng:
 \(\left (\frac{5}{2};+\infty \right)\)
\(\left (\frac{5}{2};+\infty \right)\) - Hàm số f(x) nghịch biến trên khoảng:
 \(\left (-\infty ;\frac{5}{2}; \right).\)
\(\left (-\infty ;\frac{5}{2}; \right).\)
c. f(x) = 0 có hai nghiệm là x1 = 2; x2 = 3, nên![]() \(f(x) \geq 0 \Leftrightarrow x \geq 3\) hoặc
\(f(x) \geq 0 \Leftrightarrow x \geq 3\) hoặc ![]() \(x \leq 2.\)
\(x \leq 2.\)
Bài 10 trang 96
Giải các phương trình chứa căn thức sau:
![]() \(a. \sqrt{2x^{2}-6x+3}=\sqrt{x^{2}-3x+1}\)
\(a. \sqrt{2x^{2}-6x+3}=\sqrt{x^{2}-3x+1}\)
![]() \(b. \sqrt{x^{2}+18x-9}=2x-3\)
\(b. \sqrt{x^{2}+18x-9}=2x-3\)
Gợi ý đáp án
a. Bình phương hai vế của phương trình được:
![]() \(2x^{2}-6x+3 = x^{2}-3x+1\)
\(2x^{2}-6x+3 = x^{2}-3x+1\)
![]() \(\Leftrightarrow x = 2\) hoặc x = 1.
\(\Leftrightarrow x = 2\) hoặc x = 1.
Thử lại giá trị:
- x = 2 không thỏa mãn phương trình.
- x = 1 không thỏa mãn phương trình.
Vậy phương trình vô nghiệm.
b. Bình phương hai vế của phương trình được:
![]() \(x^{2}+18x-9 = 4x^{2} - 12x + 9\)
\(x^{2}+18x-9 = 4x^{2} - 12x + 9\)
![]() \(\Leftrightarrow -3x^{2}+30x-18=0\)
\(\Leftrightarrow -3x^{2}+30x-18=0\)
![]() \(\Leftrightarrow x = 5+\sqrt{19} hoặc x = 5-\sqrt{19}.\)
\(\Leftrightarrow x = 5+\sqrt{19} hoặc x = 5-\sqrt{19}.\)
Thử lại giá trị:
 \(x = 5+\sqrt{19}\) thỏa mãn phương trình.
\(x = 5+\sqrt{19}\) thỏa mãn phương trình. \(x = 5-\sqrt{19}\) không thỏa mãn phương trình.
\(x = 5-\sqrt{19}\) không thỏa mãn phương trình.
Vậy phương trình có nghiệm ![]() \(x = 5+\sqrt{19}.\)
\(x = 5+\sqrt{19}.\)
Bài 11 trang 96
Từ các chữ số 0; 1; 2;.....; 9 có thể lập được tất cả bao nhiêu số tự nhiên nhỏ hơn 1000, chia hết cho 5 và gồm các chữ số khác nhau?
Gợi ý đáp án
Các số tự nhiên lập được nhỏ hơn 1000 và chia hết cho 5 thì: các số đó có thể có 1 chữ số, 2 chữ số, hoặc 3 chữ số và có tận cùng là 0 hoặc 5.
- Số có 1 chữ số, mà chia hết cho 5 là: 0; 5.
- Số có 2 chữ số, gọi số đó có dạng
 \(\overline{ab}, a\neq b, a\neq 0.\)
\(\overline{ab}, a\neq b, a\neq 0.\)
Ta có: b thuộc tập {0; 5}, có 2 cách chọn, chọn a có 9 cách. Nên số cách lập là: 9.2 = 18.
Ta trừ bỏ các số vừa lập được mà có chữ số 0 đứng đầu, số các số đó là: 1.
\Rightarrow Số các số có 2 chữ số lập được thỏa mãn bài toán là: 18 - 1 = 17.
- Số có 3 chữ số, gọi số đó có dạng
 \(\overline{abc}, a\neq b\neq c , a\neq 0.\)
\(\overline{abc}, a\neq b\neq c , a\neq 0.\)
Ta có: chọn c thuộc tập {0; 5}, có 2 cách chọn, chọn a có 9 cách, chọn b có 8 cách. Nên số cách lập là: 2.9.8 = 144.
Ta trừ bỏ các số vừa lập được mà có chữ số 0 đứng đầu, số các số đó là: 8.
![]() \(\Rightarrow\) Số các số có 3 chữ số lập được là: 144 - 8 = 136.
\(\Rightarrow\) Số các số có 3 chữ số lập được là: 144 - 8 = 136.
Vậy số các số lập được là: 2 + 17 + 136 = 155 số.
Bài 12 trang 96
Viết khai triển nhị thức Newton của (2x -1)n, biết n là số tự nhiên thỏa mãn ![]() \(A_{n}^{2}+24C_{n}^{1}=140.\)
\(A_{n}^{2}+24C_{n}^{1}=140.\)
Gợi ý đáp án
- Tìm n, điều kiện
 \(n\geq 2\)
\(n\geq 2\)
 \(A_{n}^{2}+24C_{n}^{1}=140\\\Leftrightarrow \frac{n!}{(n-2)!}+24\frac{n!}{1!.(n-1)!}=140\\\Leftrightarrow n.(n-1)+24.n=140\\\Leftrightarrow n^{2}+23n-140=0\)
\(A_{n}^{2}+24C_{n}^{1}=140\\\Leftrightarrow \frac{n!}{(n-2)!}+24\frac{n!}{1!.(n-1)!}=140\\\Leftrightarrow n.(n-1)+24.n=140\\\Leftrightarrow n^{2}+23n-140=0\)
![]() \(\Leftrightarrow n = 5\) (thỏa mãn) hoặc n = -28 (loại).
\(\Leftrightarrow n = 5\) (thỏa mãn) hoặc n = -28 (loại).
- Với n = 5
(2x -1)5 = (2x)5 + 5(2x)4.(-1) + 10(2x)3.(-1)2 +10(2x)2.(-1)3 + 5(2x)(-1)4 +(-1)5
=32x5 - 80x4 + 80x3 - 40x2 + 10x -1.
Bài 13 trang 96
Từ các công thức tính diện tích tam giác đã được học, hãy chứng minh rằng, trong tam giác ABC, ta có:
 \(r=\frac{\sqrt{(b+c-a)(c+a-b)(a+b-c)}}{2\sqrt{a+b+c}}\)
\(r=\frac{\sqrt{(b+c-a)(c+a-b)(a+b-c)}}{2\sqrt{a+b+c}}\)
Gợi ý đáp án
Gọi ![]() \(p=\frac{a+b+c}{2}\) là nửa chu vi của tam giác.
\(p=\frac{a+b+c}{2}\) là nửa chu vi của tam giác.
Theo công thức có: SABC = p.r, nên r = SABC : p.
Theo công thức Heron: ![]() \(S_{ABC}=\sqrt{p.(p-a).(p-b).(p-c)}\)
\(S_{ABC}=\sqrt{p.(p-a).(p-b).(p-c)}\)
Ta có: ![]() \(p - a = \frac{a+b+c}{2} - a = \frac{b+c-a}{2}.\)
\(p - a = \frac{a+b+c}{2} - a = \frac{b+c-a}{2}.\)
Tương tự ![]() \(p - b = \frac{a+b+c}{2} - b = \frac{a+c-b}{2}.\)
\(p - b = \frac{a+b+c}{2} - b = \frac{a+c-b}{2}.\)
![]() \(p - c = \frac{a+b+c}{2} - c = \frac{a+b-c}{2}.\)
\(p - c = \frac{a+b+c}{2} - c = \frac{a+b-c}{2}.\)
Bài 14 trang 96
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, BC.
a. Biểu thị các vecto  \(\overrightarrow{DM}, \overrightarrow{AN}\) theo các vecto
\(\overrightarrow{DM}, \overrightarrow{AN}\) theo các vecto  \(\overrightarrow{AB}, \overrightarrow{AD}\).
\(\overrightarrow{AB}, \overrightarrow{AD}\).
b. Tính  \(\overrightarrow{DM}.\overrightarrow{AN}\) và tìm góc giữa hai đường thẳng DM và AN.
\(\overrightarrow{DM}.\overrightarrow{AN}\) và tìm góc giữa hai đường thẳng DM và AN.
Gợi ý đáp án
a. Ta có:
 \(\overrightarrow{DM}= \overrightarrow{DA}+\overrightarrow{AM}=-\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}\)
\(\overrightarrow{DM}= \overrightarrow{DA}+\overrightarrow{AM}=-\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}\)
 \(\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}=\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}\)
\(\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}=\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}\)
b.
 \(\overrightarrow{DM}.\overrightarrow{AN}\) =
\(\overrightarrow{DM}.\overrightarrow{AN}\) =  \((-\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}).(\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD})\)
\((-\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}).(\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD})\)
=  \(\frac{-1}{2}\overrightarrow{AD}^{2}-\frac{3}{4}\overrightarrow{AD}.\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AB}^{2}\)
\(\frac{-1}{2}\overrightarrow{AD}^{2}-\frac{3}{4}\overrightarrow{AD}.\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AB}^{2}\)
mà AB, AD vuông góc với nhau nên  \(\overrightarrow{AB}.\overrightarrow{AD}=0\)
\(\overrightarrow{AB}.\overrightarrow{AD}=0\)
 \(\Rightarrow\)
\(\Rightarrow\)  \(\overrightarrow{DM}.\overrightarrow{AN}\) =
\(\overrightarrow{DM}.\overrightarrow{AN}\) =  \(\frac{-1}{2}\overrightarrow{AD}^{2}-\frac{3}{4}\overrightarrow{AD}.\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AB}^{2} = \frac{-1}{2}AD^{2}+\frac{1}{2}AB^{2} = 0\)
\(\frac{-1}{2}\overrightarrow{AD}^{2}-\frac{3}{4}\overrightarrow{AD}.\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AB}^{2} = \frac{-1}{2}AD^{2}+\frac{1}{2}AB^{2} = 0\)
- Do
 \(\overrightarrow{DM}.\overrightarrow{AN}\)
\(\overrightarrow{DM}.\overrightarrow{AN}\)
- = 0 nên đường thẳng DM vuông với đường thẳng AN, hay góc giữa đường thẳng DM và AN là 90 độ.
Bài 15 trang 96
Trong mặt phẳng tọa độ, cho tam giác ABC có ba đỉnh A(-1; 3), B(1; 2), C(4; -2).
a. Viết phương trình đường thẳng BC.
b. Tính diện tích tam giác ABC.
c. Viết phương trình đường tròn có tâm A và tiếp xúc với đường thẳng BC.
Gợi ý đáp án
a.  \(\overrightarrow{BC}(3;-4)\)
\(\overrightarrow{BC}(3;-4)\)
 \(\Rightarrow\) Đường thẳng BC có vecto pháp tuyến là:
\(\Rightarrow\) Đường thẳng BC có vecto pháp tuyến là:  \(\overrightarrow{n}(4;3)\)
\(\overrightarrow{n}(4;3)\)
 \(\Rightarrow\) Phương trình đường thẳng BC là:
\(\Rightarrow\) Phương trình đường thẳng BC là:  \(4(x - 1) + 3(y - 2) = 0\), hay
\(4(x - 1) + 3(y - 2) = 0\), hay  \(4x + 3y -10 = 0\).
\(4x + 3y -10 = 0\).
b.
- Tính khoảng cách từ A đến đường thẳng BC:
 \(d_{(A; BC)}=\frac{|4.(-1)+3.3-10|}{\sqrt{3^{2}+4^{2}}}=1\)
\(d_{(A; BC)}=\frac{|4.(-1)+3.3-10|}{\sqrt{3^{2}+4^{2}}}=1\)
- Tính BC =
 \(\sqrt{3^{2}+4^{2}}=5\)
\(\sqrt{3^{2}+4^{2}}=5\)
 \(\Rightarrow\) Diện tích tam giác ABC là: SABC =
\(\Rightarrow\) Diện tích tam giác ABC là: SABC =  \(\frac{1}{2}d_{(A;BC)}.BC=\frac{1}{2}\).
\(\frac{1}{2}d_{(A;BC)}.BC=\frac{1}{2}\).
Liên kết tải về
Toán 10 Bài tập ôn tập cuối năm - Kết nối tri thức với cuộc sống
484,4 KB
Tải về
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
Chủ đề liên quan
Tìm bài trong mục này
Đóng
Chỉ thành viên Download Pro tải được nội dung này!
Download Pro - Tải nhanh, website không quảng cáo!
Tìm hiểu thêm












 Toán 10 Kết nối tri thức
Toán 10 Kết nối tri thức
 Toán 10 Chân trời sáng tạo
Toán 10 Chân trời sáng tạo
 Toán 10 Cánh Diều
Toán 10 Cánh Diều
 Soạn văn 10 Chân trời sáng tạo
Soạn văn 10 Chân trời sáng tạo
 Soạn văn 10 Cánh Diều
Soạn văn 10 Cánh Diều
 Soạn văn 10 Kết nối tri thức
Soạn văn 10 Kết nối tri thức
 Tiếng Anh 10 Global Success
Tiếng Anh 10 Global Success
 Tiếng anh 10 Friends Global
Tiếng anh 10 Friends Global
 Tiếng Anh 10 Explore New Worlds
Tiếng Anh 10 Explore New Worlds









