Toán 10 Bài 15: Hàm số Giải SGK Toán 10 trang 9 - Tập 2 sách Kết nối tri thức với cuộc sống

Bài trước

Mục lục

Bài sau

Giải Toán lớp 10 trang 9 tập 2 Kết nối tri thức với cuộc sống giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi bài tập trong SGK bài 15 Hàm số thuộc chương 6 Hàm số, đồ thị và ứng dụng.

Toán 10 Kết nối tri thức trang 9 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 10. Giải Toán lớp 10 trang 9 sẽ là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn. Vậy sau đây là trọn bộ bài giải Toán 10 bài 15: Hàm số mời các bạn cùng theo dõi.

Giải Toán 10 Bài 15: Hàm số

Trả lời câu hỏi Hoạt động Toán 10 Bài 15

Hoạt động 1

Bảng 6.1 cho biết nồng độ bụi PM 2.5 trong không khí theo thời gian trong ngày 25-3-2021 tại một trạm quan trắc ở Thủ đô Hà Nội:

Thời điểm (giờ)	0	4	8	12	16
Nồng độ bụi PM 2.5 (μg/m³)	74,27	64,58	57,9	69,07	81,78

Bảng 6.1 (Theo moitruongthudo.vn)

a) Hãy cho biết nồng độ bụi PM 2.5 tại mỗi thời điểm 8 giờ, 12 giờ, 16 giờ.

b) Trong Bảng 6.1, mỗi thời điểm tương ứng với bao nhiêu giá trị của nồng độ bụi PM 2.5?

Gợi ý đáp án

a) Quan sát Bảng 6.1 ta thấy:

Nồng độ bụi PM 2.5 tại thời điểm 8 giờ là 57,9 μg/m³.

Nồng độ bụi PM 2.5 tại thời điểm 12 giờ là 60,07 μg/m³.

Nồng độ bụi PM 2.5 tại thời điểm 16 giờ là 81,78 μg/m³.

b) Mỗi thời điểm tương ứng với một giá trị của nồng độ bụi PM 2.5.

Hoạt động 2

Quan sát Hình 6.1.

a) Thời gian theo dõi mực nước ở Trường Sa được thể hiện trong hình từ năm nào đến năm nào?

b) Trong khoảng thời gian đó, năm nào mực nước biển trung bình tại Trường Sa cao nhất, thấp nhất?

Gợi ý đáp án

a) Thời gian theo dõi mực nước ỏ Trường Sa được thể hiện trong Hình 6.1 từ năm 2013 đến năm 2019.

b) Trong khoảng thời gian đó, năm 2015 mực nước biển trung bình tại Trường Sa thấp nhất (khoảng 237 mm, điểm thấp nhất trong hình tương ứng với năm này) và năm 2013, năm 2018 mực nước trung bình tại Trường Sa cao nhất (242 mm, hai điểm cao nhất trong hình tương ứng hai năm).

Hoạt động 3

Tính tiền điện

Mức điện tiêu thụ	Giá bán điện (đồng/kWh)
Bậc 1 (từ 0 đến 50 kWh)	1 678
Bậc 2 (từ trên 50 đến 100 kWh)	1 734
Bậc 3 (từ trên 100 đến 200 kWh)	2 014
Bậc 4 (từ trên 200 đến 300 kWh)	2 536
Bậc 5 (từ trên 300 đến 400 kWh)	2 834
Bậc 6 (từ trên 400 kWh trở lên)	2 927

a) Dựa vào Bảng 6.2 về giá bán lẻ điện sinh hoạt, hãy tính số tiền phải trả ứng với mỗi lượng điện tiêu thụ ở Bảng 6.3:

Lượng điện tiêu thụ (kWh)	50	100	200
Số tiền (nghìn đồng)	?	?	?

b) Gọi x là lượng điện tiêu thụ (đơn vị kWh) và y là số tiền phải trả tương ứng (đơn vị nghìn đồng). Hãy viết công thức mô tả sự phụ thuộc của y vào x khi 0 ≤ x ≤ 50.

Gợi ý đáp án

+ Lượng điện tiêu thụ là 50 kWh thì ứng với mức tiêu thụ ở bậc 1 nên số tiền phải trả cho 50 kWh điện này là:

1 678 . 50 = 83 900 (đồng) = 83,9 (nghìn đồng).

+ Lượng điện tiêu thụ là 100 kWh thì 50 kWh đầu tính giá ở bậc 1 và 50 kWh sau tính giá ở bậc 2 nên số tiền phải trả cho 100 kWh điện này là:

1 678 . 50 + 1 734 . 50 = 170 600 (đồng) = 170,6 (nghìn đồng).

+ Lượng điện tiêu thụ là 200 kWh thì 50 kWh đầu tính giá ở bậc 1, 50 kWh tiếp theo tính giá ở bậc 2 và 100 kWh cuối tính giá ở bậc 3 nên số tiền phải trả cho 200 kWh điện này là:

1 678 . 50 + 1 734 . 50 + 2 014 . 100 = 372 000 (đồng) = 372 (nghìn đồng).

Vậy ta điền vào bảng như sau:

Lượng điện tiêu thụ (kWh)	50	100	200
Số tiền (nghìn đồng)	83,9	170,6	372

b) x là lượng điện tiêu thụ (đơn vị kWh), y là số tiền phải trả (đơn vị nghìn đồng).

Vì 0 ≤ x ≤ 50 nên lượng điện tiêu thụ thuộc mức điện bậc 1 với giá bán là 1 678 đồng/ 1 kWh hay 1,678 nghìn đồng/ 1 kWh.

Do đó số tiền phải trả cho x kWh là: y = 1,678 . x = 1,678x (nghìn đồng).

Vậy công thức mô tả sự phụ thuộc của y vào x khi 0 ≤ x ≤ 50 là: y = 1,678x.

Giải Toán 10 trang 9 Kết nối tri thức với cuộc sống Tập 2

Bài 6.1 trang 9

Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì y là hàm số của x?

a. x + y = 1

b. y = x²

c. y² = x

d. x² - y²= 0.

Gợi ý đáp án

Trường hợp y là hàm số của x là: a, b.

Các trường hợp c, d không phải vì một giá trị của x có thể tương ứng với nhiều giá trị của y.

Ví dụ:

c. x =4 => y = 2 hoặc y = -2.

d. x = 2 => y = 2 hoặc y = -2.

Bài 6.2 trang 9

Hãy cho một ví dụ về hàm số được cho bằng bảng hoặc biểu đồ. Hãy chỉ ra tập xác định và tập giá trị của hàm số đó.

Gợi ý đáp án

x	1	2	3	4	5
y	-1	-2	-3	-4	-5

Tập xác định: D ={1; 2; 3; 4; 5}

Tập giá trị: {-1; -2; -3; -4; -5}

Bài 6.3 trang 9

Tìm tập xác định của các hàm số sau:

$a. y = 2x^{3}+3x+1$ $a. y = 2x^{3}+3x+1$

$b. y= \frac{x-1}{x^{2}-3x+2}$ $b. y= \frac{x-1}{x^{2}-3x+2}$

$c. y=\sqrt{x+1}+\sqrt{1-x}.$ $c. y=\sqrt{x+1}+\sqrt{1-x}.$

Gợi ý đáp án

a. Tập xác định: $D = \mathbb{R}$ $D = \mathbb{R}$

b. Điều kiện: $x^{2}-3x+2\neq 0\Leftrightarrow \left\{\begin{matrix}x\neq 1\\ x\neq 2\end{matrix}\right.$ $x^{2}-3x+2\neq 0\Leftrightarrow \left\{\begin{matrix}x\neq 1\\ x\neq 2\end{matrix}\right.$

Tập xác định: $D = \mathbb{R}\setminus \left \{ 1;2 \right \}$ $D = \mathbb{R}\setminus \left \{ 1;2 \right \}$

c. Điều kiện: $\left\{\begin{matrix}x+1\geq 0\\ 1-x\geq 0\end{matrix}\right.\Leftrightarrow -1\leq x\leq 1$ $\left\{\begin{matrix}x+1\geq 0\\ 1-x\geq 0\end{matrix}\right.\Leftrightarrow -1\leq x\leq 1$

Tập xác định: D = [-1; 1]

Bài 6.4 trang 9

Tìm tập xác định và tập giá trị của mỗi hàm số sau:

a. y = -2x +3

$b. y=\frac{-1}{2}x^{2}$ $b. y=\frac{-1}{2}x^{2}$

Gợi ý đáp án

a. Tập xác định: $D = \mathbb{R}$ $D = \mathbb{R}$

Tập giá trị: $\mathbb{R}$ $\mathbb{R}$

b. Tập xác định: $D = \mathbb{R}$ $D = \mathbb{R}$

Có: $x^{2}\geq 0\Rightarrow \frac{-1}{2}x^{2}\leq 0$ $x^{2}\geq 0\Rightarrow \frac{-1}{2}x^{2}\leq 0$

Tập giá trị của hàm số: $(-\infty ;0]$ $(-\infty ;0]$

Bài 6.5 trang 9

Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng.

a. y = -2x+1

$b. y = \frac{-1}{2}x^{2}$ $b. y = \frac{-1}{2}x^{2}$

Gợi ý đáp án

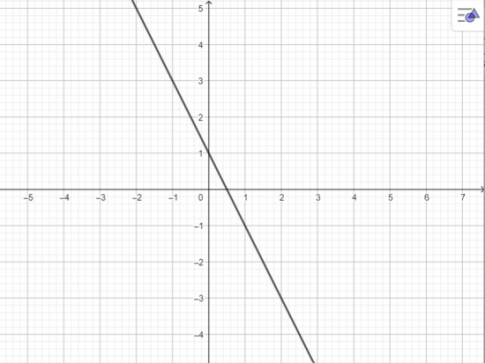
Hàm số nghịch biến trên R

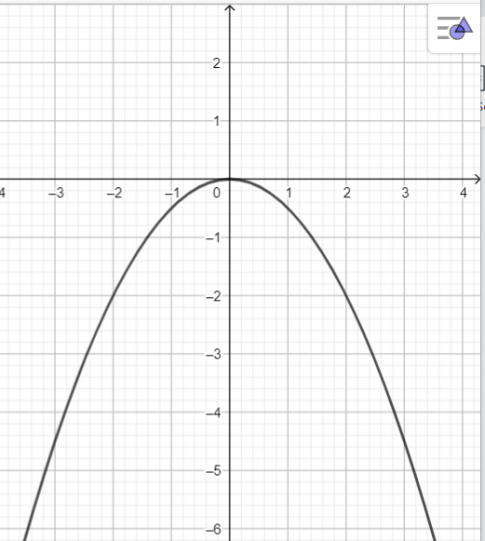
Hàm số nghịch biến trên khoảng $(0;+\infty )$ $(0;+\infty )$ và đồng biến trên khoảng $(-\infty; 0)$ $(-\infty; 0)$

Bài 6.6 trang 9

Giá thuê xe ô tô tự lái là 1,2 triệu đồng một ngày cho hai ngày đầu tiên và 900 nghìn đồng cho mỗi ngày tiếp theo. Tổng số tiền T phải trả là một hàm số của số ngày x mà khách thuê xe.

a. Viết công thức của hàm số T = T(x).

b. Tính T(2), T(3), T(5) và cho biết ý nghĩa của mỗi giá trị này.

Gợi ý đáp án

Nếu 0<x≤ 2 thì T(x) = 1,2.x
Nếu x > 2 thì T(x) = 1,2.2 + 0,9.(x - 2) = 0,6 + 0,9.x

T(2) = 1,2.2 = 2,4
T(3) = 0,6 +0,9.3 = 3,3
T(5) = 0,6 + 0,9.5 = 5,1

Ý nghĩa các giá trị: T(2), T(3), T(5) lần lượt là số tiền phải trả nếu khách thuê 2 ngày, 3 ngày, 5 ngày

Lý thuyết Hàm số

1. Khái niệm hàm số

Nếu với mỗi giá tị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập số thực R thì ta có một hàm số.

Ta gọi x là biến số và y là hàm số của x.

Tập hợp D gọi là tập xác định của hàm số.

Tập tắt cả các giá trị y nhận được, gọi là tập giá trị của hàm số.

2. Đồ thị của hàm số

Đồ thị hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x; f(x)) trên mặt phẳng toạ độ với mọi x thuộc D.

Ví dụ: Viết công thức của hàm số cho ở HĐ3b. Tìm tập xác định, tập giá trị và vẽ đồ thị của hàm số này.

Giải

Công thức của hàm số cho ở HĐ3b là y = 1,678x với $0 \le x \le 50$ $0 \le x \le 50$.

Tập xác định của hàm số này là D = [0: 50]

Vì $0 \le x \le 50 nên 0 \le y \le 1,678.50 = 83,9$ $0 \le x \le 50 nên 0 \le y \le 1,678.50 = 83,9$.

Vậy tập giá trị của hàm số là [0; 83,9].

Đỏ thị của hàm số y = 1,678x trên [0; 50] là một đoạn thẳng.

3. Sự đồng biến, nghịch biến của hàm số

Hàm số y = f(x) được gọi là đồng biến (tăng) trên khoảng (a; b), nếu

$\forall {x_1},{x_2} \in \left( {a,b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)$ $\forall {x_1},{x_2} \in \left( {a,b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)$.

Hàm số y = f(x) được gọi là nghịch biến (giảm) trên khoảng (a; b), nếu

$\forall {x_1},{x_2} \in \left( {a,b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)$ $\forall {x_1},{x_2} \in \left( {a,b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)$.

Chia sẻ bởi: