Toán 10 Bài 25: Nhị thức Newton Giải SGK Toán 10 trang 74 - Tập 2 sách Kết nối tri thức với cuộc sống

Bài trước

Mục lục

Bài sau

Giải Toán lớp 10 trang 74, 75 tập 2 Kết nối tri thức với cuộc sống giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi bài tập trong SGK bài 25 Nhị thức Newton thuộc Chương 8 Đại số tổ hợp.

Toán 10 Kết nối tri thức trang 74, 75 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 10. Giải Toán lớp 10 trang 74, 75 Kết nối tri thức sẽ là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn. Vậy sau đây là trọn bộ bài giải Toán 10 bài 25: Nhị thức Newton mời các bạn cùng theo dõi.

Giải Toán 10 Bài 25: Nhị thức Newton

Trả lời câu hỏi Hoạt động Toán 10 Bài 25

Hoạt động 1

Hãy xây dựng sơ đồ hình cây của tích hai nhị thức (a+b).(c+d) như sau:

Từ một điểm gốc, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức (gọi là nhãn của mũi tên) của nhị thức thứ nhất (H.8.6);
Từ ngọn của mỗi mũi tên đã xây dựng, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức của nhị thức thứ hai;
Tại ngọn của các mũi tên xây dựng tại bước sau cùng, ghi lại tích của các nhã̉n của các mũi tên đi từ điểm gốc đến đầu mút đó.

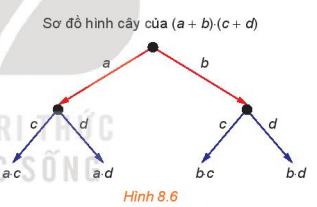
Hãy lấy tổng của các tích nhận được và so sánh kết quả với khai triển của tích (a+b).(c+d)

Hướng dẫn giải:

Tổng các tích nhận được: a.c + a.d + b.c + c.d

Khai triển của tích (a+b).(c+d) = a.c + a.d + b.c + c.d

Vậy tổng của các tích nhận được bằng với khai triển của tích (a+b).(c+d)

Hoạt động 2

Hãy cho biết các đơn thức còn thiếu (...) trong sơ đồ hình cây (H.8.7) của tích (a +b).(a +b).(a +b)

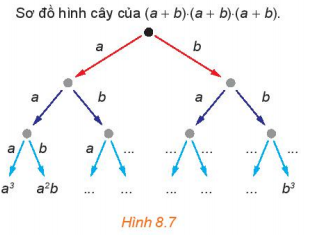
Có bao nhiêu tích nhận được lần lượt bằng a³, a²b, ab², b³?

Hãy so sánh chúng với các hệ số nhận được khi khai triển (a + b)³.

Gợi ý đáp án

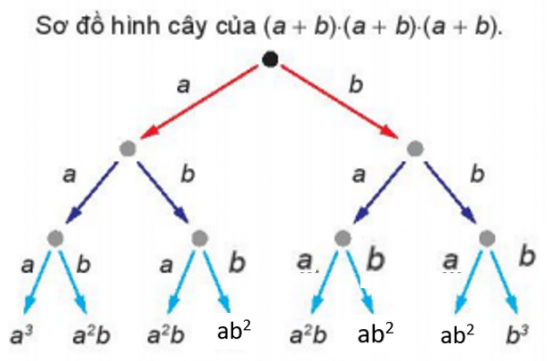
Có 1 tích bằng a³, có 3 tích bằng a²b, có 3 tích bằng ab², có 1 tích bằng b³.
Khai triển (a + b)³ = a³+ a²b + ab²+ b³

⇒ Vậy hệ số của khai triển đúng bằng hệ số các tích nhận được.

Giải Toán 10 trang 74, 75 Kết nối tri thức - Tập 2

Bài 8.12 trang 74

Khai triển các đa thức:

a. (x -3)⁴

b. (3x - 2y)⁴

Gợi ý đáp án

a. (x -3)⁴ = x⁴ + 4.x³.(-3) +6.x².(-3)² +4.x.(-3)³ + (-3)⁴

= x⁴ -12.x³ +54.x² - 108.x +81.

b. (3x - 2y)⁴ = (3x)⁴ + 4.(3x)³(2y) + 6.(3x)².(2y)² + 4.(3x).(2y)³+ (2y)⁴

= 81x⁴ + 216x³y + 216x²y² + 96xy³ + 16y⁴

c. (x+5)⁴ + (x - 5)⁴ = (x⁵+ 5x⁴.5 + 10x³.5² + 10x².5³ +5x.5⁴+ 5⁵) + (x⁵+ 5x⁴.(-5) + 10x³.(-5)² + 10x².(-5)³ + 5x.(-5)⁴+ (-5)⁵)

= 2x⁵ + 500x³ + 6250x

d. (x - 2y)⁵= x⁵ +5x⁴(2y) + 10x³(2y)² + 10x²(2y)³ +5x(2y)⁴ + (2y)⁵

= x⁵ +10x⁴y + 40x³y² + 80x²y³ + 80xy⁴ + 32y⁵.

Bài 8.13 trang 74

Tìm hệ số của x ⁴ trong khai triển của (3x -1) ⁵

Gợi ý đáp án

Số hạng chứa x⁴ là: 5.(3x)⁴(-1) = -405x⁴.

Vậy hệ số của x⁴ trong khai triển là: -405.

Bài 8.14 trang 74

Biểu diễn $(3+\sqrt{2})^{5}-(3-\sqrt{2})^{5}$ $(3+\sqrt{2})^{5}-(3-\sqrt{2})^{5}$ dưới dạng $a+b\sqrt{2}$ $a+b\sqrt{2}$ với a, b là các số nguyên.

Gợi ý đáp án

$(3+\sqrt{2})^{5}=3^{5}+5.3^{4}.\sqrt{2}+10.3^{3}.(\sqrt{2})^{2}+10.3^{2}.(\sqrt{2})^{3}+5.3.$ $(3+\sqrt{2})^{5}=3^{5}+5.3^{4}.\sqrt{2}+10.3^{3}.(\sqrt{2})^{2}+10.3^{2}.(\sqrt{2})^{3}+5.3.$

$(\sqrt{2})^{4}+(\sqrt{2})^{5}\$3-\sqrt{2})^{5}= 3^{5}-5.3^{4}.\sqrt{2}+10.3^{3}.$ \((\sqrt{2})^{4}+(\sqrt{2})^{5}\\(3-\sqrt{2})^{5}= 3^{5}-5.3^{4}.\sqrt{2}+10.3^{3}.$

$(\sqrt{2})^{2}-10.3^{2}.(\sqrt{2})^{3}+5.3.(\sqrt{2})^{4}-(\sqrt{2})^{5}\\$ $(\sqrt{2})^{2}-10.3^{2}.(\sqrt{2})^{3}+5.3.(\sqrt{2})^{4}-(\sqrt{2})^{5}\\$

$\Rightarrow (3+\sqrt{2})^{5}-(3-\sqrt{2})^{5}=810\sqrt{2}+360\sqrt{2}+8\sqrt{2}=1178\sqrt{2}$ $\Rightarrow (3+\sqrt{2})^{5}-(3-\sqrt{2})^{5}=810\sqrt{2}+360\sqrt{2}+8\sqrt{2}=1178\sqrt{2}$

Bài 8.15 trang 75

a. Dùng hai số hạng đầu tiên trong khai triển của (1 + 0,02)⁵ để tính giá trị gần đúng của 1,02⁵

b. Dùng máy tính cầm tay tính giá trị của 1,02⁵và tính sai số tuyệt đối của giá trị gần đúng nhận được ở câu a.

Gợi ý đáp án

a. 1,02⁵=(1 +0,02)⁵ ≈ 1⁵ + 5.1⁴.0,02 = 1,1

b. Ta có: |1,02⁵ - 1,1| < 0,0005

Sai số tuyệt đối là 0,0005.

Bài 8.16 trang 75

Số dân của một tình ở thời điểm hiện tại là khoảng 800 nghìn người. Giả sử rằng tỉ lệ tăng dân số hằng năm của tỉnh đó là r%.

a. Viết công thức tính số dân của tỉnh đó sau 1 năm, sau 2 năm. Từ đó suy ra công thức tính số dân của tỉnh đó sau 5 năm nữa là $P=800\left (1+\frac{r}{100} \right )^{5}$ $P=800\left (1+\frac{r}{100} \right )^{5}$ (nghìn người).

b. Với r = 1,5%, dùng hai số hạng đầu trong khai triển của (1 + 0,015)⁵ hãy ước tính số dân của tỉnh đó sau 5 năm nữa (theo đơn vị nghìn người).

Gợi ý đáp án

a. Số dân của tỉnh đó sau 1 năm là:

$P_{1}=800 + \frac{r}{100}.800 = 800\left ( 1+\frac{r}{100} \right )$ $P_{1}=800 + \frac{r}{100}.800 = 800\left ( 1+\frac{r}{100} \right )$ (nghìn người).

Số dân của tỉnh đó sau 2 năm là:

$P_{2}=P_{1}+ \frac{r}{100}.P_{1} = P_{1}.(1+ \frac{r}{100}) = 800\left ( 1+\frac{r}{100} \right ).(1+ \frac{r}{100}) = 800\left ( 1+\frac{r}{100} \right )^{2}$ $P_{2}=P_{1}+ \frac{r}{100}.P_{1} = P_{1}.(1+ \frac{r}{100}) = 800\left ( 1+\frac{r}{100} \right ).(1+ \frac{r}{100}) = 800\left ( 1+\frac{r}{100} \right )^{2}$(nghìn người).

Suy ra số dân của tỉnh đó sau 5 năm là: $P_{5}= 800\left ( 1+\frac{r}{100} \right )^{5}$ $P_{5}= 800\left ( 1+\frac{r}{100} \right )^{5}$ (nghìn người).

$b. (1 + 0,015)5 \approx 1^{5}+5.1^{4}.0,015=1,075$ $b. (1 + 0,015)5 \approx 1^{5}+5.1^{4}.0,015=1,075$

Số dân của tỉnh đó sau 5 năm xấp xỉ là: 800.1,075 = 860 nghìn người.

Chia sẻ bởi: