Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ Giải SGK Toán 10 trang 65 - Tập 1 sách Kết nối tri thức với cuộc sống
Toán 10 Bài 10 Kết nối tri thức trang 65 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi phần luyện tập và 5 bài tập trong SGK bài Vectơ trong mặt phẳng tọa độ thuộc chương 4 Vectơ.
Giải Toán 10 Kết nối tri thức Bài 10 trang 65 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán 10 tập 1. Giải Toán 10 Bài 10 Kết nối tri thức là tài liệu cực kì hữu ích hỗ trợ các em học sinh lớp 10 trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.
Giải Toán 10 trang 65: Vectơ trong mặt phẳng tọa độ
- Câu hỏi Hoạt động Toán 10 Bài 10
- Trả lời các câu hỏi Luyện tập Toán 10 Bài 10
- Giải Toán 10 trang 65 Kết nối tri thức Tập 1
Câu hỏi Hoạt động Toán 10 Bài 10
Hoạt động 1
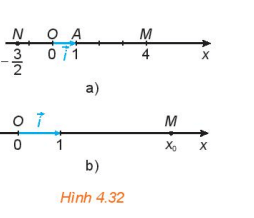
Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt ![]() \(\overrightarrow {OA} = \overrightarrow i\). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số
\(\overrightarrow {OA} = \overrightarrow i\). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số ![]() \(- \frac{3}{2}\). Hãy biểu thị mỗi vecto
\(- \frac{3}{2}\). Hãy biểu thị mỗi vecto ![]() \(\overrightarrow {OM} ;\overrightarrow {ON}\) theo vecto đơn vị
\(\overrightarrow {OM} ;\overrightarrow {ON}\) theo vecto đơn vị ![]() \(\overrightarrow i\)
\(\overrightarrow i\)
Gợi ý đáp án
Ta có:
![]() \(\overrightarrow {OM}\) cùng hướng với
\(\overrightarrow {OM}\) cùng hướng với ![]() \(\overrightarrow {OA}\) và OM = 4OA
\(\overrightarrow {OA}\) và OM = 4OA
=> ![]() \(\overrightarrow {OM} = 4\overrightarrow {OA} = 4\overrightarrow i\)
\(\overrightarrow {OM} = 4\overrightarrow {OA} = 4\overrightarrow i\)
![]() \(\overrightarrow {ON}\)ngược hướng với
\(\overrightarrow {ON}\)ngược hướng với ![]() \(\overrightarrow {OA}\) và ON =
\(\overrightarrow {OA}\) và ON = ![]() \(- \frac{3}{2}\)OA
\(- \frac{3}{2}\)OA
=> ![]() \(\overrightarrow {ON} = - \frac{3}{2}\overrightarrow {OA} = - \frac{3}{2}\overrightarrow i\)
\(\overrightarrow {ON} = - \frac{3}{2}\overrightarrow {OA} = - \frac{3}{2}\overrightarrow i\)
Hoạt động 2
Trong Hình 4.33:
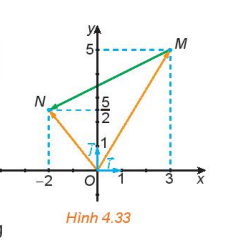
a) Hãy biểu thị mỗi vecto ![]() \(\overrightarrow {OM} ;\overrightarrow {ON}\) theo các vecto
\(\overrightarrow {OM} ;\overrightarrow {ON}\) theo các vecto ![]() \(\overrightarrow i ;\overrightarrow j\)
\(\overrightarrow i ;\overrightarrow j\)
b) Hãy biểu thị vecto ![]() \(\overrightarrow {MN}\) theo các vecto
\(\overrightarrow {MN}\) theo các vecto ![]() \(\overrightarrow {OM} ;\overrightarrow {ON}\) từ đó biểu thị vecto
\(\overrightarrow {OM} ;\overrightarrow {ON}\) từ đó biểu thị vecto ![]() \(\overrightarrow {MN}\) theo các vecto
\(\overrightarrow {MN}\) theo các vecto
Gợi ý đáp án
Kí hiệu như hình vẽ sau:
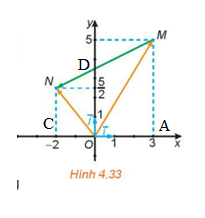
a) Xét hình bình hành OAMB có:
![]() \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} = 3\overrightarrow i + 5\overrightarrow j\)
\(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} = 3\overrightarrow i + 5\overrightarrow j\)
Xét hình bình hành OCND có:
![]() \(\overrightarrow {ON} = \overrightarrow {OC} + \overrightarrow {OD} = - 2\overrightarrow i + \frac{5}{2}\overrightarrow j\)
\(\overrightarrow {ON} = \overrightarrow {OC} + \overrightarrow {OD} = - 2\overrightarrow i + \frac{5}{2}\overrightarrow j\)
b) Xét tam giác MNO ta có:
![]() \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} = - 2\overrightarrow i + \frac{5}{2}\overrightarrow j - \left( {3\overrightarrow i + 5\overrightarrow j } \right) = - 5\overrightarrow i - \frac{5}{2}\overrightarrow j\)
\(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} = - 2\overrightarrow i + \frac{5}{2}\overrightarrow j - \left( {3\overrightarrow i + 5\overrightarrow j } \right) = - 5\overrightarrow i - \frac{5}{2}\overrightarrow j\)
Trả lời các câu hỏi Luyện tập Toán 10 Bài 10
Luyện tập 1
Tìm tọa độ của ![]() \(\overrightarrow 0\)
\(\overrightarrow 0\)
Phương pháp giải
- Với mỗi vecto ![]() \(\overrightarrow u\) trên mặt phẳng Oxy, có duy nhất cặp số (x0; y0) sao cho
\(\overrightarrow u\) trên mặt phẳng Oxy, có duy nhất cặp số (x0; y0) sao cho ![]() \(\overrightarrow u = {x_0}\overrightarrow i + {y_0}\overrightarrow j\)
\(\overrightarrow u = {x_0}\overrightarrow i + {y_0}\overrightarrow j\)
Ta nói vecto ![]() \(\overrightarrow u\) có tọa độ (x0; y0) và viết
\(\overrightarrow u\) có tọa độ (x0; y0) và viết ![]() \(\overrightarrow u = \left( {{x_0};{y_0}} \right)\) hay
\(\overrightarrow u = \left( {{x_0};{y_0}} \right)\) hay ![]() \(\overrightarrow u \left( {{x_0};{y_0}} \right)\). Các cặp số x0; y0 tương ứng gọi là hoành độ của vecto
\(\overrightarrow u \left( {{x_0};{y_0}} \right)\). Các cặp số x0; y0 tương ứng gọi là hoành độ của vecto ![]() \(\overrightarrow u\)
\(\overrightarrow u\)
Gợi ý đáp án
Ta có:
![]() \(\overrightarrow 0 = 0.\overrightarrow i + 0.\overrightarrow j = > \overrightarrow 0 = \left( {0;0} \right)\)
\(\overrightarrow 0 = 0.\overrightarrow i + 0.\overrightarrow j = > \overrightarrow 0 = \left( {0;0} \right)\)
Vậy tọa độ ![]() \(\overrightarrow 0\) là
\(\overrightarrow 0\) là ![]() \(\overrightarrow 0 \left( {0;0} \right)\)
\(\overrightarrow 0 \left( {0;0} \right)\)
Luyện tập 2
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1), B(3; 3).
a) Các điểm O, A, B có thẳng hàng hay không?
b) Tìm điểm M(x; y) để OABM là một hình bình hành.
Gợi ý đáp án
a) Hai vecto ![]() \(\overrightarrow {OA} = \left( {2;1} \right);\overrightarrow {OB} = \left( {3;3} \right)\) không cùng phương
\(\overrightarrow {OA} = \left( {2;1} \right);\overrightarrow {OB} = \left( {3;3} \right)\) không cùng phương
=> Ba điểm O, A, B không cùng nằm trên cùng một đường thẳng. Vậy chúng không thẳng hàng.
b) Ba điểm O, A, B không thẳng hàng
=> Tứ giác OABM là hình bình hành khi và chỉ khi ![]() \(\overrightarrow {OA} = \overrightarrow {MB}\)
\(\overrightarrow {OA} = \overrightarrow {MB}\)
Ta có: ![]() \(\overrightarrow {OA} = \left( {2;1} \right),\overrightarrow {MB} = \left( {3 - x;3 - y} \right)\)
\(\overrightarrow {OA} = \left( {2;1} \right),\overrightarrow {MB} = \left( {3 - x;3 - y} \right)\)
=> ![]() \(\left\{ {\begin{array}{*{20}{c}}
{2 = 3 - x} \\
{1 = 3 - y}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x = 1} \\
{y = 2}
\end{array} \Rightarrow M\left( {1;2} \right)} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}
{2 = 3 - x} \\
{1 = 3 - y}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x = 1} \\
{y = 2}
\end{array} \Rightarrow M\left( {1;2} \right)} \right.\)
Vậy M(1; 2) là điểm cần tìm
Giải Toán 10 trang 65 Kết nối tri thức Tập 1
Bài 4.16 trang 65
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1; 3), N(4; 2)
a) Tính độ dài các đoạn thẳng OM, ON, MN.
b) Chứng minh rằng tam giác OMN vuông cân.
Gợi ý đáp án
a) Ta có: M(1; 3) và N (4; 2)
![]() \(\Rightarrow \overrightarrow {OM} (1;3),\;\,\overrightarrow {ON} (4;2),\;\overrightarrow {MN} = (4 - 1;2 - 3) = (3; - 1)\)
\(\Rightarrow \overrightarrow {OM} (1;3),\;\,\overrightarrow {ON} (4;2),\;\overrightarrow {MN} = (4 - 1;2 - 3) = (3; - 1)\)
![]() \(\Rightarrow OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{1^2} + {3^2}} = \sqrt {10} ,ON = \left| {\overrightarrow {ON} } \right| = \sqrt {{4^2} + {2^2}} = 2\sqrt 5 ,MN\)
\(\Rightarrow OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{1^2} + {3^2}} = \sqrt {10} ,ON = \left| {\overrightarrow {ON} } \right| = \sqrt {{4^2} + {2^2}} = 2\sqrt 5 ,MN\)
![]() \(= \left| {\overrightarrow {MN} } \right| = \sqrt {{3^2} + {{\left( { - 1} \right)}^2}} = \sqrt {10}\)
\(= \left| {\overrightarrow {MN} } \right| = \sqrt {{3^2} + {{\left( { - 1} \right)}^2}} = \sqrt {10}\)
b) Dễ thấy: ![]() \(OM = \sqrt {10} = MN \Rightarrow \Delta\) OMN cân tại M.
\(OM = \sqrt {10} = MN \Rightarrow \Delta\) OMN cân tại M.
Lại có: ![]() \(O{M^2} + M{N^2} = 10 + 10 = 20 = O{N^2}\)
\(O{M^2} + M{N^2} = 10 + 10 = 20 = O{N^2}\)
![]() \(\Rightarrow\)Theo định lí Pythagore đảo, ta có
\(\Rightarrow\)Theo định lí Pythagore đảo, ta có ![]() \(\Delta OMN\) vuông tại M.
\(\Delta OMN\) vuông tại M.
Vậy ![]() \(\Delta OMN\) vuông cân tại M.
\(\Delta OMN\) vuông cân tại M.
Bài 4.17 trang 65
Trong mặt phẳng tọa độ Oxy, cho các vectơ ![]() \(\overrightarrow a = 3.\overrightarrow i - 2.\overrightarrow j ,\overrightarrow b = \left( {4; - 1} \right)\) và các điểm M (-3; 6), N(3; -3).
\(\overrightarrow a = 3.\overrightarrow i - 2.\overrightarrow j ,\overrightarrow b = \left( {4; - 1} \right)\) và các điểm M (-3; 6), N(3; -3).
a) Tìm mối liên hệ giữa các vectơ ![]() \(\overrightarrow {MN}\)và
\(\overrightarrow {MN}\)và ![]() \(2\;\overrightarrow a - \overrightarrow b .\)
\(2\;\overrightarrow a - \overrightarrow b .\)
b) Các điểm O, M, N có thẳng hàng hay không?
c) Tìm điểm P(x; y) để OMNP là một hình bình hành.
Gợi ý đáp án
a) Ta có: ![]() \(\overrightarrow b = \left( {4; - 1} \right) và \overrightarrow a = 3.\overrightarrow i - 2.\overrightarrow j \;\; \Rightarrow \;\overrightarrow a \;\left( {3; - 2} \right)\)
\(\overrightarrow b = \left( {4; - 1} \right) và \overrightarrow a = 3.\overrightarrow i - 2.\overrightarrow j \;\; \Rightarrow \;\overrightarrow a \;\left( {3; - 2} \right)\)
![]() \(\Rightarrow 2\;\overrightarrow a - \overrightarrow b = \left( {2.3 - 4\;;\;2.\left( { - 2} \right) - \left( { - 1} \right)} \right) = \left( {2; - 3} \right)\)
\(\Rightarrow 2\;\overrightarrow a - \overrightarrow b = \left( {2.3 - 4\;;\;2.\left( { - 2} \right) - \left( { - 1} \right)} \right) = \left( {2; - 3} \right)\)
Lại có: M (-3; 6), N(3; -3)
![]() \(\Rightarrow \overrightarrow {MN} = \left( {3 - \left( { - 3} \right); - 3 - 6} \right) = \left( {6; - 9} \right)\)
\(\Rightarrow \overrightarrow {MN} = \left( {3 - \left( { - 3} \right); - 3 - 6} \right) = \left( {6; - 9} \right)\)
Dễ thấy:![]() \(\left( {6; - 9} \right) = 3.\left( {2; - 3} \right) \Rightarrow \overrightarrow {MN} = 3\left( {2\;\overrightarrow a - \overrightarrow b } \right)\)
\(\left( {6; - 9} \right) = 3.\left( {2; - 3} \right) \Rightarrow \overrightarrow {MN} = 3\left( {2\;\overrightarrow a - \overrightarrow b } \right)\)
b) Ta có:![]() \(\overrightarrow {OM} = \left( { - 3;6} \right) ( do M(-3; 6)) và \overrightarrow {ON} = \left( {3; - 3} \right) (do N (3; -3)).\)
\(\overrightarrow {OM} = \left( { - 3;6} \right) ( do M(-3; 6)) và \overrightarrow {ON} = \left( {3; - 3} \right) (do N (3; -3)).\)
Hai vectơ này không cùng phương (vì ![]() \(\frac{{ - 3}}{3} \ne \frac{6}{{ - 3}}\)).
\(\frac{{ - 3}}{3} \ne \frac{6}{{ - 3}}\)).
Do đó các điểm O, M, N không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
c) Các điểm O, M, N không thẳng hàng nên OMNP là một hình hành khi và chỉ khi ![]() \(\overrightarrow {OM} = \overrightarrow {PN} .\)
\(\overrightarrow {OM} = \overrightarrow {PN} .\)
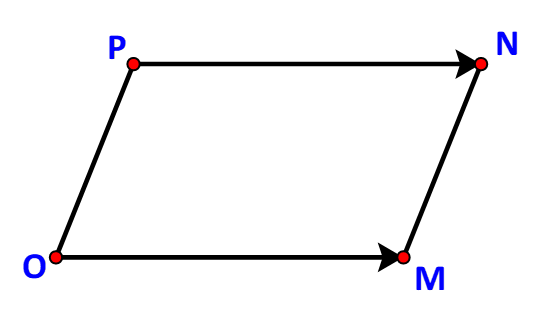
Do ![]() \(\overrightarrow {OM} = \left( { - 3;6} \right),\;\overrightarrow {PN} = \left( {3 - x; - 3 - y} \right)\) nên
\(\overrightarrow {OM} = \left( { - 3;6} \right),\;\overrightarrow {PN} = \left( {3 - x; - 3 - y} \right)\) nên
![]() \(\overrightarrow {OM} = \overrightarrow {PN} \Leftrightarrow \left\{ \begin{array}{l} - 3 = 3 - x\\6 = - 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = - 9\end{array} \right.\)
\(\overrightarrow {OM} = \overrightarrow {PN} \Leftrightarrow \left\{ \begin{array}{l} - 3 = 3 - x\\6 = - 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = - 9\end{array} \right.\)
Vậy điểm cần tìm là P (6; -9).
Bài 4.18 trang 65
Trong mặt phẳng tọa độ Oxy, cho các điểm A(1; 3), B(2; 4), C(-3; 2).
a) Hãy giải thích vì sao các điểm A, B, C không thẳng hàng.
b) Tìm tọa độ trung điểm M của đoạn thẳng AB.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tìm điểm D(x; y) để O(0; 0) là trọng tâm của tam giác ABD.
Gợi ý đáp án
a)
Ta có: ![]() \(\overrightarrow {AB} = \left( {2 - 1;4 - 3} \right) = \left( {1;1} \right),\;\overrightarrow {AC} = \left( { - 3 - 1;2 - 3} \right) = \left( { - 4; - 1} \right)\)
\(\overrightarrow {AB} = \left( {2 - 1;4 - 3} \right) = \left( {1;1} \right),\;\overrightarrow {AC} = \left( { - 3 - 1;2 - 3} \right) = \left( { - 4; - 1} \right)\)
Hai vectơ này không cùng phương (vì ![]() \(\frac{1}{{ - 4}} \ne \frac{1}{{ - 1}}\)).
\(\frac{1}{{ - 4}} \ne \frac{1}{{ - 1}}\)).
Do đó các điểm A, B, C không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
b) Trung điểm M của đoạn thẳng AB có tọa độ là ![]() \(\left( {\frac{{1 + 2}}{2};\frac{{3 + 4}}{2}} \right) = \left( {\frac{3}{2};\frac{7}{2}} \right)\)
\(\left( {\frac{{1 + 2}}{2};\frac{{3 + 4}}{2}} \right) = \left( {\frac{3}{2};\frac{7}{2}} \right)\)
c) Trọng tâm G của tam giác ABC có tọa độ là ![]() \(\left( {\frac{{1 + 2 + \left( { - 3} \right)}}{3};\frac{{3 + 4 + 2}}{3}} \right) = \left( {0;3} \right)\)
\(\left( {\frac{{1 + 2 + \left( { - 3} \right)}}{3};\frac{{3 + 4 + 2}}{3}} \right) = \left( {0;3} \right)\)
d) Để O (0; 0) là trọng tâm của tam giác ABD thì ![]() \(\left( {0;0} \right) = \left( {\frac{{{x_A} + {x_B} + {x_D}}}{3};\frac{{{y_A} + {y_B} + {y_D}}}{3}} \right)\)
\(\left( {0;0} \right) = \left( {\frac{{{x_A} + {x_B} + {x_D}}}{3};\frac{{{y_A} + {y_B} + {y_D}}}{3}} \right)\)
![]() \(\Leftrightarrow \left( {0;0} \right) = \left( {\frac{{1 + 2 + x}}{3};\frac{{3 + 4 + y}}{3}} \right)\)
\(\Leftrightarrow \left( {0;0} \right) = \left( {\frac{{1 + 2 + x}}{3};\frac{{3 + 4 + y}}{3}} \right)\)
 \(\begin{array}{l} \Leftrightarrow \left( {0;0} \right) = \left( {1 + 2 + x;3 + 4 + y} \right)\\ \Leftrightarrow \left( {0;0} \right) = \left( {x + 3;y + 7} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}0 = x + 3\\0 = y + 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = - 7\end{array} \right.\end{array}\)
\(\begin{array}{l} \Leftrightarrow \left( {0;0} \right) = \left( {1 + 2 + x;3 + 4 + y} \right)\\ \Leftrightarrow \left( {0;0} \right) = \left( {x + 3;y + 7} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}0 = x + 3\\0 = y + 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = - 7\end{array} \right.\end{array}\)
Vậy tọa độ điểm D là (-3; -7).
Bài 4.19 trang 65
Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau:
Tàu khởi hành từ vị trí A(1; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vectơ ![]() \(\overrightarrow v = \left( {3;4} \right)\). Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.
\(\overrightarrow v = \left( {3;4} \right)\). Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.
Gợi ý đáp án
Gọi B(x; y) là vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.
Do tàu khởi hành từ A đi chuyển với vận tốc được biểu thị bởi vectơ ![]() \(\overrightarrow v = \left( {3;4} \right)\) nên cứ sau mỗi giờ, tàu đi chuyển được một quãng bằng
\(\overrightarrow v = \left( {3;4} \right)\) nên cứ sau mỗi giờ, tàu đi chuyển được một quãng bằng ![]() \(\left| {\overrightarrow v } \right|.\)
\(\left| {\overrightarrow v } \right|.\)
Vậy sau 1,5 giờ tàu di chuyển tới B, ta được: ![]() \(\overrightarrow {AB} = 1,5.\overrightarrow v\)
\(\overrightarrow {AB} = 1,5.\overrightarrow v\)
 \(\begin{array}{l} \Leftrightarrow (x - 1;y - 2) = 1,5\;.\left( {3;4} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 4,5\\y - 2 = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5,5\\y = 8\end{array} \right.\end{array}\)
\(\begin{array}{l} \Leftrightarrow (x - 1;y - 2) = 1,5\;.\left( {3;4} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 4,5\\y - 2 = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5,5\\y = 8\end{array} \right.\end{array}\)
Vậy sau 1,5 tàu ở vị trí (trên mặt phẳng tọa độ) là B (5,5; 8).
Bài 4.20 trang 65
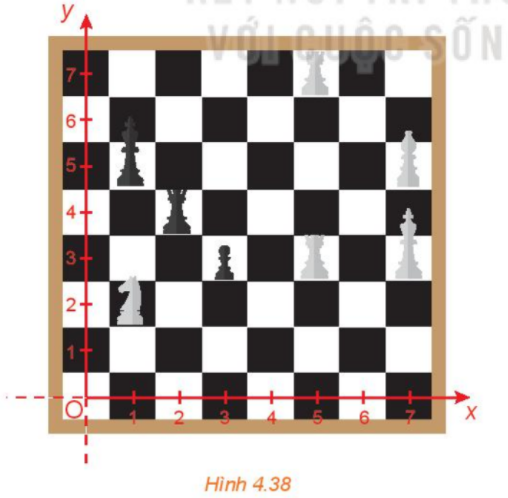
Trong hình 4.38, quân mã đang ở vị trí có tọa độ (1; 2). Hỏi sau một nước đi, quân mã có thể đến những vị trí nào?
Gợi ý đáp án
a) Quân mã đi theo đường chéo hình chữ nhật có chiều dài 3 ô, chiều rộng 2 ô.
Do đó, từ vị trí hiện tại, quân mã có thể đi đến các vị trí A, B, C, D, E, F như dưới đây:
A có tọa độ (3; 3)
B có tọa độ (3; 1)
C có tọa độ (2; 0)
D có tọa độ (0; 0)
E có tọa độ (0; 4)
F có tọa độ (2; 4)
Vậy quân mã có thể đi đến các vị trí A(3;3), B(3;1), C(2;0), D(0;0), E(0;4), F(2;4).
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Toán 10 Kết nối tri thức
Toán 10 Kết nối tri thức
 Toán 10 Chân trời sáng tạo
Toán 10 Chân trời sáng tạo
 Toán 10 Cánh Diều
Toán 10 Cánh Diều
 Soạn văn 10 Chân trời sáng tạo
Soạn văn 10 Chân trời sáng tạo
 Soạn văn 10 Cánh Diều
Soạn văn 10 Cánh Diều
 Soạn văn 10 Kết nối tri thức
Soạn văn 10 Kết nối tri thức
 Tiếng Anh 10 Global Success
Tiếng Anh 10 Global Success
 Tiếng anh 10 Friends Global
Tiếng anh 10 Friends Global
 Tiếng Anh 10 Explore New Worlds
Tiếng Anh 10 Explore New Worlds









