Toán 10 Bài tập cuối chương VI - Kết nối tri thức với cuộc sống Giải SGK Toán 10 trang 28 - Tập 2

Giải Toán lớp 10 trang 28, 29 tập 2 Kết nối tri thức với cuộc sống giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi bài tập trong SGK Bài tập cuối chương VI.

Toán 10 Kết nối tri thức trang 28, 29 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 10. Giải Toán lớp 10 trang 28, 29 Kết nối tri thức tập 2 sẽ là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn. Vậy sau đây là trọn bộ bài giải Toán 10 Bài tập cuối chương VI mời các bạn cùng theo dõi.

Bài tập cuối chương 6 Toán 10 kết nối tri thức

• Giải Toán 10 trang 28, 29 Kết nối tri thức tập 2
• Lý thuyết chương 6 Hàm số đồ thị và ứng dụng

Giải Toán 10 trang 28, 29 Kết nối tri thức tập 2

Bài 6.24 trang 28

Tập xác định của hàm số \(y=\frac{1}{\sqrt{x-2}}\) là:

Gợi ý đáp án

Đáp án B

Bài 6.25 trang 28

Parabol \(y=x^{2}+2x+3\) có đỉnh là:

Gợi ý đáp án

Đáp án D

Bài 6.26 trang 28

Hàm số \(y=x^{2}-5x+4\)

A. Đồng biến trên khoảng \((1; +\infty ).\)

B. Đồng biến trên khoảng \((-\infty; 4 ).\)

C. Nghịch biến trên khoảng \((-\infty; 1 )\)

D. Nghịch biến trên khoảng (1; 4).

Gợi ý đáp án

Đáp án C

Bài 6.27 trang 28

Bất phương trình \(y=x^{2}-2mx+4>0\) nghiệm đúng với mọi \(x\in \mathbb{R}\) khi:

Gợi ý đáp án

Đáp án A

Bài 6.28 trang 28

Tập nghiệm của phương trình \(\sqrt{2x^{2}-3}=x-1\) là:

Gợi ý đáp án

Đáp án C

Bài 6.29 trang 28

Tìm tập xác định của các hàm số sau:

\(a. y = \sqrt{2x-1}+\sqrt{5-x}\)

\(b. y = \frac{1}{\sqrt{x-1}}\)

Gợi ý đáp án

a. Điều kiện: \(\left\{\begin{matrix}2x-1\geq 0\\ 5-x\geq 0\end{matrix}\right.\Leftrightarrow \frac{1}{2}\leq x\leq 5\)

Tập xác định: \(D = \left [ \frac{1}{2};5 \right ]\)

b. Điều kiện: x - 1 > 0

Tập xác định: \(D = (1;+\infty )\)

Bài 6.30 trang 28

Với mỗi hàm số dưới đây, hãy vẽ đồ thị, tìm tập giá trị , khoảng biến thiên, khoảng đồng biến, khoảng nghịch biến của nó:

Gợi ý đáp án

a. Đồ thị hàm số có điểm đỉnh (3; 0)

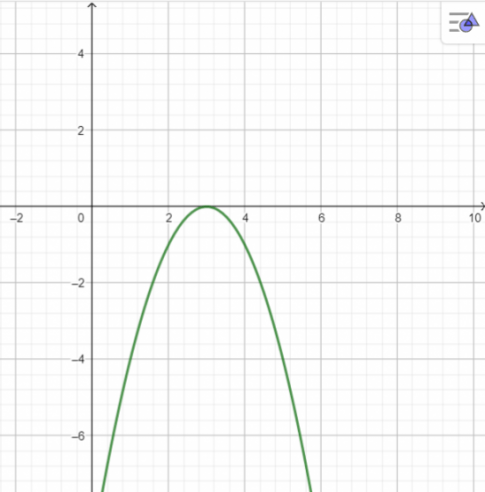
• Tập giá trị: \((-\infty ;0]\)
• Khoảng đồng biến:\((-\infty ;0)\)
• Khoảng nghịch biến: \((0; +\infty )\)

b. Đồ thị hàm số có điểm đỉnh (-2; 5)

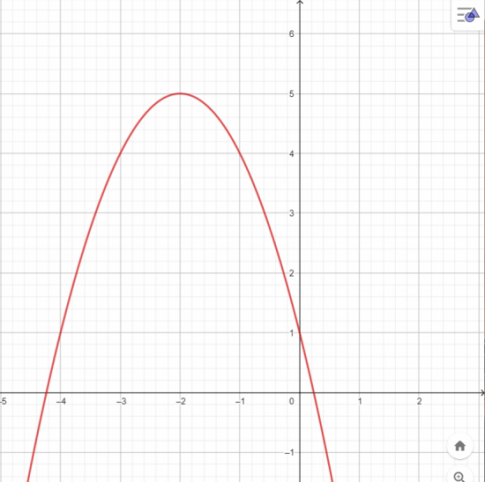
• Tập giá trị: \((-\infty ;5]\)
• Khoảng đồng biến: \((-\infty ;-2)\)
• Khoảng nghịch biến: \((-2; +\infty )\)

c. Đồ thị hàm số có điểm đỉnh (-2; -4)

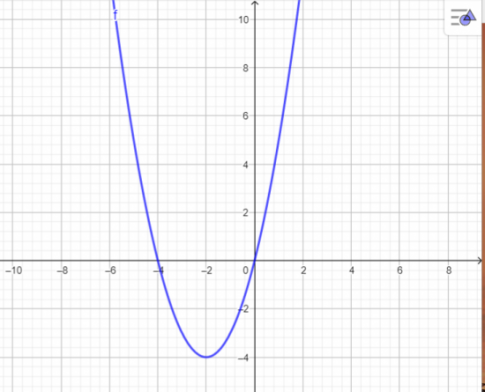
• Tập giá trị: \([-4; +\infty )\)
• Khoảng đồng biến: \((-2; +\infty )\)
• Khoảng nghịch biến: \((-\infty ;-2)\)

d. Đồ thị hàm số có điểm đỉnh \(\left ( \frac{-1}{2}; \frac{1}{2}\right )\)

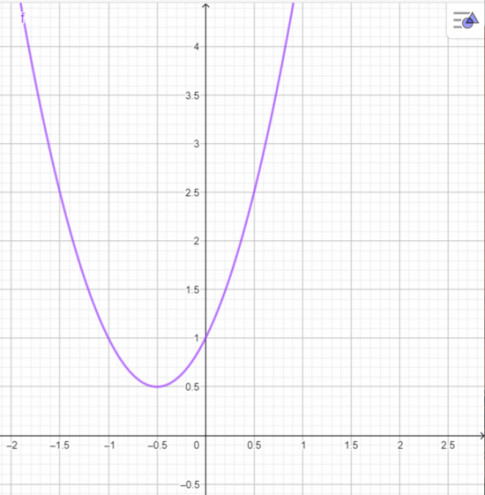
• Tập giá trị: \(\left [ \frac{1}{2};+\infty \right )\)
• Khoảng đồng biến: \(\left ( \frac{-1}{2};+\infty \right )\)
• Khoảng nghịch biến:\(\left ( -\infty; \frac{-1}{2}\right )\)

Bài 6.31 trang 28

Xác định parabol (P): \(y=ax^{2}+bx+3\) trong mỗi trường hợp sau:

a. (P) đi qua hai điểm A(1; 1) và B(-1; 0)

b. (P) đi qua hai điểm M(1; 2) và nhận đường thẳng x =1 làm trục đối xứng.

c. (P) có đỉnh là I(1; 4)

Gợi ý đáp án

a. Thay tọa độ điểm A và B vào hàm số ta có hệ:

\(\left\{\begin{matrix}1=a.1+b.1+3\\ 0=a.1-b+3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=\frac{-5}{2}\\ b=\frac{1}{2}\end{matrix}\right.\)

b. Đồ thị có x = 1 làm trục đối xứng, nên \(\frac{-b}{2a}=1\)

Đồ thị qua M, thay tọa độ điểm M vào hàm số có: 2 = a + b +3.

Ta có hệ:

\(\left\{\begin{matrix}2a+b=0\\ a+b=-1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=1\\ b=-2\end{matrix}\right.\)

c. (P) có đỉnh I(1; 4), nên \(\frac{-b}{2a}=1\)

Đồ thị qua I, thay tọa độ điểm I vào hàm số có: 4 = a + b +3.

Ta có hệ:

\(\left\{\begin{matrix}2a+b=0\\ a+b=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=-1\\ b=2\end{matrix}\right.\)

Bài 6.32 trang 28

Giải các bất phương trình sau:

Gợi ý đáp án

a. Xét tam thức \(y = 2x^{2}-3x+1> có \Delta >0; a=2>0\), có hai nghiệm phân biệt là x = 1 và \(x = \frac{1}{2}\)

\(2x^{2}-3x+1>0\)

\(\Leftrightarrow x\in (-\infty ;\frac{1}{2})\cup (1;+\infty )\)

Vậy tập nghiệm bất phương trình là: \(S = (-\infty ;\frac{1}{2})\cup (1;+\infty )\)

b. Xét tam thức \(y = x^{2}+5x+4 có \Delta >0; a=1>0,\) có hai nghiệm phân biệt là x = -1 và x = -4.

\(x^{2}+5x+4<0\)

\(\Leftrightarrow x\in (-4; -1)\)

Vậy tập nghiệm bất phương trình là: S = (-4; -1)

c. Xét tam thức \(y = -3x^{2}+12x-12\) có \(\Delta =0\); a= -3>0, có nghiệm kép là x = 2.

Suy ra \(4-3x^{2}+12x-12< 0\) với mọi \(x \neq 2.\)

\(-3x^{2}+12x-12\geq 0\)

\(\Leftrightarrow x =2.\)

Vậy tập nghiệm bất phương trình là S = {2}

d. Xét tam thức \(y = 2x^{2}+2x+1\) có \(\Delta <0; a= 2>0\), nên \(2x^{2}+2x+1 > 0\) với mọi \(x \in \mathbb{R}\)

Suy ra bất phương trình \(2x^{2}+2x+1<0\) vô nghiệm.

Vậy bất phương trình vô nghiệm.

Bài 6.33 trang 29

\(a. \sqrt{2x^{2}-14}=x-1\)

\(b. \sqrt{-x^{2}-5x+2}=\sqrt{x^{2}-2x-3}\)

Gợi ý đáp án

a. Bình phương hai vế của phương trình được:

\(2x^{2}-14 = x^{2}-2x+1\)

\(\Leftrightarrow x^{2}+2x-15=0\)

\(\Leftrightarrow x = 3\) hoặc x = -5.

Thử lại giá trị:

• x = 3 thỏa mãn phương trình.
• x = -5 không thỏa mãn phương trình.

Vậy phương trình có nghiệm là x = 3.

b. Bình phương hai vế của phương trình được:

\(-x^{2}-5x+2=x^{2}-2x-3\)

\(\Leftrightarrow x = 1\) hoặc \(x = \frac{-5}{2}\)

Thử lại giá trị

• x = 1 không thỏa mãn phương trình.
• \(x = \frac{-5}{2}\) thỏa mãn phương trình.

Vậy phương trình có nghiệm là \(x = \frac{-5}{2}.\)

Bài 6.34 trang 29

Một công ty bắt đầu sản xuất và bán một loại máy tính xách tay từ năm 2018. Số lượng loại máy tính đó bán được trong hai năm liên tiếp 2018 và 2019 lần lượt là 3,2 nghìn và 4 nghìn chiếc. Theo nghiên cứu dự báo thị trường của công ty, trong khoảng 10 năm kể từ năm 2018, số lượng máy tính loại đó bán được mỗi năm có thể được xấp xỉ bởi một hàm bậc hai.

Giả sử t là thời gian (theo đơn vị năm) tính từ năm 2018. Số lượng loại máy tính đó bán được trong năm 2018 và năm 2019 lần lượt được biểu diên bởi các điểm (0; 3,2) và (1; 4). Giả sử điểm (0; 3,2) là đỉnh đồ thị của hàm số bậc hai này.

a. Lập công thức của hàm số mô tả số lượng máy tính xách tay bán được qua từng năm.

b. Tính số lượng máy tính xách tay đó bán được trong năm 2024.

c. Đến năm bao nhiêu thì số lượng máy tính xách tay đó được bán trong năm sẽ vượt mức 52 nghìn chiếc?

Gợi ý đáp án

a. Gọi hàm số bậc hai mô tả số lượng máy tính xách tay bán qua từng năm có dạng: \(y = at^{2}+bt+c,\)

Với y là số lượng máy tính bán ra (đơn vị: nghìn chiếc), t là thời gian (đơn vị năm). Điều kiện\(t \ge 0.\)

• Do đồ thị hàm số có đỉnh là (0; 3,2) => b = 0, c =3,2.
• Đồ thị đi qua điểm (1; 4) => 4 = a.1 + 3,2, hay \(a=\frac{4}{5}\)

Vậy hàm số có dạng \(y = \frac{4}{5}t^{2}+3,2\)

b. Năm 2024 ứng với t = 6

Số lượng máy tính xách tay bán được là \(y = \frac{4}{5}.6^{2}+3,2 = 32\)

Vậy số lượng máy tính bán được trong năm 2024 là 32 nghìn chiếc.

c. Xét phương trình:

\(\frac{4}{5}.t^{2}+3,2 = 52\)

\(\Rightarrow t \approx 7,81\)

Ứng với t = 8 là năm 2026.

Vây đến năm 2026 thì số lượng máy tính bán ra trong năm vượt mức 52 nghìn chiếc.

Lý thuyết chương 6 Hàm số đồ thị và ứng dụng

1. Hàm số. Tập xác định của hàm số

Giả sử có hai đại lượng biếnthiên x và y, trong đó x nhận giá trị thuộc tập số D.

Nếu với mỗi giá trị của x thuộc tập D có một và chỉ một giá trị tương ứng của x thuộc tập số thực R thì ta có một hàm số.

Ta gọi x là biến số và y là hàm số của x.

Tập hợp D được gọi là tập xác định của hàm số.

2. Cách cho hàm số

Một hàm số có thể được cho bằng các cách sau.

Hàm số cho bằng bảng

Hàm số cho bằng biểu đồ

Hàm số cho bằng công thức

Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

3. Đồ thị của hàm số

Đồ thị của hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x,f(x)) trên mặt phẳng tọa độ với x thuộc D.

4. Hàm số bậc hai

Hàm số bậc hai là hàm số cho bởi công thức y = ax² + bx + c, trong đó x là biến số, a, b, c là các hằng số và a ≠ 0.

Tập xác định của hàm số bậc hai là ℝ.

Nhận xét : Hàm số y = ax² (a ≠ 0) đã học ở lớp 9 là một trường hợp đặc biệt của hàm số bậc hai với b = c = 0.

Ví dụ:

a) Hàm số y = 2x² + x – 1 là hàm số bậc hai với a = 2, b = 1, c = –1.

b) Hàm số y = – x² cũng là hàm số bậc hai với a = –1 và b = c = 0.