Toán 10 Bài 16: Hàm số bậc hai Giải SGK Toán 10 trang 16 - Tập 2 sách Kết nối tri thức với cuộc sống
Toán 10 tập 2 trang 16 giúp các em học sinh lớp 10 có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần mở đầu, hoạt động và bài tập trong SGK bài 16 Hàm số bậc hai thuộc chương 6 Hàm số, đồ thị và ứng dụng được thuận tiện hơn.
Toán 10 Kết nối tri thức tập 2 trang 16 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 10 Kết nối tri thức. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 10 tập 2 Kết nối tri thức trang 16 mời các bạn cùng theo dõi.
Toán 10 Bài 16: Hàm số bậc hai
Phần Mở đầu
Bác Việt có một tấm lưới hình chữ nhật dài 20 m. Bác muốn dùng tấm lưới này rào chắn ba mặt áp bên bờ tường của khu vườn nhà mình thành một mảnh đất hình chữ nhật để trồng rau.
Hỏi hai cột góc hàng rào cần phải cắm cách bờ tường bao xa để mảnh đất được rào chắn của bác có diện tích lớn nhất?
Gợi ý đáp án
Sau bài học này, ta giải quyết được bài toán trên như sau:
Gọi x (mét, x > 0) là khoảng cách từ điểm cọc P và Q đến bờ tường.
Tấm lưới dài 20 m và được rào chắn ba mặt áp lên bờ tường như Hình 6.8, do đó ta có:
x + x + PQ = 20.
Suy ra: PQ = 20 – x – x = 20 – 2x (m).
Vì PQ > 0 (độ dài dương) nên 20 – 2x > 0 ⇔ 2x < 20 ⇔ x < 10.
Do đó ta có điều kiện của x là 0 < x < 10.
Mảnh đất được rào chắn có dạng hình chữ nhật với hai kích thước là x (m) và 20 – 2x (m) với 0 < x < 10.
Khi đó diện tích của mảnh đất là S(x) = x . (20 – 2x) = – 2x2 + 20x.
Theo yêu cầu bài toán, ta cần tìm giá trị của x để S(x) có giá trị lớn nhất.
Ta có: S(x) = – 2(x2 – 10x) = – 2(x2 – 2 . 5 . x + 25) + 50 = – 2(x – 5)2 + 50 ≤ 50 với mọi số thực x.
Dấu “=” xảy ra khi x – 5 = 0 ⇔ x = 5 (thỏa mãn điều kiện 0 < x < 10).
Do đó giá trị lớn nhất của S(x) là 50 tại x = 5.
Vậy hai cột góc hàng rào cần phải cắm cách bờ tường 5 m để mảnh đất được rào chắn của bác Việt có diện tích lớn nhất.
Phần Hoạt động
Hoạt động 1 trang 11 Toán 10 tập 2
Xét bài toán rào vườn ở tình huống mở đầu. Gọi x mét (0 < x < 10) là khoảng cách từ điểm cắm cọc đến bờ tường (H.6.8). Hãy tính theo x.
a) Độ dài cạnh PQ của mảnh đất.
b) Diện tích S(x) của mảnh đất được rào chắn.
Gợi ý đáp án
a) Tấm lưới có chiều dài 20 m, khoảng cách từ điểm cắm cọc tới bờ tường là x (m), ta đóng 2 cọc P và Q, mỗi cọc đều cách tường x (m).
Tấm lưới rào chắn 3 mặt áp bên bờ tường như Hình 6.8 nên x + x + PQ = 20.
Do đó độ dài cạnh PQ của mảnh đất là:
20 – x – x = 20 – 2x (m).
b) Mảnh đất được rào chắn là một hình chữ nhật có hai kích thước là x (m) và 20 – 2x (m).
Do đó diện tích S(x) của mảnh đất được rào chắn là:
S(x) = x . (20 – 2x) = – 2x2 + 20x.
Hoạt động 2 trang 11 Toán 10 tập 2
Xét hàm số y = S(x) = – 2x2 + 20x (0 < x < 10).
a) Trên mặt phẳng tọa độ Oxy, biểu diễn tọa độ các điểm trong bảng giá trị của hàm số lập được ở Ví dụ 1. Nối các điểm đã vẽ lại ta được dạng đồ thị hàm số y = – 2x2 + 20x trên khoảng (0; 10) như trong Hình 6.10. Dạng đồ thị của hàm số y = – 2x2 + 20x có giống với đồ thị của hàm só y = – 2x2 hay không?
b) Quan sát dạng đồ thị của hàm số y = – 2x2 + 20x trong Hình 6.10, tìm tọa độ điểm cao nhất của đồ thị.
c) Thực hiện phép biến đổi
y = – 2x2 + 20x = – 2(x2 – 10x) = – 2(x2 – 2 . 5 . x + 25) + 50 = – 2(x – 5)2 + 50.
Hãy cho biết giá trị lớn nhất của diện tích mảnh đất được rào chắn. Từ đó suy ra lời giải của bài toán ở phần mở đầu.
Gợi ý đáp án
a) Ta biểu diễn các điểm có tọa độ (0; 0), (2; 32), (4; 48), (5; 50), (6; 48), (8; 32), (10; 0) lên mặt phẳng tọa độ và nối lại, ta được dạng của đồ thị hàm số y = – 2x2 + 20x trên khoảng (0; 10).
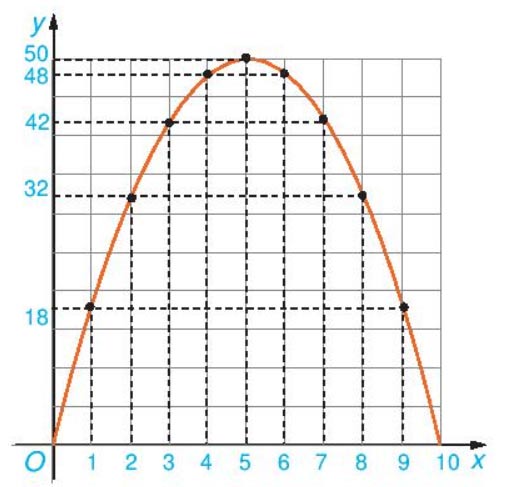
Dạng của đồ thị hàm số y = – 2x2 + 20x giống với dạng của đồ thị hàm số y = – 2x2.
b) Quan sát đồ thị ta thấy tọa độ điểm cao nhất của đồ thị hàm số y = – 2x2 + 20x là điểm (5; 50).
c) Vì (x – 5)2 ≥ 0 với mọi số thực x
Suy ra – 2(x – 5)2 ≤ 0 với mọi số thực x
Do đó: – 2(x – 5)2 + 50 ≤ 0 + 50 = 50 với mọi số thực x.
Khi đó: y ≤ 50. Vậy giá trị lớn nhất của y là 50 hay diện tích lớn nhất của mảnh đất được rào chắn là 50 m2.
Lời giải bài toán mở đầu:
Gọi x (mét, x > 0) là khoảng cách từ điểm cọc P và Q đến bờ tường.
Tấm lưới dài 20 m và được rào chắn ba mặt áp lên bờ tường như Hình 6.8, do đó ta có:
x + x + PQ = 20.
Suy ra: PQ = 20 – x – x = 20 – 2x (m).
Vì PQ > 0 (độ dài dương) nên 20 – 2x > 0 ⇔ 2x < 20 ⇔ x < 10.
Do đó ta có điều kiện của x là 0 < x < 10.
Mảnh đất được rào chắn có dạng hình chữ nhật với hai kích thước là x (m) và 20 – 2x (m) với 0 < x < 10.
Khi đó diện tích của mảnh đất là S(x) = x . (20 – 2x) = – 2x2 + 20x.
Theo yêu cầu bài toán, ta cần tìm giá trị của x để S(x) có giá trị lớn nhất.
Ta có: S(x) = – 2(x2 – 10x) = – 2(x2 – 2 . 5 . x + 25) + 50 = – 2(x – 5)2 + 50 ≤ 50 với mọi số thực x.
Dấu “=” xảy ra khi x – 5 = 0 ⇔ x = 5 (thỏa mãn điều kiện 0 < x < 10).
Do đó giá trị lớn nhất của S(x) là 50 tại x = 5.
Vậy hai cột góc hàng rào cần phải cắm cách bờ tường 5 m để mảnh đất được rào chắn của bác Việt có diện tích lớn nhất.
Hoạt động 3 trang 11 Toán 10 tập 2
Tương tự HĐ2, ta có dạng đồ thị của một số hàm số bậc hai sau.
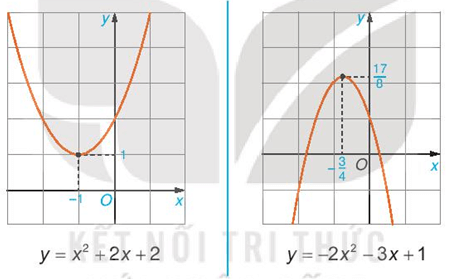
Từ các đồ thị hàm số trên, hãy nêu nội dung thay vào ô có dấu “?” trong bảng sau cho thích hợp.
|
Hàm số |
Hệ số a |
Tính chất của đồ thị |
||
|
Bề lõm của đồ thị (Quay lên/Quay xuống) |
Tọa độ điểm cao nhất/điểm thấp nhất |
Trục đối xứng |
||
|
y = x2 + 2x + 2 |
1 |
Quay lên |
(– 1; 1) |
x = – 1 |
|
y = – 2x2 – 3x + 1 |
? |
? |
? |
? |
Gợi ý đáp án
Quan sát đồ thị hàm số y = – 2x2 – 3x + 1 ta thấy:
+ Hệ số a của hàm số là a = – 2;
+ Bề lõm của đồ thị quay xuống;
+ Đồ thị có điểm cao nhất và điểm này có tọa độ ![]() \(\left(-\frac{3}{4};\frac{17}{8}\right)\)
\(\left(-\frac{3}{4};\frac{17}{8}\right)\)
+ Trục đối xứng ![]() \(x=-\frac{3}{4}\)
\(x=-\frac{3}{4}\)
Vậy ta hoàn thành bảng như sau:
|
Hàm số |
Hệ số a |
Tính chất của đồ thị |
||
|
Bề lõm của đồ thị (Quay lên/Quay xuống) |
Tọa độ điểm cao nhất/điểm thấp nhất |
Trục đối xứng |
||
|
y = x2 + 2x + 2 |
1 |
Quay lên |
(– 1; 1) |
x = – 1 |
|
y = – 2x2 – 3x + 1 |
– 2 |
Quay xuống |
|
|
Phần Bài tập
Bài 6.7 SGK Toán 10 tập 2 trang 16
Vẽ các đường parabol sau:
![]() \(a. y=x^{2}-3x+2\)
\(a. y=x^{2}-3x+2\)
![]() \(b. y=-2x^{2}+2x+3\)
\(b. y=-2x^{2}+2x+3\)
![]() \(c. y=x^{2}+2x+1\)
\(c. y=x^{2}+2x+1\)
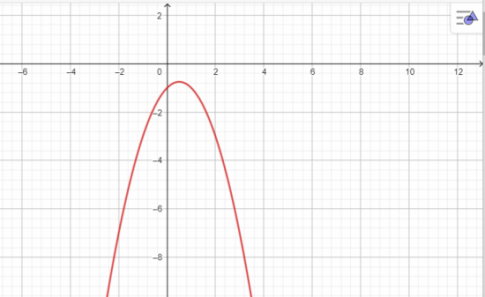
![]() \(d. y=-x^{2}+x-1\)
\(d. y=-x^{2}+x-1\)
Gợi ý đáp án
a.
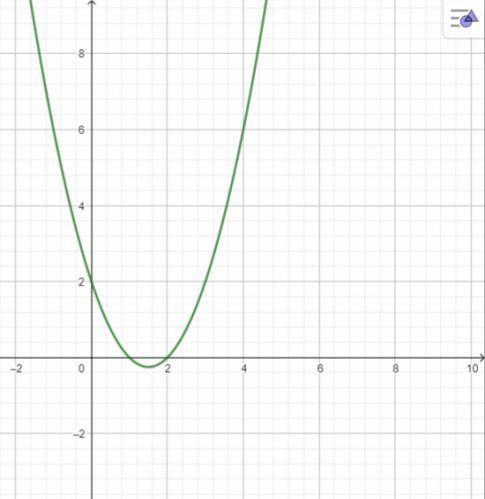
b.
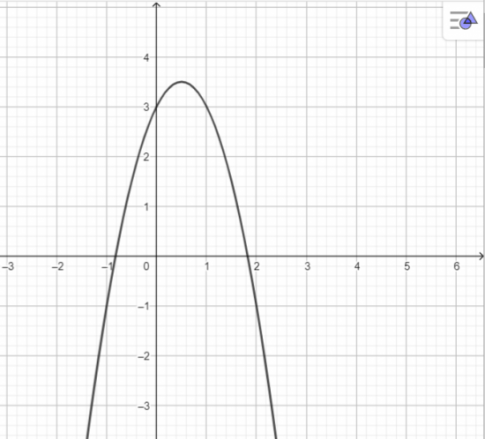
c.
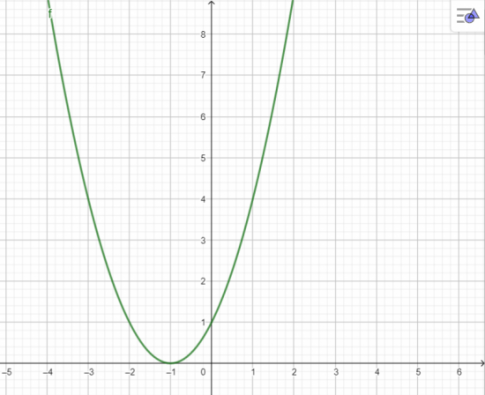
d.
Bài 6.8 SGK Toán 10 tập 2 trang 16
Từ các parabol đã vẽ ở Bài tập 6.7 hãy cho biết khoảng đồng biến và khoảng nghịch biến của mối hàm số bậc hai tương ứng.
Gợi ý đáp án
a. Hàm số đồng biến trên khoảng ![]() \((\frac{3}{2};+\infty )\)
\((\frac{3}{2};+\infty )\)
Hàm số nghịch biến trên khoảng ![]() \((-\infty; \frac{3}{2} ).\)
\((-\infty; \frac{3}{2} ).\)
b. Hàm số đồng biến trên khoảng ![]() \((-\infty; \frac{1}{2}).\)
\((-\infty; \frac{1}{2}).\)
Hàm số nghịch biến trên khoảng ![]() \((\frac{1}{2};+\infty )\)
\((\frac{1}{2};+\infty )\)
c. Hàm số đồng biến trên khoảng ![]() \((-1;+\infty )\)
\((-1;+\infty )\)
Hàm số nghịch biến trên khoảng ![]() \((-\infty; -1 ).\)
\((-\infty; -1 ).\)
d. Hàm số đồng biến trên khoảng ![]() \((-\infty; \frac{1}{2}).\)
\((-\infty; \frac{1}{2}).\)
Hàm số nghịch biến trên khoảng ![]() \((\frac{1}{2};+\infty )\)
\((\frac{1}{2};+\infty )\)
Bài 6.9 SGK Toán 10 tập 2 trang 16
Xác định parabol ![]() \(y = ax^{2}+bx+1\). trong mỗi trường hợp sau:
\(y = ax^{2}+bx+1\). trong mỗi trường hợp sau:
a. Đi qua hai điểm A(1; 0) và B(2; 4)
b. Đi qua điểm A(1; 0) và có trục đối xứng x =1
c. Có đỉnh I(1; 2)
d. Đi qua điểm A(-1; 6) và có tung độ đỉnh -0,25.
Gợi ý đáp án
a. Thay tọa độ điểm A và B vào hàm số ta có hệ phương trình:
 \(\left\{\begin{matrix}0=a.1^{2}+b.1+1\\ 4=a.2^{2}+b.2+1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=\frac{5}{2}\\b=\frac{-7}{2}\end{matrix}\right.\)
\(\left\{\begin{matrix}0=a.1^{2}+b.1+1\\ 4=a.2^{2}+b.2+1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=\frac{5}{2}\\b=\frac{-7}{2}\end{matrix}\right.\)
Vậy parabol ![]() \(y=\frac{5}{2}x^{2}+\frac{-7}{2}x+1\)
\(y=\frac{5}{2}x^{2}+\frac{-7}{2}x+1\)
b. đồ thị có trục đối xứng x = 1
![]() \(=> \frac{-b}{2a}=1\)
\(=> \frac{-b}{2a}=1\)
thay tọa độ của A vào hàm số: ![]() \(0=a.1^{2}+b.1+1\)
\(0=a.1^{2}+b.1+1\)
Ta có hệ phương trình:
![]() \(\left\{\begin{matrix}0=a.1^{2}+b.1+1\\ 0=2.a +b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=1\\ b=-2\end{matrix}\right.\)
\(\left\{\begin{matrix}0=a.1^{2}+b.1+1\\ 0=2.a +b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=1\\ b=-2\end{matrix}\right.\)
c. Có đỉnh I(1; 2) =>![]() \(\frac{-b}{2a}=1\)
\(\frac{-b}{2a}=1\)
Thay tọa độ của I vào hàm số:![]() \(2=a.1^{2}+b.1+1\)
\(2=a.1^{2}+b.1+1\)
Ta có hệ phương trình:
![]() \(\left\{\begin{matrix}2=a.1^{2}+b.1+1\\ 0=2.a +b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=-1\\ b=2\end{matrix}\right.\)
\(\left\{\begin{matrix}2=a.1^{2}+b.1+1\\ 0=2.a +b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=-1\\ b=2\end{matrix}\right.\)
d. Điểm đỉnh của parabol có tọa độ ![]() \(I(\frac{-b}{2a};-0,25)\), thay tọa độ vào hàm số có:
\(I(\frac{-b}{2a};-0,25)\), thay tọa độ vào hàm số có:
 \(-0,25=a.\left ( \frac{-b}{2a} \right )^{2}+b.\left ( \frac{-b}{2a} \right )+1\\\Leftrightarrow -0,25=\frac{b^{2}}{4a}-\frac{b^{2}}{2a}+1\\\Leftrightarrow \frac{b^{2}}{a}=5\\\Leftrightarrow b^{2}=5a\)
\(-0,25=a.\left ( \frac{-b}{2a} \right )^{2}+b.\left ( \frac{-b}{2a} \right )+1\\\Leftrightarrow -0,25=\frac{b^{2}}{4a}-\frac{b^{2}}{2a}+1\\\Leftrightarrow \frac{b^{2}}{a}=5\\\Leftrightarrow b^{2}=5a\)
Thay tọa độ của A vào hàm số: ![]() \(6=a.1^{2}-b.1+1\)
\(6=a.1^{2}-b.1+1\)
Ta có hệ phương trình:
 \(\left\{\begin{matrix}6=a.1^{2}-b.1+1\\ b^{2}=5a\end{matrix}\right.\)
\(\left\{\begin{matrix}6=a.1^{2}-b.1+1\\ b^{2}=5a\end{matrix}\right.\)
Suy ra: ![]() \(b=\frac{5\sqrt{5}+5}{2}, a = \frac{25\sqrt{5}+75}{10}\)
\(b=\frac{5\sqrt{5}+5}{2}, a = \frac{25\sqrt{5}+75}{10}\)
Hoặc ![]() \(b=\frac{-5\sqrt{5}+5}{2}, a = \frac{-25\sqrt{5}+75}{10}\)
\(b=\frac{-5\sqrt{5}+5}{2}, a = \frac{-25\sqrt{5}+75}{10}\)
Bài 6.10 SGK Toán 10 tập 2 trang 16
Xác định parabol ![]() \(y = ax^{2}+bx+1\), biết rằng parabol đó đi qua điểm A(8; 0) và có đỉnh là I(6; -12).
\(y = ax^{2}+bx+1\), biết rằng parabol đó đi qua điểm A(8; 0) và có đỉnh là I(6; -12).
Gợi ý đáp án
Có đỉnh ![]() \(I(6; -12) => \frac{-b}{2a}=6\)
\(I(6; -12) => \frac{-b}{2a}=6\)
Thay tọa độ của I vào hàm số:![]() \(-12=a.6^{2}+b.6+c\)
\(-12=a.6^{2}+b.6+c\)
Thay tọa độ của A vào hàm số: ![]() \(0=a.8^{2}+b.8+c\)
\(0=a.8^{2}+b.8+c\)
Ta có hệ phương trình:
 \(\left\{\begin{matrix}12a+b=0\\ 36a+6b+c=-12\\ 64a+8b+c=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=3\\ b=-36\\ c= 96\end{matrix}\right.\)
\(\left\{\begin{matrix}12a+b=0\\ 36a+6b+c=-12\\ 64a+8b+c=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=3\\ b=-36\\ c= 96\end{matrix}\right.\)
Bài 6.11 SGK Toán 10 tập 2 trang 16
Gọi (P) là đồ thị hàm số bậc hai ![]() \(y = ax^{2}+bx+1\). Hãy xác định dấu của hệ số a và biệt thức
\(y = ax^{2}+bx+1\). Hãy xác định dấu của hệ số a và biệt thức ![]() \(\Delta\), trong mỗi trường hợp sau:
\(\Delta\), trong mỗi trường hợp sau:
a. (P) nằm hoàn toàn phía trên trục hoành.
b. (P) nằm hoàn toàn phía dưới trục hoành.
c. (P) cắt trục hoành tại hai điểm phân biệt và có đỉnh nằm phía dưới trục hoành.
d. (P) tiếp xúc với trục hoành và nằm phía trên trục hoành.
Gợi ý đáp án
a. (P) nằm hoàn toàn phía trên trục hoành thì
- Đồ thị phải quay lên nên a >0.
- Đồ thị không cắt trục hoành nên
 \(\Delta < 0.\)
\(\Delta < 0.\)
b. (P) nằm hoàn toàn phía dưới trục hoành.
- Đồ thị phải quay xuống nên a < 0.
- Đồ thị không cắt trục hoành nên
 \(\Delta < 0.\)
\(\Delta < 0.\)
c. (P) cắt trục hoành tại hai điểm phân biệt và có đỉnh nằm phía dưới trục hoành thì:
- Đồ thị phải quay lên nên a > 0.
- Đồ thị cắt trục hoành tại 2 điểm phân biệt nên
 \(\Delta > 0.\)
\(\Delta > 0.\)
d. (P) tiếp xúc với trục hoành và nằm phía trên trục hoành.
- Đồ thị phải quay lên nên a > 0.
- Đồ thị tiếp xúc với trục hoành nên
 \(\Delta = 0.\)
\(\Delta = 0.\)
Bài 6.12 SGK Toán 10 tập 2 trang 16
Hai bạn An và Bình trao đổi với nhau:
An nói: Tớ đọc ở một tài liệu thấy nói rằng cổng Trường Đại học Bách khoa Hà Nội có dạng một parabol, khoảng cách giữa hai chân cổng là 8m và chiều cao của cổng tính từ một điểm trên mặt đất cách chân cổng là 0,5 m là 2,93 m. Từ đó tớ tính ra được chiều cao của cổng parabol đó là 12m.
Sau một hồi suy nghĩ, Bình nói: Nếu dữ kiện như bạn nói, thì chiều cao của cổng parabol mà bạn tính ra ở trên là không chính xác.
Dựa vào thông tin mà An đọc được, em hãy tính chiều cao của cổng Trường Đại học Bách Khoa Hà Nội để xem kết quả bạn An tính được có chính xác không nhé.
Gợi ý đáp án
Chọn hệ trục tọa độ Oxy sao cho một chân cổng đặt tại gốc tọa độ, chân còn lại đặt trên tia Ox. Khi đó cổng parabol là một phần của đồ thị hàm số dạng ![]() \(y= ax^{2}+bx\) (do parabol đi qua gốc tọa độ nên hệ số tự do bằng 0).
\(y= ax^{2}+bx\) (do parabol đi qua gốc tọa độ nên hệ số tự do bằng 0).
Parabol đi qua các điểm có tọa độ A(8; 0) và B(0,5; 2,93).
Thay tọa độ của A, B vào hàm số ta có:
 \(\left\{\begin{matrix}0=a.8^{2}+b.8\\ 2,93=a.0,5^{2}+b.0,5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=\frac{-293}{375}\\ b=\frac{2344}{375}\end{matrix}\right.\)
\(\left\{\begin{matrix}0=a.8^{2}+b.8\\ 2,93=a.0,5^{2}+b.0,5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=\frac{-293}{375}\\ b=\frac{2344}{375}\end{matrix}\right.\)
Suy ra có hàm số ![]() \(y= \frac{-293}{375}x^{2}+\frac{2344}{375}x\)
\(y= \frac{-293}{375}x^{2}+\frac{2344}{375}x\)
Hàm số có đỉnh ![]() \(I\left ( 4;\frac{4688}{375} \right )\)
\(I\left ( 4;\frac{4688}{375} \right )\)
Suy ra chiều cao của cổng là ![]() \(\frac{4688}{375}\approx 12,5 m.\)
\(\frac{4688}{375}\approx 12,5 m.\)
Kết quả của An gần chính xác.
Bài 6.13 SGK Toán 10 tập 2 trang 16
Bác Hùng dùng 40 m lưới thép gai rào thành một mảnh vườn hình chữ nhật để trồng rau.
a. Tính diện tích mảnh vườn hình chữ nhật rào được theo chiều rộng x (mét) của nó.
b. Tìm kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất mà bác Hùng có thể rào được.
Gợi ý đáp án
a. Chiều dài của mảnh vườn là: 20 - x (m).
Diện tích của mảnh vườn là: ![]() \(x.(20 - x) = 20x-x^{2}.\)
\(x.(20 - x) = 20x-x^{2}.\)
b. Xét đồ thị hàm số ![]() \(y=-x^{2}+20x\) có đỉnh là I(10; 100)
\(y=-x^{2}+20x\) có đỉnh là I(10; 100)
Vây diện tích mảnh vườn lớn nhất là 100 khi kích thước chiều rộng là 10 m, kích thước chiều dài là 10m.
Bài 6.14 SGK Toán 10 tập 2 trang 16
Quỹ đạo của một vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng tọa độ Oxy là một parabol có phương trình ![]() \(y=\frac{-3}{1000}x^{2}+x,\) trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vật so với mặt đất
\(y=\frac{-3}{1000}x^{2}+x,\) trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vật so với mặt đất
a. Tìm độ cao cực đại của vật trong quá trình bay.
b. Tính khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O. Khoảng cách này gọi là tầm xa của quỹ đạo.
Gợi ý đáp án
a. Đồ thị hàm số ![]() \(y=\frac{-3}{1000}x^{2}+x\) có đỉnh là
\(y=\frac{-3}{1000}x^{2}+x\) có đỉnh là ![]() \(I\left ( \frac{500}{3};\frac{250}{3} \right )\)
\(I\left ( \frac{500}{3};\frac{250}{3} \right )\)
Suy ra độ cao cực đại của vật là:![]() \(\frac{250}{3}\approx 83,3 m\)
\(\frac{250}{3}\approx 83,3 m\)
b. Điểm chạm đất sau khi bay của vật có tọa độ A(a; 0) với a là số thực dương.
Ta có: ![]() \(0 = \frac{-3}{1000}x^{2}+x\)
\(0 = \frac{-3}{1000}x^{2}+x\)
![]() \(\Leftrightarrow x_{1}=0; x_{2}=\frac{1000}{3}\)
\(\Leftrightarrow x_{1}=0; x_{2}=\frac{1000}{3}\)
Suy ra: ![]() \(a=\frac{1000}{3}\)
\(a=\frac{1000}{3}\)
Vậy khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O là: ![]() \(\frac{1000}{3}\approx 333,3 m.\)
\(\frac{1000}{3}\approx 333,3 m.\)
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Toán 10 Kết nối tri thức
Toán 10 Kết nối tri thức
 Toán 10 Chân trời sáng tạo
Toán 10 Chân trời sáng tạo
 Toán 10 Cánh Diều
Toán 10 Cánh Diều
 Soạn văn 10 Chân trời sáng tạo
Soạn văn 10 Chân trời sáng tạo
 Soạn văn 10 Cánh Diều
Soạn văn 10 Cánh Diều
 Soạn văn 10 Kết nối tri thức
Soạn văn 10 Kết nối tri thức
 Tiếng Anh 10 Global Success
Tiếng Anh 10 Global Success
 Tiếng anh 10 Friends Global
Tiếng anh 10 Friends Global
 Tiếng Anh 10 Explore New Worlds
Tiếng Anh 10 Explore New Worlds









