Toán 10 Bài 7: Các khái niệm mở đầu Giải SGK Toán 10 trang 50 - Tập 1 sách Kết nối tri thức với cuộc sống

Toán 10 trang 50 Kết nối tri thức - Tập 1 giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi Luyện tập vận dụng và 5 bài tập trong SGK Các khái niệm mở đầu được nhanh chóng và dễ dàng hơn.

Giải Toán 10 Kết nối tri thức trang 50 tập 1 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh lớp 10 học tốt bài 7 Toán 10 Kết nối tri thức. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 10 Kết nối tri thức trang 50 mời các bạn cùng theo dõi.

Toán 10 Bài 7: Các khái niệm mở đầu

• Phần Luyện tập 
• Phần Bài tập 
• Lý thuyết Các khái niệm mở đầu

Phần Luyện tập

Luyện tập 1 trang 49

Cho tam giác ABC với cạnh có độ dài bằng a. Hãy chỉ ra các vecto có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC.

Gợi ý đáp án

Vì tam giác ABC là tam giác đều nên ta có:

AB = AC = BC = a.

=> Các vectơ có độ dài bằng a và có điểm đầu và điểm cuối là các đỉnh của tam giác ABC là:

\(\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {BC} ;\overrightarrow {BA} ;\overrightarrow {CA} ;\overrightarrow {CB}\)

Vậy các vecto thỏa mãn điều kiện đề bài là: \(\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {BC} ;\overrightarrow {BA} ;\overrightarrow {CA} ;\overrightarrow {CB}\)

Luyện tập 2 trang 49

Cho hình thang cân ABCD với hai đáy AB, CD, AB < CD (H.5.10). Hãy chỉ ra mối quan hệ về độ dài, phương, hướng giữa các cặp vecto \(\overrightarrow {AD}\) và \(\overrightarrow {BC}\); \(\overrightarrow {AB}\) và \(\overrightarrow {CD}\); \(\overrightarrow {AC}\) và \(\overrightarrow {BD}\). Có các cặp vecto nào trong các cặp vecto trên bằng nhau hay không?

Gợi ý đáp án

Cặp vecto \(\overrightarrow {AD}\) và \(\overrightarrow {BC}\)

+ Có độ dài bằng nhau (tính chất hình thang cân)

+ Hai vecto không cùng phương với nhau

Cặp vecto \(\overrightarrow {AB}\) và \(\overrightarrow {CD}\)

+ Có độ dài không bằng nhau

+ Có giá song song với nhau nên cùng phương với nhau

+ Hai vecto ngược hướng với nhau

Cặp vecto \(\overrightarrow {AC}\) và \(\overrightarrow {BD}\)

+ Có độ dài bằng nhau (tính chất hình bình hành)

+ Không cùng phương với nhau.

Luyện tập 3 trang 49

Trong các điều kiện dưới đây chọn điều kiện cần và đủ để một điểm M nằm giữa hai điểm phân biệt A và B.

Gợi ý đáp án

Nếu điểm M nằm giữa hai điểm A và B thì \(\overrightarrow {AB} ;\overrightarrow {AM}\) ngược hướng

Nếu \(\overrightarrow {AB} ;\overrightarrow {AM}\) ngược hướng => \(\overrightarrow {AB} ;\overrightarrow {AM}\) cùng phương

=> MA // MB (vô lí) hoặc MA trùng với MB

=> Ba điểm A, B, M thẳng hàng

Mà hai vecto \(\overrightarrow {AB} ;\overrightarrow {AM}\) ngược hướng => Điểm M nằm giữa hai điểm A và B

Điểm M nằm giữa hai điểm A và B khi và chỉ khi \(\overrightarrow {AB} ;\overrightarrow {AM}\) ngược hướng

Vậy điều kiện cần và đủ để một điểm M nằm giữa hai điểm phân biệt A và B là \(\overrightarrow {AB} ;\overrightarrow {AM}\) ngược hướng.

Phần Bài tập

Bài 4.1 trang 50

Cho 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\)đều khác \(\overrightarrow 0\). Những khẳng định nào sau đây là đúng?

a)\(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\) đều cùng hướng với vectơ \(\overrightarrow 0 ;\)

b) Nếu \(\overrightarrow b\)không cùng hướng với \(\overrightarrow a\)thì \(\overrightarrow b\) ngược hướng với \(\overrightarrow a .\)

c) Nếu \(\overrightarrow a\)và \(\overrightarrow b\)đều cùng phương với \(\overrightarrow c\) thì \(\overrightarrow a\)và \(\overrightarrow b\)cùng phương.

d) Nếu \(\overrightarrow a\)và \(\overrightarrow b\)đều cùng hướng với \(\overrightarrow c\)thì \(\overrightarrow a\)và \(\overrightarrow b\)cùng hướng.

Gợi ý đáp án

a) Đúng vì vectơ \(\overrightarrow 0\)cùng hướng với mọi vectơ.

b) Sai. Chẳng hạn: Hai vecto không cùng hướng nhưng cũng không ngược hướng (do chúng không cùng phương).

c) Đúng.

\(\overrightarrow a\)và \(\overrightarrow b\)đều cùng phương với \(\overrightarrow c\)thì a // c và b // c do đó a // b tức là \(\overrightarrow a\)và \(\overrightarrow b\)cùng phương.

d) Đúng.

\(\overrightarrow a\)và \(\overrightarrow b\)đều cùng hướng với \(\overrightarrow c\)thì \(\overrightarrow a\)và \(\overrightarrow b\)cùng phương , cùng chiều đo đó cùng hướng.

Bài 4.2 trang 50

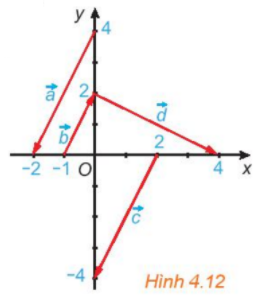
Trong Hình 4.12, hãy chỉ ra các vecto cùng phương, các cặp vecto ngược hướng và các cặp vecto bằng nhau.

Gợi ý đáp án

Các vecto cùng phương là:\(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\)

Trong đó cặp vecto \(\overrightarrow a ,\overrightarrow c\)cùng hướng, cặp \(vecto \overrightarrow a ,\overrightarrow b\) và cặp vecto \(\overrightarrow b ,\overrightarrow c\)ngược hướng.

Bài 4.3 trang 50

Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi \(\overrightarrow {BC} = \overrightarrow {AD}.\)

Gợi ý đáp án

Tứ giác ABCD là một hình bình hành \(\Leftrightarrow \left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\)

\(\Leftrightarrow\)Hai vecto \(\overrightarrow {AD}\) và \(\overrightarrow {BC}\)cùng hướng và AD = BC.

\(\Leftrightarrow \overrightarrow {BC} = \overrightarrow {AD}\) . (đpcm)

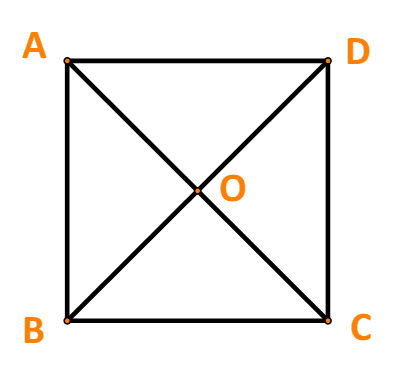
Bài 4.4 trang 50

Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập hợp S gồm tất cả các vecto khác \(\overrightarrow 0\). Hãy chỉ ra tập hợp S gồm tất cả các vceto khác \(\overrightarrow 0 ,\) có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O}. Hãy chia tập S thành các nhóm sao cho hai vecto thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.

Gợi ý đáp án

Tập hợp S là: \(S = \{ \overrightarrow {AB} ;\;\overrightarrow {AC} ;\;\overrightarrow {AD} ;\;\overrightarrow {AO} ;\;\overrightarrow {BA} ;\;\overrightarrow {BC} ;\;\overrightarrow {BD}\) ;\(\;\overrightarrow {BO} ;\;\overrightarrow {CB} ;\;\overrightarrow {CA} ;\;\overrightarrow {CD} ;\;\overrightarrow {CO} ;\;\overrightarrow {DB} ;\;\overrightarrow {DC} ;\;\overrightarrow {DA} ;\;\overrightarrow {DO}\) ;\(\;\overrightarrow {OB} ;\;\overrightarrow {OC} ;\;\overrightarrow {OD} ;\;\overrightarrow {OA} \}\)

Các nhóm trong S là:

\(\begin{array}{l}\{ \overrightarrow {AB} ;\overrightarrow {DC} \} ,\{ \overrightarrow {BA} ;\overrightarrow {CD} \} ,\{ \overrightarrow {AD} ;\overrightarrow {BC} \} ,\{ \overrightarrow {DA} ;\overrightarrow {CB} \} ,\\\{ \overrightarrow {AO} ;\overrightarrow {OC} \} ,\{ \overrightarrow {OA} ;\overrightarrow {CO} \} ,\{ \overrightarrow {OB} ;\overrightarrow {DO} \} ,\{ \overrightarrow {BO} ;\overrightarrow {OD} \} .\end{array}\)

Bài 4.5 trang 50

Trên mặt phẳng tọa độ Oxy hãy vẽ các vecto \(\overrightarrow {OA} ,\;\overrightarrow {MN}\) với A (1; 2), M (0; -1), N (3; 5).

a) Chỉ ra mỗi quan hệ giữa hai vecto trên.

b) Một vật thể khởi hành từ M chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn với vecto \(\overrightarrow v = \overrightarrow {OA} .\) Hỏi vật thể đó có đi qua N hay không? Nếu có thì sau bao lâu sẽ tới N?

Gợi ý đáp án 

Dễ thấy: OA // MN do đó \(\overrightarrow {OA} ,\;\overrightarrow {MN}\) cùng phương.

Hơn nữa, \(\overrightarrow {OA} ,\;\overrightarrow {MN}\) cùng hướng và MN = 3 OA.

b) Mỗi giờ, vật thể đó đi được quãng đường tương ứng với đoạn thẳng OA.

Vì \({MN} = 3. {OA}\) nên vật thể đó sẽ đi qua N sau 3 giờ kể từ lúc khởi hành.

Lý thuyết Các khái niệm mở đầu

Hai Vectơ cùng phương, cùng hướng, bằng nhau

+) Giá của vecto: là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó.

Ví dụ: Giá của vecto \(\overrightarrow {CD}\) là đường thẳng CD

+) Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

+) Hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.

Ví dụ:

Ba vecto \(\overrightarrow u ,\;\overrightarrow {CD} ,\;\overrightarrow {AB}\)cùng phương.

Trong đó 2 vecto \(\overrightarrow u ,\;\overrightarrow {CD}\)cùng hướng, còn 2 vecto \(\overrightarrow {CD} ,\;\overrightarrow {AB}\)ngược hướng.

+) Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.

* Chú ý:

- Chỉ khi hai vecto cùng phương ta mới nói tới chúng cùng hướng hay ngược hướng.

- Vecto \(\overrightarrow 0\)cùng phương, cùng hướng với mọi vecto.

- Với mỗi điểm O và vecto \(\overrightarrow a\)cho trước, có duy nhất điểm A sao cho \(\overrightarrow {OA} = \overrightarrow a\)

* Nhận xét:

+) Ba điểm A, B, C thẳng hàng khi và chỉ khi \(\overrightarrow {AB}\) và \(\overrightarrow {AC}\) cùng phương.

+) Ba điểm A, B, C thẳng hàng, B nằm giữa khi và chỉ khi \(\overrightarrow {AB}\) và \(\overrightarrow {AC}\)cùng hướng.