Toán 10 Bài 22: Ba đường conic Giải SGK Toán 10 trang 56 - Tập 2 sách Kết nối tri thức với cuộc sống

Bài trước

Mục lục

Bài sau

Toán 10 Kết nối tri thức tập 2 trang 56 giúp các em học sinh lớp 10 có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần hoạt động và bài tập trong SGK bài 22 Ba đường conic thuộc chương 7 Phương pháp tọa độ trong mặt phẳng dễ dàng hơn.

Toán 10 tập 2 trang 56 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 10 Kết nối tri thức. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 10 trang 56 tập 2 mời các bạn cùng theo dõi.

Giải Toán 10 Bài 22: Ba đường conic

Phần Hoạt động

Hoạt động 1

Đính hai đầu của một sợi dây không đàn hồi vào hai vị trí cố định F₁, F₂ trên một mặt bàn (độ dài sợi dây lớn hơn khoảng cách giữa hai điểm F₁, F₂). Kéo căng sợi dây tại một điểm M bởi một đầu bút dạ (hoặc phấn). Di chuyển đầu bút dạ để nó vẽ trên mặt bàn một đường khép kín.

a. Đường vừa nhận được có liên hệ với hình ảnh nào ở Hình 7.17?

b. Trong quá trinh đầu bút di chuyển để vẽ nên đường nói trên, tổng các khoảng cách từ nó tới các vị trí F₁, F₂ có thay đổi không? Vì sao?

Gợi ý đáp án

a. Đường nhận được liên hệ với hình b.

b. Tổng các khoảng cách từ đầu bút tới các vị trí F₁, F₂ không thay đổi vì nó luôn bằng độ dài dây

Hoạt động 2

Xét một elip (E) với các kí hiệu như trong định nghĩa. Chọn hệ trục tọa độ Oxy có gốc O là trung điểm của F₁F₂ , tia Ox trùng tia OF₂

a. Nêu tọa độ của các tiêu điểm F₁, F₂

b. Giải thích vì sao điểm M(x; y) thuộc elip khi và chỉ khi: $\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$ $\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$

Gợi ý đáp án

a. Vì F₁F₂ = 2c, mà O là trung điểm của F₁, F₂

Tọa độ của các điểm: F₁(-c; 0) và F2(c; 0)

Giả sử M thuộc elip (E) ta chứng minh:

$\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$ $\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$

. Thật vậy:

M thuộc elip (E) nên: MF₁+ MF₂ = 2a

$\Rightarrow$ $\Rightarrow$ $\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$ $\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$.

Giả sử

$\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$ $\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$

, ta chứng minh M thuộc elip (E). Thật vậy:

$\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$ $\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$ nên: MF₁+ MF₂ = 2a

$\Rightarrow$ $\Rightarrow$ M thuộc elip (E).

Hoạt động 3

Giả sử thiết bị tại F₂ nhận được tín hiệu âm thanh sớm hơn thiết bị tại F₁ là 2 giây và vận tốc âm thanh là 343 m/s.

a) Tìm mối quan hệ giữa các khoảng cách từ nơi phát ra tín hiệu âm thanh tới F₁, F_2.

b) Việc giới hạn khu vực tìm kiếm nơi phát ra tín hiệu âm thanh có liên quan đến bài toán tìm tập hợp những điểm M thỏa mãn MF₁ – MF₂ = 686 (m) hay không?

Lời giải

a) Gọi M là điểm phát tín hiệu âm thanh, t (s) là thời gian âm thanh truyền từ M đến F₂.

Khi đó âm thanh truyền từ M đến F₁ là: t + 2 (s)

Khoảng cách từ M đến F₁ là: MF₁ = 343(t + 2) = 343t + 686 (m).

Khoảng cách từ M đến F₂ là: MF₂ = 343.t = 343t (m).

Suy ra MF₁ – MF₂ = 343t + 686 – 343t = 686 (m).

Vậy hiệu khoảng cách từ nơi phát tín hiệu tới F₁ và tới F₂ luôn không đổi và bằng 686m.

b) Ta thấy nơi phát tín hiệu luôn thỏa mãn hiệu khoảng cách từ nơi phát tín hiệu tới F₁ và tới F₂ luôn không đổi và bằng 686m. Do đó đây chính là bài toán tìm điểm M thỏa mãn MF₁– MF₂ = 686 (m).

Phần Bài tập

Bài 7.19 trang 56

Cho elip có phương trình: $\frac{x^{2}}{36}+\frac{y^{2}}{9}=1$ $\frac{x^{2}}{36}+\frac{y^{2}}{9}=1$. Tìm tiêu điểm và tiêu cự của elip.

Gợi ý đáp án

Ta có: $a2 = 36, b2 = 9, c = \sqrt{a^{2}-b^{2}}=\sqrt{27}.$ $a2 = 36, b2 = 9, c = \sqrt{a^{2}-b^{2}}=\sqrt{27}.$

Tiêu điểm $F1(-\sqrt{27};0) và F2(\sqrt{27};0).$ $F1(-\sqrt{27};0) và F2(\sqrt{27};0).$

Tiêu cự $2c = 2\sqrt{27}.$ $2c = 2\sqrt{27}.$

Bài 7.20 trang 56

Cho hypebol có phương trình: $\frac{x^{2}}{7}-\frac{y^{2}}{9}=1$ $\frac{x^{2}}{7}-\frac{y^{2}}{9}=1$. Tìm tiêu điểm và tiêu cự của hypebol.

Gợi ý đáp án

Ta có: a2 = 7, b2 = 9, $c = \sqrt{a^{2}+b^{2}}=4.$ $c = \sqrt{a^{2}+b^{2}}=4.$

Tiêu điểm F1(-4;0) và F2(4;0).

Tiêu cự 2c = 8

Bài 7.21 trang 56

Cho parabol có phương trình: y² = 8x. Tìm tiêu điểm và đường chuẩn của parabol.

Gợi ý đáp án

Ta có: 2p = 8 nên p = 4.

Tiêu điểm F(2; 0) và đường chuẩn $\Delta : x = -2.$ $\Delta : x = -2.$

Bài 7.22 trang 56

Lập phương trình chính tắc của elip đi qua điểm A(5; 0) và có một tiêu điểm là F2(3; 0).

Gợi ý đáp án

Elip (E) có dạng: $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ với a>b>0.

(E) đi qua A(5; 0) nên $\frac{5^{2}}{a^{2}}+\frac{0^{2}}{b^{2}}=1$ $\frac{5^{2}}{a^{2}}+\frac{0^{2}}{b^{2}}=1$

$\Rightarrow a = 5.$ $\Rightarrow a = 5.$

(E) có tiêu điểm F2(3; 0) nên c = 3

$\Rightarrow b = \sqrt{a^{2}-c^{2}}=4$ $\Rightarrow b = \sqrt{a^{2}-c^{2}}=4$

Vậy phương trình chính tắc của (E): $\frac{x^{2}}{25}+\frac{y^{2}}{16}=1$ $\frac{x^{2}}{25}+\frac{y^{2}}{16}=1$

Bài 7.23 trang 56

Lập phương trình chính tắc của parabol đi qua điểm M(2; 4).

Gợi ý đáp án

Phương trình parabol (P) có dạng: y² = 2px.

(P) đi qua M(2; 4) nên 4² = 2p.2

$\Rightarrow 2p =8$ $\Rightarrow 2p =8$

Vậy phương trình (P): y² = 8x.

Bài 7.24 trang 56

Có hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300 km. Tại cùng một thời điểm, hai trạm cùng phát tín hiệu với vận tốc 292 000 km/s để một tàu thủy thu và đo độ lệch thời gian. Tín hiệu từ A đến sớm hơn tín hiệu từ B là 0,0005 s. Từ thông tin trên, ta có thể xác định được tàu thủy thuộc đường hybebol nào? Viết phương trình chính tắc của hypebol đó theo đơn vị kilômét.

Gợi ý đáp án

Chọn hệ trục tọa độ Oxy sao cho A, B nằm trên trục Ox, tia Ox trùng với tia OB, O là trung điểm của AB. Nên tọa độ hai điểm là: A(-150; 0) và B(150; 0)

Khi đó vị trí tàu thủy là điểm M nằm trên hypebol có 2 tiêu điểm là A và B.

Tín hiệu từ A đến sớm hơn tín hiệu từ B là 0,0005 s nên ta có: |MA - MB| = 0,0005.292 000 = 146 km.

Gọi phương trình chính tắc của hypebol có dạng: $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ với a, b > 0.

Do $|MA - MB| = 146 = 2a \Leftrightarrow a = 73.$ $|MA - MB| = 146 = 2a \Leftrightarrow a = 73.$

Do hai tiêu điểm là: A(-150; 0) và B(150; 0) nên c = 150

$\Rightarrow b = \sqrt{c^{2}-a^{2}}=\sqrt{17171}$ $\Rightarrow b = \sqrt{c^{2}-a^{2}}=\sqrt{17171}$

Vậy phương trình chính tắc của hypebol cần tìm là: $\frac{x^{2}}{5329}$ $\frac{x^{2}}{5329}$

Bài 7.25 trang 56

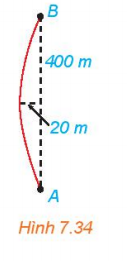
Khúc cua của một con đường có dạng hình parabol, điểm đầu vào khúc cua là A, điểm cuối là B, khoảng cách AB = 400m. Đỉnh parabol (P) của khúc của cách đường thẳng AB một khoảng 20 m và cách đều A, B.

a. Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 m trên thực tế.

b. Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 km trên thực tế.

Gợi ý đáp án

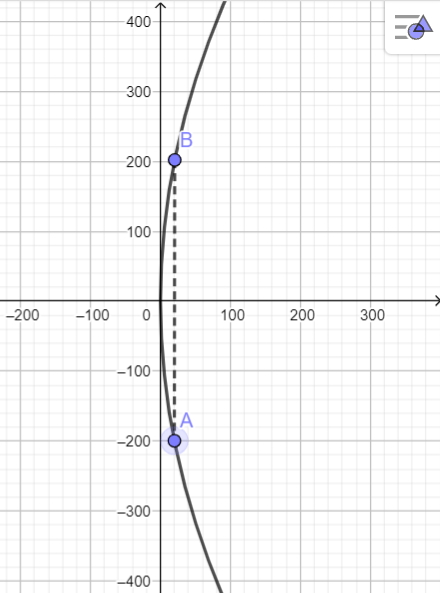
Chọn hệ trục tọa độ sao cho đỉnh của parabol trùng với gốc tọa độ O(0; 0) (như hình vẽ).

a. Nếu 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 m trên thực tế thì tọa độ các điềm là: A(20; -200) và B(20; 200) thuộc vào parabol có dạng y2 = 2px

Thay tọa độ điểm A và ta có: $2002 = 2p.20 \Rightarrow 2p = 2000$ $2002 = 2p.20 \Rightarrow 2p = 2000$

Vậy parabol có dạng: y² = 2000.x

b. Nếu 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 km trên thực tế thì tọa độ các điềm là: A(0,02; -0,2) và B(0,02; 0,2) thuộc vào parabol có dạng y² = 2px

Thay tọa độ điểm A và ta có: $0,22 = 2p.0,02 \Rightarrow 2p = 2$ $0,22 = 2p.0,02 \Rightarrow 2p = 2$

Vậy parabol có dạng: y² = 2.x

Chia sẻ bởi: