Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh Giải Toán lớp 7 trang 80, 81, 82 Tập 2 sách Cánh diều

Giải Toán 7 bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh Cánh diều là tài liệu vô cùng hữu ích giúp các em học sinh lớp 7 có thêm nhiều gợi ý tham khảo để giải các bài tập từ 1→4 trang 80, 81, 82 tập 2.

Giải bài tập Toán 7 Cánh diều tập 2 trang 80, 81, 82 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài, đồng thời là tư liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy sau đây là nội dung chi tiết Giải Toán 7 bài 4 trang 80, 81, 82 Cánh diều, mời các bạn cùng theo dõi.

Giải Toán 7 trang 80, 81, 82 Cánh diều - Tập 2

Bài 1

Cho Hình 42 có MN = QN, MP = QP. Chứng minh rằng \(\hat{MNP}\) = \(\hat{QNP }\)

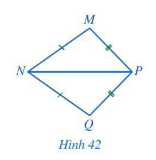
Xét ∆MNP và ∆QNP có:

MN = QN (theo giả thiết).

MP = QP (theo giả thiết).

NP chung.

Suy ra ∆MNP = ∆QNP(c - c - c).

Do đó \(\hat{MNP}\) = \(\hat{QNP }\) (2 góc tương ứng).

Bài 2 

Cho Hình 43 có AB = AD, \(\widehat {ABC} = \widehat {ADC} = 90^\circ\). Chứng minh \(\widehat {ACB} = \widehat {ACD}.\)

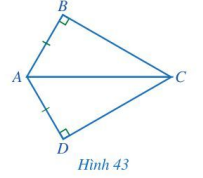
Gợi ý đáp án

Xét hai tam giác vuông ABC và ADC có: AB = AD, AC chung.

Nên \(\Delta ABC = \Delta ADC\) (cạnh huyền - cạnh góc vuông) nên \(\widehat {ACB} = \widehat {ACD}\) (2 góc tương ứng)

Bài 3 

Cho Hình 44 có AC = BD, \(\widehat {ABC} = \widehat {BAD} = 90^\circ\). Chứng minh AD = BC.

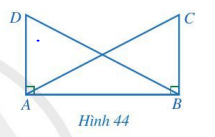
Gợi ý đáp án

Xét hai tam giác vuông DAB và CBA: AC = BD; AB chung.

Nên \(\Delta DAB = \Delta CBA\) (cạnh huyền - cạnh góc vuông)

Nên AD = BC ( 2 cạnh tương ứng)

Bài 4 

Cho hai tam giác ABC và MNP thỏa mãn: AB = MN, BC = NP, AC = MP, \(\widehat A = 65^\circ\) , \(\widehat N = 71^\circ\). Tính số đo các góc còn lại của hai tam giác.

Gợi ý đáp án

Tam giác ABC và tam giác MNP bằng nhau (có ba cặp cạnh bằng nhau: AB = MN, BC = NP, AC = MP). Nên các cặp góc tương ứng trong hai tam giác này bằng nhau: \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P.\)

Vậy \(\widehat A = \widehat M = 65^\circ ; \widehat B = \widehat N = 71^\circ ; \widehat C = \widehat P = 180^\circ  - 65^\circ  - 71^\circ  = 44^\circ\) (vì tổng ba góc trong một tam giác bằng 180°).