Toán 7 Bài 2: Tia phân giác của một góc Giải Toán lớp 7 trang 98 - Tập 1 sách Cánh diều

Tải về

Toán lớp 7 trang 99 Cánh diều tập 1 giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần Luyện tập vận dụng và 4 bài tập cuối bài Tia phân giác của một góc thuộc Chương 4: Góc - Đường thẳng song song được chính xác thuận tiện hơn.

Toán 7 Cánh diều tập 1 trang 99 hướng dẫn các em giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 7. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được. Vậy sau đây là trọn bộ tài liệu giải Toán 7 trang 99 Cánh diều tập 1 mời các bạn cùng theo dõi.

Toán 7 Bài 2: Tia phân giác của một góc

Phần Hoạt động

Hoạt động 1 trang 96 Toán 7 tập 1

Quan sát góc vuông xOy và tia Oz ở hình 25.

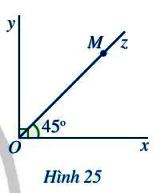
a) Mỗi điểm M (M khác O) thuộc tia Oz có phải là điểm trong của góc xOy hay không? Tia Oz có nằm trong góc xOy hay không?

b) Tính số đo góc yOz.

c) So sánh hai góc xOz và yOz.

Gợi ý đáp án

a) Điểm M không thuộc tia Ox, cũng không thuộc tia Oy và nằm bên trong góc xOy.

=> Điểm M (M khác O) thuộc tia Oz là điểm trong của góc xOy.

Tia Oz đi qua điểm M mà điểm M cũng nằm trong góc xOy.

=> Tia Oz nằm trong góc xOy.

Vậy điểm M (M khác O) thuộc tia Oz là điểm trong của góc xOy và tia Oz nằm trong góc xOy.

b) Tia Oz nằm trong góc xOy

=> Tia Oz nằm giữa hai tia Ox và Oy

=> $\widehat {xOz} + \widehat {yOz} = \widehat {xOy}$ $\widehat {xOz} + \widehat {yOz} = \widehat {xOy}$

=> $\widehat {yOz} = \widehat {xOy} - \widehat {xOz}$ $\widehat {yOz} = \widehat {xOy} - \widehat {xOz}$

=> $\widehat {yOz} = {90^0} - {45^0} = {45^0}$ $\widehat {yOz} = {90^0} - {45^0} = {45^0}$

c) Ta có: $\widehat {xOz} = {45^0};\widehat {yOz} = {45^0}$ $\widehat {xOz} = {45^0};\widehat {yOz} = {45^0}$

=> $\widehat {xOz} = \widehat {yOz}$ $\widehat {xOz} = \widehat {yOz}$

Hoạt động 2 trang 96 Toán 7 tập 1

Gợi ý đáp án

Để vẽ tia phân giác của góc xOy bằng thước thẳng và compa, ta làm như sau:

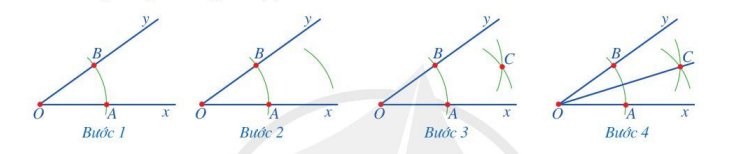
Bước 1: Trên tia Ox lấy điểm A bất kì (A khác O). Vẽ một phần đường tròn tâm O bán kính OA, cắt Oy tại điểm B.

Bước 2: Vẽ một phần đường tròn tâm A bán kính AO.

Bước 3: Vẽ một phần đường tròn tâm B bán kính AO, cắt phần đường tròn tâm A bán kính AO tại điểm C nằm trong góc xOy.

Bước 4: Vẽ tia OC, ta được tia phân giác của góc xOy.

Hình vẽ minh họa:

Phần Luyện tập vận dụng

Luyện tập 1 trang 97 Toán 7 tập 1

Kiểm tra lại bằng thước đo góc để thấy các góc xOC và góc yOC trong Hoạt động 2 là bằng nhau.

Gợi ý đáp án

Sử dụng thước đo góc kiểm tra lại các góc ta được kết quả:

Hai góc xOC và góc yOC có số đo bằng nhau

=> $\widehat {xOC} = \widehat {yOK}$ $\widehat {xOC} = \widehat {yOK}$

Luyện tập 2 trang 98 Toán 7 tập 1

Kiểm tra lại bằng thước đo góc để thấy các góc mIK và nIK trong Hoạt động 3 là bằng nhau.

Gợi ý đáp án

Sử dụng thước đo góc kiểm tra lại các góc ta được kết quả:

Hai góc mIK và nIK có số đo bằng nhau

=> $\widehat {mIk} = \widehat {nIK}$ $\widehat {mIk} = \widehat {nIK}$

Phần Bài tập

Bài 1 trang 99 SGK Toán 7 tập 1 Cánh diều

Để xác định phương hướng trên bản đồ hay trên thực địa, người ta thường xác định 8 hướng (Bắc, Nam, Đông, Tây, Đông Bắc, Đông Nam, Tây Nam, Tây Bắc) như Hình 29. Trong đó:

a) Tia OB là tia phân giác của những góc nào?

b) Tia OT là tia phân giác của những góc nào?

Gợi ý đáp án

a) Tia OB là tia phân giác của những góc xOu; góc TOĐ

b) Tia OT là tia phân giác của những góc yOu; góc BON

Bài 2 trang 99 SGK Toán 7 tập 1 Cánh diều

Trong Hình 30, tính số đo của $\widehat {mOp};\widehat {qOr};\widehat {pOq}$ $\widehat {mOp};\widehat {qOr};\widehat {pOq}$

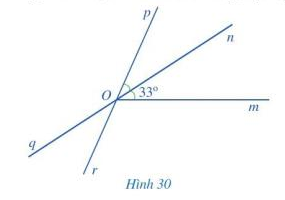
Gợi ý đáp án

Vì On là tia phân giác của $\widehat {mOp}$ $\widehat {mOp}$ nên $\widehat {mOp} = 2.\widehat {mOn} = 2.33^\circ = 66^\circ$ $\widehat {mOp} = 2.\widehat {mOn} = 2.33^\circ = 66^\circ$

Vì $\widehat {qOr} = \widehat {mOn}$ $\widehat {qOr} = \widehat {mOn}$ ( 2 góc đối đỉnh), mà $\widehat {mOn} = 33^\circ \Rightarrow \widehat {qOr} = 33^\circ$ $\widehat {mOn} = 33^\circ \Rightarrow \widehat {qOr} = 33^\circ$

Vì $\widehat {pOq} + \widehat {qOr} = 180^\circ$ $\widehat {pOq} + \widehat {qOr} = 180^\circ$( 2 góc kề bù) nên $\widehat {pOq} + 33^\circ = 180^\circ \Rightarrow \widehat {pOq} = 180^\circ - 33^\circ = 147^\circ$ $\widehat {pOq} + 33^\circ = 180^\circ \Rightarrow \widehat {pOq} = 180^\circ - 33^\circ = 147^\circ$

Vậy $\widehat {mOp} = 66^\circ ;\widehat {qOr} = 33^\circ ;\widehat {pOq} = 147^\circ$ $\widehat {mOp} = 66^\circ ;\widehat {qOr} = 33^\circ ;\widehat {pOq} = 147^\circ$

Bài 3 trang 99 SGK Toán 7 tập 1 Cánh diều

Ở Hình 31 có góc vuông xOy, các tia On, Oz, Om nằm trong góc đó và $\widehat {xOn} = \widehat {nOz},\widehat {yOm} = \widehat {mOz}.$ $\widehat {xOn} = \widehat {nOz},\widehat {yOm} = \widehat {mOz}.$

a) Các tia Om, On có tương ứng là tia phân giác của góc yOz và xOz hay không?

b) Cho biết số đo góc mOn.

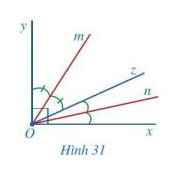
Gợi ý đáp án

a) Các tia Om, On tương ứng là tia phân giác của góc yOz và xOz vì:

Tia Om nằm trong góc yOz và $\widehat {yOm} = \widehat {mOz}$ $\widehat {yOm} = \widehat {mOz}$

Tia On nằm trong góc xOz và $\widehat {xOn} = \widehat {nOz}$ $\widehat {xOn} = \widehat {nOz}$

b) Vì các tia Om, On tương ứng là tia phân giác của góc yOz và xOz nên: $\widehat {yOm} = \widehat {mOz} = \frac{1}{2}.\widehat {yOz};\widehat {xOn} = \widehat {nOz} = \frac{1}{2}.\widehat {xOz}$ $\widehat {yOm} = \widehat {mOz} = \frac{1}{2}.\widehat {yOz};\widehat {xOn} = \widehat {nOz} = \frac{1}{2}.\widehat {xOz}$

Mà tia Oz nằm trong góc xOy nên $\widehat {yOz} + \widehat {xOz} = \widehat {xOy}$ $\widehat {yOz} + \widehat {xOz} = \widehat {xOy}$

$\Rightarrow \widehat {mOz} + \widehat {zOn} = \frac{1}{2}.\widehat {yOz} + \frac{1}{2}.\widehat {xOz} = \frac{1}{2}.\widehat {xOy}$ $\Rightarrow \widehat {mOz} + \widehat {zOn} = \frac{1}{2}.\widehat {yOz} + \frac{1}{2}.\widehat {xOz} = \frac{1}{2}.\widehat {xOy}$

Mà tia Oz nằm trong góc mOn nên $\widehat {mOz} + \widehat {zOn} = \widehat {mOn}$ $\widehat {mOz} + \widehat {zOn} = \widehat {mOn}$ và $\widehat {xOy} = 90^\circ \Rightarrow \widehat {mOn} = \frac{1}{2}.90^\circ = 45^\circ$ $\widehat {xOy} = 90^\circ \Rightarrow \widehat {mOn} = \frac{1}{2}.90^\circ = 45^\circ$