Toán 7 Bài 1: Tổng các góc của một tam giác Giải Toán lớp 7 trang 70, 71, 72 - Tập 2 sách Cánh diều

Giải Toán 7 Bài 1: Tổng các góc của một tam giác Cánh diều là tài liệu vô cùng hữu ích giúp các em học sinh lớp 7 có thêm nhiều gợi ý tham khảo để giải các bài tập từ 1→7 trang 70, 71, 72 tập 2.

Giải SGK Toán 7 bài 1 chương 7: Tam giác giúp các em tham khảo phương pháp giải toán, những kinh nghiệm trong quá trình tìm tòi ra lời giải. Giải bài tập Toán 7 tập 2 trang 70, 71, 72 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài, đồng thời là tư liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập.

Bài 1

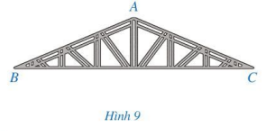
Một khung thép có dạng hình tam giác ABC với số đo các góc ở đỉnh B và đỉnh C cùng bằng 23° (Hình 9). Tính số đo của góc ở đỉnh A.

Gợi ý đáp án

Ta có: \(\widehat A + 23^\circ  + 23^\circ  = 180^\circ\)

Suy ra: \(\widehat A = 180^\circ  - 23^\circ  - 23^\circ  = 134^\circ\)

Bài 2

Hình 10 biểu diễn một chiếc cầu trượt gồm máng trượt và thang leo. Tính độ nghiêng của máng trượt so với phương thẳng đứng, biết rằng độ nghiêng của máng trượt so với mặt đất là 38°.

Gợi ý đáp án

Chiếc cầu trượt được minh họa và đặt tên các đỉnh như hình dưới đây:

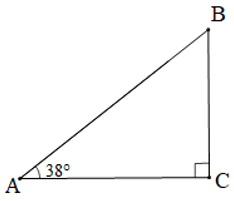
Tam giác ABC vuông tại C

\(\Rightarrow \widehat{A} + \widehat{B} = 90^o\) (trong tam giác vuông, tổng hai góc nhọn bằng 90 ° ).

\(\Rightarrow\widehat{B}=90^o-\widehat{A}=90^o-38^o=52^o\)

Vậy độ nghiêng của máng trượt so với phương thẳng đứng là 52⁰.

Bài 3

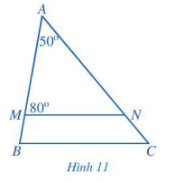
Trong Hình 11, MN // BC. Tính số đo góc C.

Gợi ý đáp án

Vì MN // BC nên \(\widehat{ANM}=\widehat{C}\) (2 góc đồng vị)

Áp dụng định lí tổng ba góc trong tam giác AMN có:

\(\widehat{A}+\widehat{M} + \widehat{ANM}=180^0\)

\(\Rightarrow  \widehat{ANM}= 180^\circ  - 50^\circ  - 80^\circ  = 50^\circ\).

Vậy \(\widehat{C}=50^0\)

Bài 4

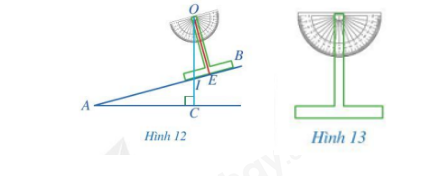
Hình 12 biểu diễn mặt cắt đứng của một đường lên dốc AB. Để đo độ dốc của con đường biểu diễn bởi góc nhọn BAC tạo bới đường thẳng AB và phương nằm ngang AC, người ta làm như sau:

- Làm một thước chữ T như Hình 13;

- Đặt thước chữ T dọc theo cạnh AB như Hình 12, OE \bot AB;

- Buộc một sợi dây vào chân O của thước chữ T và buộc một vật nặng vào đầu dây còn lại, sau đó thả vật nặng để sợi dây có phương thẳng đứng (trong xây dựng gọi là thả dây dọi);

- Tính góc BAC, biết rằng dây dọi OI tạo với trục OE của thước chữ T một góc 15°.

Gợi ý đáp án

Ta có, trong tam giác OIE:\(\widehat I + 15^\circ  + 90^\circ  = 180^\circ\).

Suy ra: \(\widehat {OIE} = \widehat {AIC} = 180^\circ  - 90^\circ  - 15^\circ  = 75^\circ\).

Vậy góc BAC bằng: \(90^\circ  - 75^\circ  = 15^\circ\).