Toán 7 Bài 3: Hai đường thẳng song song Giải Toán lớp 7 trang 104 - Tập 1 sách Cánh diều

Bài trước

Mục lục

Bài sau

Giải Toán lớp 7 trang 104 tập 1 Cánh diều giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần Hoạt động và 3 bài tập cuối bài Hai đường thẳng song song được nhanh chóng thuận tiện hơn.

Toán 7 Cánh diều tập 1 trang 104 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 7. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được. Vậy sau đây là trọn bộ tài liệu giải Toán 7 trang 104 Cánh diều tập 1 mời các bạn cùng theo dõi.

Toán 7 Bài 3: Hai đường thẳng song song

Phần Hoạt động

Hoạt động 1 trang 100 Toán 7 tập 1

Đọc kĩ các nội dung sau:

Ở Hình 34, đường thẳng c cắt hai đường thẳng a, b lần lượt tại điểm A, B.

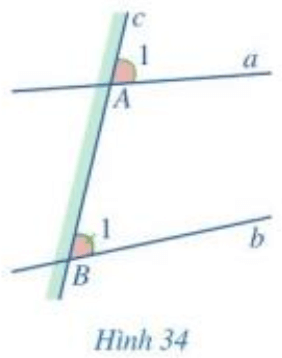
a) Quan sát vị trí của mỗi góc A₁ và B₁ ở Hình 34, ta thấy:

- Góc A₁ và góc B₁ ở “cùng một phía” của đường thẳng c;

- Góc A₁ ở “phía trên” đường thẳng a;

Góc B₁ ở “phía trên” đường thẳng b.

Hai góc A₁ và B₁ ở vị trí như thế gọi là hai góc đồng vị.

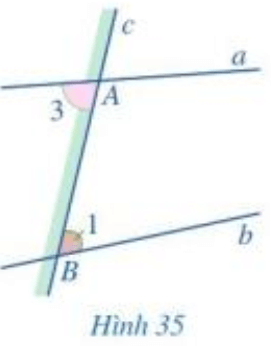
Quan sát vị trí của mỗi góc A₃ và B₁ ở Hình 35, ta thấy:

- Góc A₃ và góc B₁ ở “hai phía” của đường thẳng c.

- Góc A₃ ở “phía dưới” đường thẳng a;

Góc B₁ ở “phía trên” đường thẳng b.

Hai góc A₃ và B₁ ở vị trí như thế gọi là hai góc so le trong.

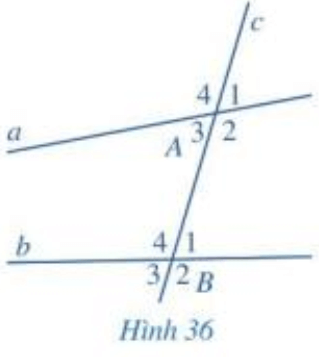
Tương tự, trong Hình 36 ta cũng có:

- Các cặp góc A₁ và B₁, A₂ và B₂, A₃ và B₃, A₄ và B₄ là các cặp góc đồng vị;

- Cặp góc A₃ và B₁, A₂ và B₄ là cặp góc so le trong.

Lời giải:

Học sinh đọc và làm theo các yêu cầu của hoạt động.

Hoạt động 2 trang 101 Toán 7 tập 1

Quan sát các hình 38a, 38b, 38c và đoán xem các đường thẳng nào song song với nhau:

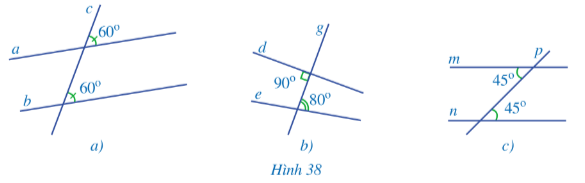
Phần Bài tập

Bài 1 trang 104 Toán 7 tập 1

Quan sát hình 44, biết a // b.

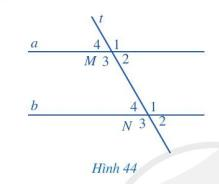
a) So sánh $\widehat {{M_1}}$ $\widehat {{M_1}}$ và $\widehat {{N_3}}; \widehat {{M_4}}$ $\widehat {{N_3}}; \widehat {{M_4}}$ và $\widehat {{N_2}}$ $\widehat {{N_2}}$ ( mỗi cặp góc M1 và N3, M4 và N2 gọi là một cặp góc so le ngoài)

b) Tính: $\widehat {{M_2}} + \widehat {{N_1}}$ $\widehat {{M_2}} + \widehat {{N_1}}$ và $\widehat {{M_3}} + \widehat {{N_4}}$ $\widehat {{M_3}} + \widehat {{N_4}}$ ( mỗi cặp góc M2 và N1, M3 và N4 gọi là một cặp góc trong cùng phía)

Gợi ý đáp án

a) Vì a // b nên $\widehat {{M_1}} = \widehat {{N_1}}; \widehat {{M_4}} = \widehat {{N_4}}$ $\widehat {{M_1}} = \widehat {{N_1}}; \widehat {{M_4}} = \widehat {{N_4}}$ ( 2 góc đồng vị) mà $\widehat {{N_3}} = \widehat {{N_1}} ; \widehat {{N_4}} = \widehat {{N_2}}$ $\widehat {{N_3}} = \widehat {{N_1}} ; \widehat {{N_4}} = \widehat {{N_2}}$ ( 2 góc đối đỉnh) nên $\widehat {{M_1}} =\widehat {{N_3}}; \widehat {{M_4}} =\widehat {{N_2}}$ $\widehat {{M_1}} =\widehat {{N_3}}; \widehat {{M_4}} =\widehat {{N_2}}$

b) Vì a // b nên $\widehat {{M_2}} = \widehat {{N_2}};\widehat {{M_3}} = \widehat {{N_3}}$ $\widehat {{M_2}} = \widehat {{N_2}};\widehat {{M_3}} = \widehat {{N_3}}$ ( 2 góc đồng vị), mà $\widehat {{N_1}} + \widehat {{N_2}} = 180^\circ ;\widehat {{N_3}} + \widehat {{N_4}} = 180^\circ$ $\widehat {{N_1}} + \widehat {{N_2}} = 180^\circ ;\widehat {{N_3}} + \widehat {{N_4}} = 180^\circ$( 2 góc kề bù) nên $\widehat {{M_2}} + \widehat {{N_1}} = 180^\circ ; \widehat {{M_3}} + \widehat {{N_4}}= 180^\circ$ $\widehat {{M_2}} + \widehat {{N_1}} = 180^\circ ; \widehat {{M_3}} + \widehat {{N_4}}= 180^\circ$

Bài 2 trang 104 Toán 7 tập 1

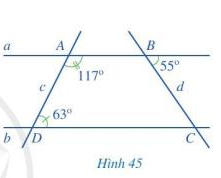
Quan sát Hình 45.

a) Vì sao hai đường thẳng a và b song song với nhau?

b) Tính số đo góc BCD.

Gợi ý đáp án

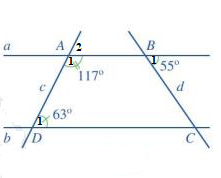
a) Vì $\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ$ $\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ$( 2 góc kề bù) nên $117^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 180^\circ - 117^\circ = 63^\circ$ $117^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 180^\circ - 117^\circ = 63^\circ$

Vì $\widehat {{A_2}} = \widehat {{D_1}}$ $\widehat {{A_2}} = \widehat {{D_1}}$ ( cùng bằng 63 độ)

Mà 2 góc này ở vị trí đồng vị

$\Rightarrow a // b$ $\Rightarrow a // b$( đpcm)

b) Vì a // b nên $\widehat {{B_1}} = \widehat {BCD}$ $\widehat {{B_1}} = \widehat {BCD}$ ( 2 góc so le trong), mà $\widehat {{B_1}} = 55^\circ$ $\widehat {{B_1}} = 55^\circ$

Bài 3 trang 104 Toán 7 tập 1

Để đảm bảo an toàn khi đi lại trên cầu thang của ngôi nhà, người ta phải làm lan can. Phía trên của lan can có tay vịn làm chỗ dựa để khi lên xuống cầu thang được thuận tiện. Phía dưới tay vịn là các thanh trụ song song với nhau và các thanh sườn song song với nhau. Để đảm bảo chắc chắn thì các thanh trụ của lan can được gắn vuông góc cố định xuống bậc cầu thang.

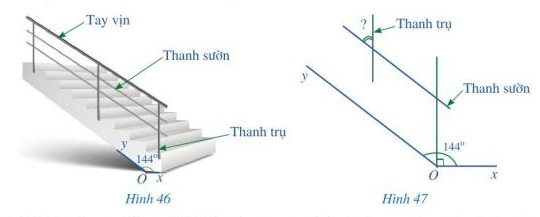
Trong Hình 46, góc xOy bằng $144^\circ$ $144^\circ$. Hỏi góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can là bao nhiêu độ?

Gợi ý đáp án

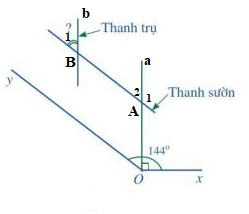
Vì AB // Oy nên $\widehat {xOy} = \widehat {{A_1}}$ $\widehat {xOy} = \widehat {{A_1}}$ ( 2 góc đồng vị), mà $\widehat {xOy} = 144^\circ \Rightarrow \widehat {{A_1}} = 144^\circ$ $\widehat {xOy} = 144^\circ \Rightarrow \widehat {{A_1}} = 144^\circ$

Vì $\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ$ $\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ$( 2 góc kề bù) nên $\widehat {{A_2}} + 144^\circ = 180^\circ \Rightarrow \widehat {{A_2}} = 180^\circ - 144^\circ = 36^\circ$ $\widehat {{A_2}} + 144^\circ = 180^\circ \Rightarrow \widehat {{A_2}} = 180^\circ - 144^\circ = 36^\circ$

Vì a // b nên $\widehat {{B_1}} = \widehat {{A_2}}$ $\widehat {{B_1}} = \widehat {{A_2}}$ ( 2 góc đồng vị), mà $\widehat {{A_2}} = 36^\circ \Rightarrow \widehat {{B_1}} = 36^\circ$ $\widehat {{A_2}} = 36^\circ \Rightarrow \widehat {{B_1}} = 36^\circ$

Lý thuyết Hai đường thẳng song song

1. Khái niệm hai đường thẳng song song

Hai đường thẳng song song (trong mặt phẳng) là hai đường thẳng không có điểm chung.

Kí hiệu a//b.

- Hai đường thẳng phân biệt thì hoặc cắt nhau hoặc song song.

2. Dấu hiệu nhận biết hai đường thẳng song song

+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song.

+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song.

+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau thì hai đường thẳng song song.

Ngoài ra ta còn có dấu hiệu: Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le ngoài bằng nhau thì hai đường thẳng song song.

Chia sẻ bởi: