| |
Toán 7 Bài 1: Số vô tỉ. Căn bậc hai số học Giải Toán lớp 7 trang 35 - Tập 1 sách Cánh diều
Bài trước
Giải Toán lớp 7 trang 35 tập 1 Cánh diều giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần Luyện tập vận dụng và 5 bài tập thuộc bài Số vô tỉ - Căn bậc hai số học được nhanh chóng và dễ dàng hơn.
Toán 7 Cánh diều tập 1 trang 35 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 7. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 7 trang 35 Cánh diều mời các bạn cùng theo dõi.
Toán 7 Bài 1: Số vô tỉ. Căn bậc hai số học
Phần Luyện tập vận dụng
Luyện tập 1 trang 33 Toán 7 tập 1
Phát biểu “Mỗi số vô tỉ đều không thể là số hữu tỉ” là đúng hay sai? Vì sao?
Gợi ý đáp án
Phát biểu trên là đúng vì mỗi số vô tỉ đều được viết dưới dạng số thập phân vô hạn không tuần hoàn, còn các số hữu tỉ thì được viết dưới dạng các số thập phân hữu hạn hoặc vô hạn tuần hoàn.
Do vậy nếu một số là vô tỉ thì số đó không thể là số hữu tỉ.
Phần Hoạt động
Hoạt động 1 trang 33 Toán 7 tập 1
Viết phân số ![]() \(\frac{1}{3}\) dưới dạng số thập phân vô hạn tuần hoàn.
\(\frac{1}{3}\) dưới dạng số thập phân vô hạn tuần hoàn.
Gợi ý đáp án
Thực hiện phép chia 1 cho 3 như sau:
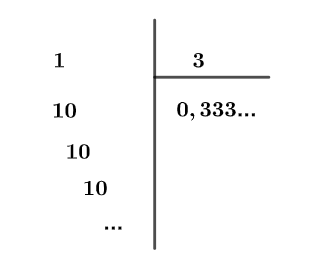
Suy ra ![]() \(\frac{1}{3} = 0,333.... = 0,\left( 3 \right)\)
\(\frac{1}{3} = 0,333.... = 0,\left( 3 \right)\)
Số thập phân 0,333… có vô số chữ số khác 0 ở phần thập phân của số đó được gọi là số thập phân vô hạn.
Hoạt động 2 trang 33 Toán 7 tập 1
Tính:
|
a) 32 |
b) (0,4)2 |
Gợi ý đáp án
Ta có:
a) 32 = 3.3 = 9
b) (0,4)2 = 0,4 . 0.4 = 0,16
Số dương 3 thỏa mãn 32 = 9, ta gọi 3 là căn bậc hai số học của 9
Tương tự như vậy, số dương 0,4 thỏa mãn (0.4)2 = 0,16 ta gọi 0,4 là căn bậc hai số học của 0,16.
Hoạt động 3 trang 34 Toán 7 tập 1
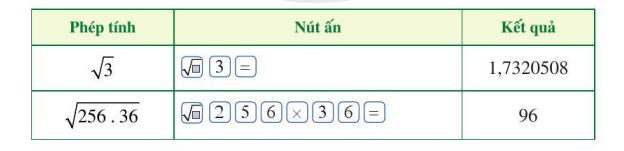
Ta có thể tính được giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số dương bằng máy tính cầm tay. Chẳng hạn để tính ![]() \(\sqrt 3 ;\sqrt {256.36}\) , ta sử dụng nút dấu căn bậc hai số học và làm như sau:
\(\sqrt 3 ;\sqrt {256.36}\) , ta sử dụng nút dấu căn bậc hai số học và làm như sau:
Gợi ý đáp án
Thực hiện các bước theo hướng dẫn
Phần Bài tập
Bài 1 trang 35 Toán 7 tập 1
a) Đọc các số sau: ![]() \(\sqrt {15} ;\sqrt {27,6} ;\sqrt {0,82}\)
\(\sqrt {15} ;\sqrt {27,6} ;\sqrt {0,82}\)
b) Viết các số sau: căn bậc hai số học của 39; căn bậc hai số học của ![]() \(\frac{9}{{11}}\); căn bậc hai số học của
\(\frac{9}{{11}}\); căn bậc hai số học của ![]() \(\frac{{89}}{{27}}\)
\(\frac{{89}}{{27}}\)
Gợi ý đáp án
a)![]() \(\sqrt {15}\) đọc là: căn bậc hai số học của mười lăm
\(\sqrt {15}\) đọc là: căn bậc hai số học của mười lăm
![]() \(\sqrt {27,6}\) đọc là: căn bậc hai số học của hai mươi bảy phẩy sáu
\(\sqrt {27,6}\) đọc là: căn bậc hai số học của hai mươi bảy phẩy sáu
![]() \(\sqrt {0,82}\)đọc là: căn bậc hai số học của không phẩy tám mươi hai
\(\sqrt {0,82}\)đọc là: căn bậc hai số học của không phẩy tám mươi hai
b) Căn bậc hai số học của 39 viết là: ![]() \(\sqrt {39}\)
\(\sqrt {39}\)
Căn bậc hai số học của ![]() \(\frac{9}{{11}}\) viết là:
\(\frac{9}{{11}}\) viết là: ![]() \(\sqrt {\frac{9}{{11}}}\)
\(\sqrt {\frac{9}{{11}}}\)
Căn bậc hai số học của ![]() \(\frac{{89}}{{27}}\) viết là:
\(\frac{{89}}{{27}}\) viết là: ![]() \(\sqrt {\frac{{89}}{{27}}}\)
\(\sqrt {\frac{{89}}{{27}}}\)
Bài 2 trang 35 Toán 7 tập 1
Chứng tỏ rằng:
a) Số 0,8 là căn bậc hai số học của số 0,64
b) Số -11 không phải là căn bậc hai số học của số 121
c) Số 1,4 là căn bậc hai số học của số 1,96 nhưng –1,4 không phải là căn bậc hai số học của số 1,96.
Gợi ý đáp án
a) Vì 0,8 > 0 và ![]() \(0,{8^2}\) = 0,64 nên số 0,8 là căn bậc hai số học của số 0,64
\(0,{8^2}\) = 0,64 nên số 0,8 là căn bậc hai số học của số 0,64
b) Vì tuy ![]() \({( - 11)^2} = 121\) nhưng -11 < 0 nên số -11 không phải là căn bậc hai số học của số 121
\({( - 11)^2} = 121\) nhưng -11 < 0 nên số -11 không phải là căn bậc hai số học của số 121
c) Vì ![]() \(1,{4^2} = 1,96\) và 1,4 > 0 nên số 1,4 là căn bậc hai số học của số 1,96
\(1,{4^2} = 1,96\) và 1,4 > 0 nên số 1,4 là căn bậc hai số học của số 1,96
Nhưng vì -1,4 < 0 nên –1,4 không phải là căn bậc hai số học của số 1,96.
Bài 3 trang 35 Toán 7 tập 1
Tìm số thích hợp cho vào chỗ trống

Gợi ý đáp án

Bài 4 trang 35 Toán 7 tập 1
Tính giá trị của biểu thức:
![]() \(a)\sqrt {0,49} + \sqrt {0,64} ;\)
\(a)\sqrt {0,49} + \sqrt {0,64} ;\)
![]() \(b)\sqrt {0,36} - \sqrt {0,81} ;\)
\(b)\sqrt {0,36} - \sqrt {0,81} ;\)
![]() \(c)8.\sqrt 9 - \sqrt {64} ;\)
\(c)8.\sqrt 9 - \sqrt {64} ;\)
![]() \(d)0,1.\sqrt {400} + 0,2.\sqrt {1600}\)
\(d)0,1.\sqrt {400} + 0,2.\sqrt {1600}\)
Gợi ý đáp án
 \(\begin{array}{l}a)\sqrt {0,49} + \sqrt {0,64} = 0,7 + 0,8 = 1,5;\\b)\sqrt {0,36} - \sqrt {0,81} = 0,6 - 0,9 = - 0,3;\\c)8.\sqrt 9 - \sqrt {64} = 8.3 - 8 = 24 - 8 = 16;\\d)0,1.\sqrt {400} + 0,2.\sqrt {1600} = 0,1.20 + 0,2.40 = 2 + 8 = 10\end{array}\)
\(\begin{array}{l}a)\sqrt {0,49} + \sqrt {0,64} = 0,7 + 0,8 = 1,5;\\b)\sqrt {0,36} - \sqrt {0,81} = 0,6 - 0,9 = - 0,3;\\c)8.\sqrt 9 - \sqrt {64} = 8.3 - 8 = 24 - 8 = 16;\\d)0,1.\sqrt {400} + 0,2.\sqrt {1600} = 0,1.20 + 0,2.40 = 2 + 8 = 10\end{array}\)
Bài 5 trang 35 Toán 7 tập 1
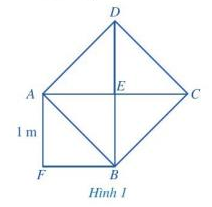
Quan sát Hình 1, ở đó hình vuông AEBF có cạnh bằng 1 m, hình vuông ABCD có cạnh AB là một đường chéo của hình vuông AEBF.
a) Tính diện tích của hình vuông ABCD.
b) Tính độ dài đường chéo AB.
Gợi ý đáp án
a) Ta có: ![]() \({S_{ABCD}} = 4.{S_{AEB}} = 4. \frac{1}{2}.1.1 = 2 (cm2)\)
\({S_{ABCD}} = 4.{S_{AEB}} = 4. \frac{1}{2}.1.1 = 2 (cm2)\)
b) ![]() \(AB = \sqrt {S{}_{ABCD}} = \sqrt 2\) (cm)
\(AB = \sqrt {S{}_{ABCD}} = \sqrt 2\) (cm)
Lý thuyết Số vô tỉ - Căn bậc hai số học
1. Số vô tỉ
+ Số vô tỉ là số được viết dưới dạng số thập phân vô hạn không tuần hoàn.
+ Tập hợp các số vô tỉ được kí hiệu là I.
Ví dụ:
+ π = 3,141592653 là số vô tỉ
+ 2,1543921 là số vô tỉ.
2. Khái niệm về căn bậc hai
Căn bậc hai của một số a không âm là số x sao cho
Chú ý:
• Nếu a > 0 thì a có hai căn bậc hai:
+ Căn bậc hai dương của a, được kí hiệu là √a.
+ Căn bậc hai âm của a, được kí hiệu là -√a.
• Số 0 có đúng một căn bậc hai là 0.
• Số âm không có căn bậc hai.
Liên kết tải về
Toán 7 Bài 1: Số vô tỉ. Căn bậc hai số học
359,4 KB
Tải về
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
1 Bình luận
Sắp xếp theo
-
 Lã HàThích · Phản hồi · 0 · 17/10/23
Lã HàThích · Phản hồi · 0 · 17/10/23
Chủ đề liên quan
Tìm bài trong mục này
Đóng
Chỉ thành viên Download Pro tải được nội dung này!
Download Pro - Tải nhanh, website không quảng cáo!
Tìm hiểu thêm












 Toán 7 Kết nối tri thức
Toán 7 Kết nối tri thức
 Toán 7 Chân trời sáng tạo
Toán 7 Chân trời sáng tạo
 Toán 7 Cánh Diều
Toán 7 Cánh Diều
 Soạn Văn 7 Chân trời sáng tạo
Soạn Văn 7 Chân trời sáng tạo
 Soạn Văn 7 Cánh Diều
Soạn Văn 7 Cánh Diều
 Soạn Văn 7 Kết nối tri thức
Soạn Văn 7 Kết nối tri thức
 Tiếng Anh 7 Global Success
Tiếng Anh 7 Global Success
 Tiếng Anh 7 Explore English
Tiếng Anh 7 Explore English
 Tiếng Anh 7 - iLearn Smart World
Tiếng Anh 7 - iLearn Smart World









