Toán 7 Bài tập cuối chương 1 - Cánh diều Giải Toán lớp 7 trang 30 - Tập 1

Bài trước

Mục lục

Bài sau

Bài tập cuối chương 1 Toán 7 Cánh diều là tài liệu vô cùng hữu ích, được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 7 tập 1.

Toán lớp 7 trang 30, 31 tập 1 Cánh diều hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 7. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán lớp 7 trang 30 tập 1 Cánh diều mời các bạn cùng theo dõi.

Bài tập cuối chương 1 Toán 7 Cánh diều

Giải Toán 7 trang 30, 31 Cánh diều - Tập 1

Giải Toán 7 trang 30, 31 Cánh diều - Tập 1

Bài 1 trang 30 Toán 7 tập 1

a) Sắp xếp các số sau theo thứ tự tăng dần: $0,5;1;\frac{{ - 2}}{3}.$ $0,5;1;\frac{{ - 2}}{3}.$

b) Trong ba điểm A, B, C trên trục số dưới đây có một điểm biểu diễn số hữu tỉ 0,5. Hãy xác định điểm đó.

Phương pháp giải

- Với hai số hữu tỉ a, b bất kì, ta luôn có hoặc a = b hoặc a < b hoặc a > b.

Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).

- Trên trục số nếu a < b thì điểm a nằm trước điểm b.

Gợi ý đáp án

a) Ta có $\frac{{ - 2}}{3} < 0,5 < 1$ $\frac{{ - 2}}{3} < 0,5 < 1$ nên:

Sắp xếp các số đã cho theo thứ tự tăng dần là: $\frac{{ - 2}}{3};\,0,5;\,1$ $\frac{{ - 2}}{3};\,0,5;\,1$

b) Số 0,5 nằm giữa số 0 và số 1

=> Điểm B biểu diễn số hữu tỉ 0,5.

Bài 2 trang 30 Toán 7 tập 1

Tính:

$a)5\frac{3}{4}.\frac{{ - 8}}{9};$ $a)5\frac{3}{4}.\frac{{ - 8}}{9};$

$b)3\frac{3}{4}:2\frac{1}{2}$ $b)3\frac{3}{4}:2\frac{1}{2}$

$c)\frac{{ - 9}}{5}:\frac{1}{2}$ $c)\frac{{ - 9}}{5}:\frac{1}{2}$

$d){\left( {1,7} \right)^{2023}}:{\left( {1,7} \right)^{2021}}.$ $d){\left( {1,7} \right)^{2023}}:{\left( {1,7} \right)^{2021}}.$

Phương pháp giải

Quy tắc dấu ngoặc

+ Khi bỏ dấu ngoặc có dấu (+) đằng trước, ta giữ nguyên dầu của các số trong dấu ngoặc

+ Khi bỏ dấu ngoặc có dấu (-) đằng trước ta phải đổi dấu của các số hạng trong dấu ngoặc: Dấu (+) đổi thành dấu (-), dấu (-) đổi thành dấu (+)

am . an = am + n

am : an = am – n

x0 = 1

(xm)n = xm . n

Gợi ý đáp án

$a)5\frac{3}{4}.\frac{{ - 8}}{9} = \frac{{23}}{4}.\frac{{ - 8}}{9} = \frac{{ - 46}}{9};$ $a)5\frac{3}{4}.\frac{{ - 8}}{9} = \frac{{23}}{4}.\frac{{ - 8}}{9} = \frac{{ - 46}}{9};$

$b)3\frac{3}{4}:2\frac{1}{2} = \frac{{15}}{4}:\frac{5}{2} = \frac{{15}}{4}.\frac{2}{5} = \frac{3}{2}$ $b)3\frac{3}{4}:2\frac{1}{2} = \frac{{15}}{4}:\frac{5}{2} = \frac{{15}}{4}.\frac{2}{5} = \frac{3}{2}$

$c)\frac{{ - 9}}{5}:\frac{1}{2} = \frac{{ - 9}}{5}.2 = \frac{{ - 18}}{5}$ $c)\frac{{ - 9}}{5}:\frac{1}{2} = \frac{{ - 9}}{5}.2 = \frac{{ - 18}}{5}$

$d){\left( {1,7} \right)^{2023}}:{\left( {1,7} \right)^{2021}} = {\left( {1,7} \right)^{2023 - 2021}} = {\left( {1,7} \right)^2} = 2,89.$ $d){\left( {1,7} \right)^{2023}}:{\left( {1,7} \right)^{2021}} = {\left( {1,7} \right)^{2023 - 2021}} = {\left( {1,7} \right)^2} = 2,89.$

Bài 3 trang 30 Toán 7 tập 1

Tính một cách hợp lí:

$a)\frac{{ - 5}}{{12}} + \left( { - 3,7} \right) - \frac{7}{{12}} - 6,3; b)2,8.\frac{{ - 6}}{{13}} - 7,2 - 2,8.\frac{7}{{13}}$ $a)\frac{{ - 5}}{{12}} + \left( { - 3,7} \right) - \frac{7}{{12}} - 6,3; b)2,8.\frac{{ - 6}}{{13}} - 7,2 - 2,8.\frac{7}{{13}}$

Phương pháp giải

Quy tắc dấu ngoặc

+ Khi bỏ dấu ngoặc có dấu (+) đằng trước, ta giữ nguyên dầu của các số trong dấu ngoặc

a + (b + c) = a + b + c

a + (b – c) = a + b – c

+ Khi bỏ dấu ngoặc có dấu (-) đằng trước ta phải đổi dấu của các số hạng trong dấu ngoặc: Dấu (+) đổi thành dấu (-), dấu (-) đổi thành dấu (+)

a – (b + c) = a – b – c

a – (b – c) = a – b + c

Gợi ý đáp án

$\begin{array}{l}\frac{{ - 5}}{{12}} + \left( { - 3,7} \right) - \frac{7}{{12}} - 6,3\\ = \left( {\frac{{ - 5}}{{12}} - \frac{7}{{12}}} \right) - \left( {3,7 + 6,3} \right)\\ = - 1 - 10 = - 11\end{array}$ $\begin{array}{l}\frac{{ - 5}}{{12}} + \left( { - 3,7} \right) - \frac{7}{{12}} - 6,3\\ = \left( {\frac{{ - 5}}{{12}} - \frac{7}{{12}}} \right) - \left( {3,7 + 6,3} \right)\\ = - 1 - 10 = - 11\end{array}$

$\begin{array}{l}2,8.\frac{{ - 6}}{{13}} - 7,2 - 2,8.\frac{7}{{13}}\\ = 2,8.\left( {\frac{{ - 6}}{{13}} - \frac{7}{{13}}} \right) - 7,2\\ = 2,8.\left( { - 1} \right) - 7,2\\ = - 2,8 - 7,2 = - 10\end{array}$ $\begin{array}{l}2,8.\frac{{ - 6}}{{13}} - 7,2 - 2,8.\frac{7}{{13}}\\ = 2,8.\left( {\frac{{ - 6}}{{13}} - \frac{7}{{13}}} \right) - 7,2\\ = 2,8.\left( { - 1} \right) - 7,2\\ = - 2,8 - 7,2 = - 10\end{array}$

Bài 4 trang 30 Toán 7 tập 1

Tính:

$a)0,3 - \frac{4}{9}:\frac{4}{3} \cdot \frac{6}{5} + 1;$ $a)0,3 - \frac{4}{9}:\frac{4}{3} \cdot \frac{6}{5} + 1;$

$b){\left( {\frac{{ - 1}}{3}} \right)^2} - \frac{3}{8}:{(0,5)^3} - \frac{5}{2} \cdot ( - 4);$ $b){\left( {\frac{{ - 1}}{3}} \right)^2} - \frac{3}{8}:{(0,5)^3} - \frac{5}{2} \cdot ( - 4);$

$c)1 + 2:\left( {\frac{2}{3} - \frac{1}{6}} \right) \cdot ( - 2,25)$ $c)1 + 2:\left( {\frac{2}{3} - \frac{1}{6}} \right) \cdot ( - 2,25)$

$d)\left[ {\left( {\frac{1}{4} - 0,5} \right) \cdot 2 + \frac{8}{3}} \right]:2.$ $d)\left[ {\left( {\frac{1}{4} - 0,5} \right) \cdot 2 + \frac{8}{3}} \right]:2.$

Gợi ý đáp án

$\begin{array}{l}0,3 - \frac{4}{9}:\frac{4}{3} \cdot \frac{6}{5} + 1\\ = \frac{3}{{10}} - \frac{4}{9}.\frac{3}{4}.\frac{6}{5} + 1\\ = \frac{3}{{10}} - \frac{2}{5} + 1\\ = \frac{3}{{10}} - \frac{4}{{10}} + \frac{{10}}{{10}}\\ = \frac{9}{{10}}\end{array}$ $\begin{array}{l}0,3 - \frac{4}{9}:\frac{4}{3} \cdot \frac{6}{5} + 1\\ = \frac{3}{{10}} - \frac{4}{9}.\frac{3}{4}.\frac{6}{5} + 1\\ = \frac{3}{{10}} - \frac{2}{5} + 1\\ = \frac{3}{{10}} - \frac{4}{{10}} + \frac{{10}}{{10}}\\ = \frac{9}{{10}}\end{array}$

$\begin{array}{l}{\left( {\frac{{ - 1}}{3}} \right)^2} - \frac{3}{8}:{(0,5)^3} - \frac{5}{2} \cdot ( - 4)\\ = \frac{1}{9} - \frac{3}{8}:\frac{1}{8} - \frac{5}{2}.\left( { - 4} \right)\\ = \frac{1}{9} - 3 + 10\\ = \frac{1}{9} - \frac{{27}}{9} + \frac{{90}}{9}\\ = \frac{{64}}{9}\end{array}$ $\begin{array}{l}{\left( {\frac{{ - 1}}{3}} \right)^2} - \frac{3}{8}:{(0,5)^3} - \frac{5}{2} \cdot ( - 4)\\ = \frac{1}{9} - \frac{3}{8}:\frac{1}{8} - \frac{5}{2}.\left( { - 4} \right)\\ = \frac{1}{9} - 3 + 10\\ = \frac{1}{9} - \frac{{27}}{9} + \frac{{90}}{9}\\ = \frac{{64}}{9}\end{array}$

$\begin{array}{l}1 + 2:\left( {\frac{2}{3} - \frac{1}{6}} \right) \cdot ( - 2,25)\\ = 1 + 2:\left( {\frac{4}{6} - \frac{1}{6}} \right) \cdot \left( { - \frac{9}{4}} \right)\\ = 1 + 2:\frac{1}{2}.\left( { - \frac{9}{4}} \right)\\ = 1 + 2.\frac{2}{1}.\left( { - \frac{9}{4}} \right)\\ = 1 + \left( { - 9} \right) = - 8\end{array}\begin{array}{l}1 + 2:\left( {\frac{2}{3} - \frac{1}{6}} \right) \cdot ( - 2,25)\\ = 1 + 2:\left( {\frac{4}{6} - \frac{1}{6}} \right) \cdot \left( { - \frac{9}{4}} \right)\\ = 1 + 2:\frac{1}{2}.\left( { - \frac{9}{4}} \right)\\ = 1 + 2.\frac{2}{1}.\left( { - \frac{9}{4}} \right)\\ = 1 + \left( { - 9} \right) = - 8\end{array}$ $\begin{array}{l}1 + 2:\left( {\frac{2}{3} - \frac{1}{6}} \right) \cdot ( - 2,25)\\ = 1 + 2:\left( {\frac{4}{6} - \frac{1}{6}} \right) \cdot \left( { - \frac{9}{4}} \right)\\ = 1 + 2:\frac{1}{2}.\left( { - \frac{9}{4}} \right)\\ = 1 + 2.\frac{2}{1}.\left( { - \frac{9}{4}} \right)\\ = 1 + \left( { - 9} \right) = - 8\end{array}\begin{array}{l}1 + 2:\left( {\frac{2}{3} - \frac{1}{6}} \right) \cdot ( - 2,25)\\ = 1 + 2:\left( {\frac{4}{6} - \frac{1}{6}} \right) \cdot \left( { - \frac{9}{4}} \right)\\ = 1 + 2:\frac{1}{2}.\left( { - \frac{9}{4}} \right)\\ = 1 + 2.\frac{2}{1}.\left( { - \frac{9}{4}} \right)\\ = 1 + \left( { - 9} \right) = - 8\end{array}$

$\begin{array}{l}\left[ {\left( {\frac{1}{4} - 0,5} \right) \cdot 2 + \frac{8}{3}} \right]:2\\ = \left[ {\left( {\frac{1}{4} - \frac{2}{4}} \right) \cdot 2 + \frac{8}{3}} \right].\frac{1}{2}\\ = \left( {\frac{{ - 1}}{4}.2 + \frac{8}{3}} \right).\frac{1}{2}\\ = \left( {\frac{{ - 1}}{2} + \frac{8}{3}} \right).\frac{1}{2}\\ = \frac{{13}}{6}.\frac{1}{2} = \frac{{13}}{{12}}\end{array}.$ $\begin{array}{l}\left[ {\left( {\frac{1}{4} - 0,5} \right) \cdot 2 + \frac{8}{3}} \right]:2\\ = \left[ {\left( {\frac{1}{4} - \frac{2}{4}} \right) \cdot 2 + \frac{8}{3}} \right].\frac{1}{2}\\ = \left( {\frac{{ - 1}}{4}.2 + \frac{8}{3}} \right).\frac{1}{2}\\ = \left( {\frac{{ - 1}}{2} + \frac{8}{3}} \right).\frac{1}{2}\\ = \frac{{13}}{6}.\frac{1}{2} = \frac{{13}}{{12}}\end{array}.$

Bài 5 trang 30 Toán 7 tập 1

Tìm x, biết:

$a) x + \left( { - \frac{2}{9}} \right) = \frac{{ - 7}}{{12}};$ $a) x + \left( { - \frac{2}{9}} \right) = \frac{{ - 7}}{{12}};$

$b) ( - 0,1) - x = \frac{{ - 7}}{6}$ $b) ( - 0,1) - x = \frac{{ - 7}}{6}$

$c) ( - 0,12) \cdot \left( {x - \frac{9}{{10}}} \right) = - 1,2;$ $c) ( - 0,12) \cdot \left( {x - \frac{9}{{10}}} \right) = - 1,2;$

$d) \left( {x - \frac{3}{5}} \right):\frac{{ - 1}}{3} = 0,4.$ $d) \left( {x - \frac{3}{5}} \right):\frac{{ - 1}}{3} = 0,4.$

Hướng dẫn giải

Quy tắc dấu ngoặc

+ Khi bỏ dấu ngoặc có dấu (+) đằng trước, ta giữ nguyên dầu của các số trong dấu ngoặc

a + (b + c) = a + b + c

a + (b – c) = a + b – c

+ Khi bỏ dấu ngoặc có dấu (-) đằng trước ta phải đổi dấu của các số hạng trong dấu ngoặc: Dấu (+) đổi thành dấu (-), dấu (-) đổi thành dấu (+)

a – (b + c) = a – b – c

a – (b – c) = a – b + c

Gợi ý đáp án

$\begin{array}{l}x + \left( { - \frac{2}{9}} \right) = \frac{{ - 7}}{{12}}\\x = \frac{{ - 7}}{{12}} + \frac{2}{9}\\x = \frac{{ - 21}}{{36}} + \frac{8}{{36}}\\x = \frac{{ - 13}}{{26}}\end{array}$ $\begin{array}{l}x + \left( { - \frac{2}{9}} \right) = \frac{{ - 7}}{{12}}\\x = \frac{{ - 7}}{{12}} + \frac{2}{9}\\x = \frac{{ - 21}}{{36}} + \frac{8}{{36}}\\x = \frac{{ - 13}}{{26}}\end{array}$

Vậy $x = \frac{{ - 13}}{{26}}.$ $x = \frac{{ - 13}}{{26}}.$

$\begin{array}{l}( - 0,1) - x = \frac{{ - 7}}{6}\\\frac{{ - 1}}{{10}} - x = \frac{{ - 7}}{6}\\x = \frac{{ - 1}}{{10}} + \frac{7}{6}\\x = \frac{{ - 3}}{{30}} + \frac{{35}}{{30}}\\x = \frac{{32}}{{30}}\\x = \frac{{16}}{{15}}\end{array}$ $\begin{array}{l}( - 0,1) - x = \frac{{ - 7}}{6}\\\frac{{ - 1}}{{10}} - x = \frac{{ - 7}}{6}\\x = \frac{{ - 1}}{{10}} + \frac{7}{6}\\x = \frac{{ - 3}}{{30}} + \frac{{35}}{{30}}\\x = \frac{{32}}{{30}}\\x = \frac{{16}}{{15}}\end{array}$

Vậy $x = \frac{{16}}{{15}}$ $x = \frac{{16}}{{15}}$

$\begin{array}{l}( - 0,12) \cdot \left( {x - \frac{9}{{10}}} \right) = - 1,2\\\frac{{ - 3}}{{25}} \cdot \left( {x - \frac{9}{{10}}} \right) = \frac{{ - 6}}{5}\\x - \frac{9}{{10}} = \frac{{ - 6}}{5}:\left( {\frac{{ - 3}}{{25}}} \right)\\x - \frac{9}{{10}} = \frac{{ - 6}}{5}.\frac{{ - 25}}{3}\\x - \frac{9}{{10}} = 10\\x = 10 + \frac{9}{{10}}\\x = \frac{{109}}{{10}}\end{array}$ $\begin{array}{l}( - 0,12) \cdot \left( {x - \frac{9}{{10}}} \right) = - 1,2\\\frac{{ - 3}}{{25}} \cdot \left( {x - \frac{9}{{10}}} \right) = \frac{{ - 6}}{5}\\x - \frac{9}{{10}} = \frac{{ - 6}}{5}:\left( {\frac{{ - 3}}{{25}}} \right)\\x - \frac{9}{{10}} = \frac{{ - 6}}{5}.\frac{{ - 25}}{3}\\x - \frac{9}{{10}} = 10\\x = 10 + \frac{9}{{10}}\\x = \frac{{109}}{{10}}\end{array}$

Vậy $x = \frac{{109}}{{10}}$ $x = \frac{{109}}{{10}}$.

$\begin{array}{l}\left( {x - \frac{3}{5}} \right):\frac{{ - 1}}{3} = 0,4\\\left( {x - \frac{3}{5}} \right):\frac{{ - 1}}{3} = \frac{2}{5}\\x - \frac{3}{5} = \frac{2}{5}.\frac{{ - 1}}{3}\\x - \frac{3}{5} = \frac{{ - 2}}{{15}}\\x = \frac{{ - 2}}{{15}} + \frac{3}{5}\\x = \frac{7}{{15}}\end{array}$ $\begin{array}{l}\left( {x - \frac{3}{5}} \right):\frac{{ - 1}}{3} = 0,4\\\left( {x - \frac{3}{5}} \right):\frac{{ - 1}}{3} = \frac{2}{5}\\x - \frac{3}{5} = \frac{2}{5}.\frac{{ - 1}}{3}\\x - \frac{3}{5} = \frac{{ - 2}}{{15}}\\x = \frac{{ - 2}}{{15}} + \frac{3}{5}\\x = \frac{7}{{15}}\end{array}$

Vậy $x = \frac{7}{{15}}.$ $x = \frac{7}{{15}}.$

Bài 6 trang 30 Toán 7 tập 1

Sắp xếp các số sau theo thứ tự tăng dần:

$a) {(0,2)^0};{(0,2)^3};{(0,2)^1};{(0,2)^2};$ $a) {(0,2)^0};{(0,2)^3};{(0,2)^1};{(0,2)^2};$

$b) {( - 1,1)^2};{( - 1,1)^0};{( - 1,1)^1};{( - 1,1)^3}.$ $b) {( - 1,1)^2};{( - 1,1)^0};{( - 1,1)^1};{( - 1,1)^3}.$

Hướng dẫn giải

Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ

a^m . aⁿ = a^{m + n}

Khi chia hai lũy thừa cùng cơ số (khác 0) ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia:

a^m : aⁿ = a^{m – n}

x⁰ = 1

Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ:

(x^m)ⁿ = x^{m . n}

Gợi ý đáp án

$a) {\left( {0,2} \right)^0} = 1;{\left( {0,2} \right)^1} = 0,2;{\left( {0,2} \right)^2} = 0,04;{\left( {0,2} \right)^3} = 0,008$ $a) {\left( {0,2} \right)^0} = 1;{\left( {0,2} \right)^1} = 0,2;{\left( {0,2} \right)^2} = 0,04;{\left( {0,2} \right)^3} = 0,008$

Vì 0,008 < 0, 04 < 0,2< 1 nên sắp xếp các số theo thứ tự tăng dần là:

${(0,2)^0};{(0,2)^1};{(0,2)^2};{(0,2)^3}.$ ${(0,2)^0};{(0,2)^1};{(0,2)^2};{(0,2)^3}.$

$b) {\left( { - 1,1} \right)^0} = 1;{\left( { - 1,1} \right)^1} = - 1,1;{\left( { - 1,1} \right)^2} = 1,21;{\left( { - 1,1} \right)^3} = - 1,331$ $b) {\left( { - 1,1} \right)^0} = 1;{\left( { - 1,1} \right)^1} = - 1,1;{\left( { - 1,1} \right)^2} = 1,21;{\left( { - 1,1} \right)^3} = - 1,331$

Vì -1,331 < -1,1 < 1 < 1,21 nên sắp xếp các số theo thứ tự tăng dần là:

${( - 1,1)^3};{( - 1,1)^1}{( - 1,1)^0};{( - 1,1)^2}$ ${( - 1,1)^3};{( - 1,1)^1}{( - 1,1)^0};{( - 1,1)^2}$

Bài 7 trang 30 Toán 7 tập 1

Trọng lượng của một vật thể trên Mặt Trăng bằng khoảng $\frac{1}{6}$ $\frac{1}{6}$ trọng lượng của nó trên Trái Đất. Biết trọng lượng của một vật trên Trái Đất được tính theo công thức: $P = 10\;{\rm{m}}$ $P = 10\;{\rm{m}}$ với P là trọng lượng của vật tính theo đơn vị Niu-tơn (kí hiệu ${\rm{N}})$ ${\rm{N}})$; m là khối lượng của vật tính theo đơn vị ki-lô-gam.

(Nguồn: Khoa học tự nhiên 6, NXB Đại học Sư phạm, 2021)

Nếu trên Trái Đất một nhà du hành vũ trụ có khối lượng là $75,5\;{\rm{kg}}$ $75,5\;{\rm{kg}}$ thì trọng lượng của người đó trên Mặt Trăng sẽ là bao nhiêu Niu-tơn (làm tròn kết quả đến hàng phần trăm)?

Gợi ý đáp án

Trọng lượng người đó trên Trái Đất là: 75,5.10 = 755 (N)

Trọng lượng người đó trên Mặt Trăng là:

$755.\dfrac{1}{6} \approx 125,83 (N)$ $755.\dfrac{1}{6} \approx 125,83 (N)$

Bài 8 trang 31 Toán 7 tập 1

Một người đi quãng đường từ địa điểm A đến địa điểm B với vận tốc $30\;{\rm{km}}/{\rm{h}}$ $30\;{\rm{km}}/{\rm{h}}$ mất 3,5 giờ. Từ địa điểm B quay trở về địa điểm A, người đó đi với vận tốc $36\;{\rm{km}}/{\rm{h}}$ $36\;{\rm{km}}/{\rm{h}}$. Tính thời gian đi từ địa điểm B quay trở về địa điểm A của người đó.

Hướng dẫn giải

Quãng đường bằng vận tốc nhân với thời gian.

Gợi ý đáp án

Quãng đường AB dài: 30.3,5 = 105 (km)

Thời gian người đó đi quãng đường từ địa điểm B về địa điểm A là:

$105:36 = \frac{{35}}{{12}} (giờ)$ $105:36 = \frac{{35}}{{12}} (giờ)$

Bài 9 trang 31 Toán 7 tập 1

Một trường trung học cơ sở có các lớp 7A, 7B, 7C, 7D, 7E; mỗi lớp đều có 40 học sinh. Sau khi sơ kết Học kì I, số học sinh ở mức Tốt của mỗi lớp đó được thể hiện qua biểu đồ cột ở Hình 5 .

a) Lớp nào có số học sinh ở mức Tốt ít hơn một phần tư số học sinh của cả lớp?

b) Lớp nào có số học sinh ở mức Tốt nhiều hơn một phần ba số học sinh của cả lớp?

c) Lớp nào có tỉ lệ học sinh ở mức Tốt cao nhất, thấp nhất?

Phương pháp giải

- Tính một phần ba và một phần tư số học sinh của cả lớp

- Quan sát biểu đồ và trả lời câu hỏi.

Gợi ý đáp án

a) Một phần tư số học sinh cả lớp là: $\frac{1}{4}.40 = 10$ $\frac{1}{4}.40 = 10$ (học sinh).

=>Lớp 7C và 7E có số học sinh ở mức Tốt ít hơn một phần tư số học sinh của cả lớp.

b) Một phần ba số học sinh cả lớp là: $\frac{1}{3}.40 \approx 13$ $\frac{1}{3}.40 \approx 13$ (học sinh).

=> Lớp 7A và 7D có số học sinh ở mức Tốt nhiều hơn một phần ba số học sinh của cả lớp.

c) Lớp 7D có tỉ lệ học sinh ở mức Tốt cao nhất.

Lớp 7E có tỉ lệ học sinh ở mức Tốt thấp nhất

Bài 10 trang 31 Toán 7 tập 1

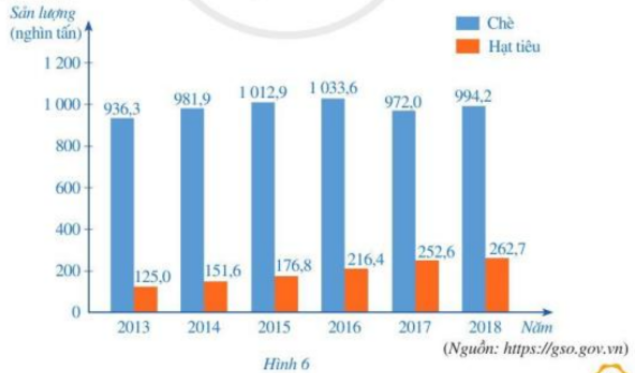
Sản lượng chè và hạt tiêu xuất khẩu của Việt Nam qua một số năm được biểu diễn trong biểu đồ cột kép ở Hình 6 .

a) Những năm nào sản lượng chè xuất khẩu trên 1 triệu tấn? Sản lượng hạt tiêu xuất khẩu trên 0,2 triệu tấn?

b) Năm nào Việt Nam có sản lượng chè xuất khẩu lớn nhất? Sản lượng hạt tiêu xuất khẩu lớn nhất?

c) Tính tỉ số phần trăm của sản lượng chè xuất khẩu năm 2013 và sản lượng chè xuất khẩu năm 2018.

Phương pháp giải

- Quan sát biểu đồ và trả lời câu hỏi.

- Tỉ số phần trăm của sản lượng chè xuất khẩu năm 2013 và sản lượng chè xuất khẩu năm 2018 = sản lượng chè xuất khẩu năm 2013 : sản lượng chè xuất khẩu năm 2018.100%

Gợi ý đáp án

a) Năm 2015 và năm 2016 sản lượng chè xuất khẩu trên 1 triệu tấn.

Năm 2016, 2017, 2018 sản lượng hạt tiêu xuất khẩu trên 0,2 triệu tấn.

b) Năm 2016 Việt Nam có sản lượng chè xuất khẩu lớn nhất.

Năm 2018 Việt Nam sản lượng hạt tiêu xuất khẩu lớn nhất.

c) Tỉ số phần trăm của sản lượng chè xuất khẩu năm 2013 và sản lượng chè xuất khẩu năm 2018 là:

$\frac{{936,3}}{{994,2}}.100\% = 94,18\%$ $\frac{{936,3}}{{994,2}}.100\% = 94,18\%$

Chia sẻ bởi: