Toán 7 Bài 3: Hai tam giác bằng nhau Giải Toán lớp 7 trang 78, 79 - Tập 2 sách Cánh diều

Giải Toán 7 Bài 3: Hai tam giác bằng nhau Cánh diều là tài liệu vô cùng hữu ích giúp các em học sinh lớp 7 có thêm nhiều gợi ý tham khảo để giải các bài tập từ 1→7 trang 78, 79 tập 2.

Giải bài tập Toán 7 Cánh diều tập 2 trang 78, 79 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài, đồng thời là tư liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy sau đây là nội dung chi tiết Giải Toán 7 Bài 3 trang 78, 79 Cánh diều, mời các bạn cùng theo dõi.

Giải Toán 7 trang 78, 79 Cánh diều

Bài 1

Cho biết ∆ABC = ∆DEG, AB = 3 cm, BC = 4 cm, CA = 6 cm. Tìm độ dài các cạnh của tam giác DEG.

Gợi ý đáp án

Do ∆ABC = ∆DEG nên AB = DE (2 cạnh tương ứng), BC = EG (2 cạnh tương ứng), CA = GD (2 cạnh tương ứng).

Do đó DE = 3 cm, EG = 4 cm, GD = 6 cm.

Bài 2

Cho biết \(\Delta PQR = \Delta IHK,\widehat P = 71^\circ ,\widehat Q = 49^\circ\) . Tính số đo góc K của tam giác IHK.

Gợi ý đáp án

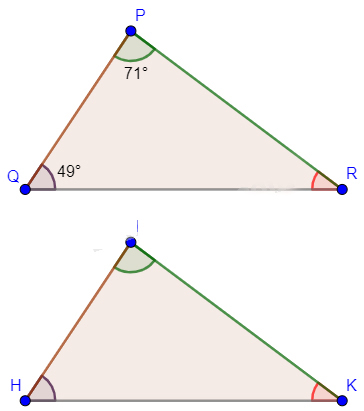
Ta có: \(\Delta PQR = \Delta IHK\) nên \(\widehat P = \widehat I;\widehat Q = \widehat H;\widehat R = \widehat K.\)

\(\Rightarrow \widehat I = 71^\circ ,\widehat H = 49^\circ\). Mà tổng 3 góc trong một tam giác bằng 180° nên trong tam giác \(IHK: \widehat I + \widehat H + \widehat K = 180^\circ\)

Vậy \(\widehat K = 180^\circ - 71^\circ - 49^\circ = 60^\circ\).

Bài 3

Cho \(\Delta ABC = \Delta MNP\) và \(\widehat A + \widehat N = 125^\circ\). Tính số đo góc P.

Tổng ba góc trong một tam giác bằng 180°.

Gợi ý đáp án

Ta có: \(\Delta ABC = \Delta MNP\) nên \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P.\)

Mà \(\widehat A + \widehat N = 125^\circ\) hay \(\widehat M + \widehat N = 125^\circ\). Tổng ba góc trong một tam giác bằng 180°.

Trong tam giác MNP:

\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\125^\circ + \widehat P = 180^\circ \\ \to \widehat P = 180^\circ - 125^\circ = 55^\circ \end{array}\)

Vậy số đo góc P là 55°.

Bài 4

Cho tam giác ABC và điểm M thuộc cạnh BC thỏa mãn \(\Delta AMB = \Delta AMC\)(Hình 32). Chứng minh rằng:

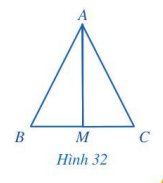
a) M là trung điểm của đoạn thẳng BC.

b) Tia AM là tia phân giác của góc BAC và \(AM \bot BC\).

Gợi ý đáp án

a) Ta có:\(\Delta AMB = \Delta AMC\) nên AB = AC, MB = MC nên M là trung điểm của đoạn thẳng BC.

b) Ta có: \(\Delta AMB = \Delta AMC\)nên \(\widehat {AMB} = \widehat {AMC},\widehat {MAB} = \widehat {MAC},\widehat {MBA} = \widehat {MCA}.\)

Vậy tia AM là tia phân giác của góc BAC vì \(\widehat {MAB} = \widehat {MAC}.\)

Ta thấy: \(\widehat {AMB} = \widehat {AMC}\)mà ba điểm B, M, C thẳng hàng nên \(\widehat {BMC} = 180^\circ .\)

\(\Rightarrow \widehat {AMB} = \widehat {AMC} = \dfrac{1}{2}.\widehat {BMC} = \dfrac{1}{2}.180^\circ = 90^\circ\). Vậy \(AM \bot BC.\)