Toán 7 Bài tập cuối chương IV - Cánh diều Giải Toán lớp 7 trang 108 - Tập 1

Bài trước

Mục lục

Bài sau

Bài tập cuối chương IV lớp 7 Cánh diều giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời 10 câu hỏi trong SGK trang 108 được nhanh chóng và thuận tiện hơn.

Bài tập cuối chương 4 Toán 7 Cánh diều được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 7 tập 1. Giải Toán 7 Bài tập cuối chương 4 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.

Toán 7 Bài tập cuối chương IV - Cánh diều

Giải Toán 7 trang 108 Cánh diều - Tập 1

Bài 1

a) Cho một ví dụ về hai góc kề nhau, hai góc kề bù, hai góc đối đỉnh.

b) Thế nào là tia phân giác của một góc?

c) Cho một ví dụ về hai góc đồng vị, hai góc so le trong.

d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị có bằng nhau không? Hai góc so le trong có bằng nhau hay không?

e) Phát biểu tiên đề Euclid về đường thẳng song song.

Gợi ý đáp án

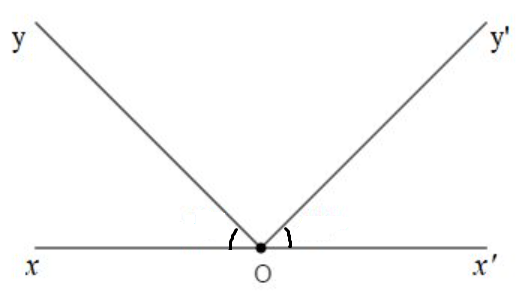
a) Ví dụ: Hai góc aOb và bOc là hai góc kề nhau (như hình vẽ).

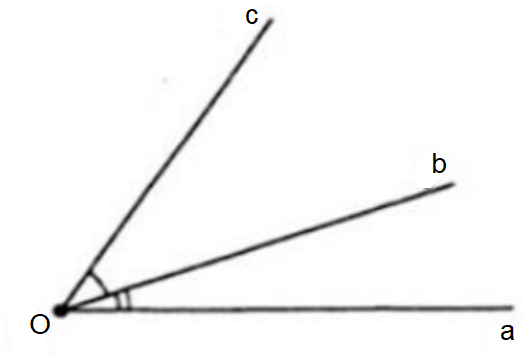
Ví dụ: Hai góc xOy và yOz là hai góc kề bù (như hình vẽ).

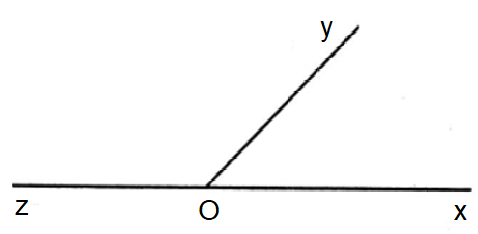
Ví dụ: Hai góc O₁ và O₂ là hai góc đối đỉnh.

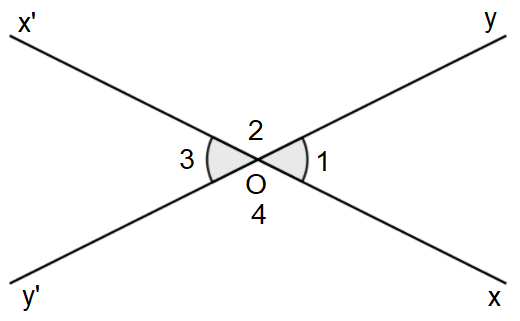
b) Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.

c) Ví dụ: Hai góc M₁ và N₁ là hai góc đồng vị.

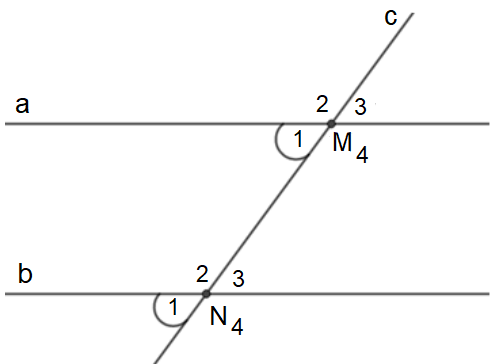
Ví dụ: Hai góc A₁ và B₁ là hai góc so le trong.

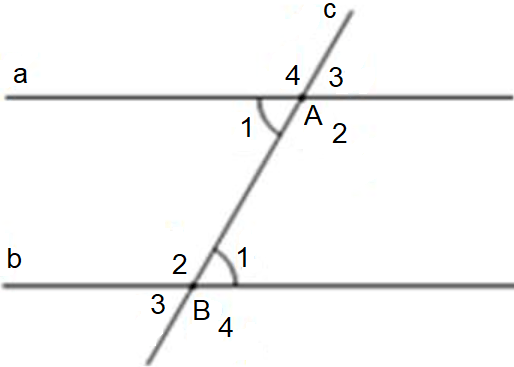
d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau và hai góc so le trong bằng nhau.

e) Tiên đề Euclid về đường thẳng song song:

Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

Bài 2

a) Hai góc có tổng số đo bằng 180 ^\circ có phải là hai góc kề bù hay không?

b) Hai góc bằng nhau và có chung đỉnh có phải là hai góc đối đỉnh hay không?

Gợi ý đáp án

a) Hai góc có tổng số đo bằng $180 ^\circ$ $180 ^\circ$ không phải là hai góc kề bù, vì 2 góc kề bù phải là 2 góc kề nhau và có tổng số đo bằng $180 ^\circ$ $180 ^\circ$, chẳng hạn:

Góc xOy và góc xOz có tổng số đo bằng 180^\circ nhưng không phải là hai góc kề bù, vì không kề nhau

b) Hai góc bằng nhau và có chung đỉnh không phải là hai góc đối đỉnh, chẳng hạn:

Góc mAq và nAp bằng nhau và có chung đỉnh nhưng không phải là hai góc đối đỉnh.

Bài 3

Tìm cặp đường thẳng song song trong mỗi hình 53a, 53b, 53c, 53d và giải thích vì sao.

Gợi ý đáp án

a) Vì $\widehat {{A_1}} = \widehat {{B_1}}( = 124^\circ$ $\widehat {{A_1}} = \widehat {{B_1}}( = 124^\circ$). Mà 2 góc này ở vị trí so le trong nên z // t

b) Vì $\widehat {{D_1}} + \widehat {{D_2}} = 180^\circ$ $\widehat {{D_1}} + \widehat {{D_2}} = 180^\circ$( 2 góc kề bù) nên $90^\circ + \widehat {{D_2}} = 180^\circ \Rightarrow \widehat {{D_2}} = 180^\circ - 90^\circ = 90^\circ$ $90^\circ + \widehat {{D_2}} = 180^\circ \Rightarrow \widehat {{D_2}} = 180^\circ - 90^\circ = 90^\circ$

Vì $\widehat {{D_2}} = \widehat {{C_1}}( = 90^\circ )$ $\widehat {{D_2}} = \widehat {{C_1}}( = 90^\circ )$. Mà 2 góc này ở vị trí so le trong nên m // n

c) Vì $\widehat {{E_1}} + \widehat {{E_2}} = 180^\circ$ $\widehat {{E_1}} + \widehat {{E_2}} = 180^\circ$( 2 góc kề bù) nên $110^\circ + \widehat {{E_2}} = 180^\circ \Rightarrow \widehat {{E_2}} = 180^\circ - 110^\circ = 70^\circ$ $110^\circ + \widehat {{E_2}} = 180^\circ \Rightarrow \widehat {{E_2}} = 180^\circ - 110^\circ = 70^\circ$

Vì $\widehat {{E_2}} = \widehat {{G_1}}( = 70^\circ )$ $\widehat {{E_2}} = \widehat {{G_1}}( = 70^\circ )$. Mà 2 góc này ở vị trí so le trong nên x //y

d) Vì $\widehat {{K_1}} + \widehat {{K_2}} = 180^\circ$ $\widehat {{K_1}} + \widehat {{K_2}} = 180^\circ$( 2 góc kề bù) nên $\widehat {{K_1}} + 56^\circ = 180^\circ \Rightarrow \widehat {{K_1}} = 180^\circ - 56^\circ = 124^\circ$ $\widehat {{K_1}} + 56^\circ = 180^\circ \Rightarrow \widehat {{K_1}} = 180^\circ - 56^\circ = 124^\circ$

Vì $\widehat {{H_1}} = \widehat {{K_1}}( = 124^\circ )$ $\widehat {{H_1}} = \widehat {{K_1}}( = 124^\circ )$. Mà 2 góc này ở vị trí so le trong nên x //y

Bài 4

Quan sát Hình 54, trong đó Cx song song với AB.

a) Chứng minh rằng Cx song song với DE.

b) Chứng minh rằng $\widehat {BCx} = 45^\circ$ $\widehat {BCx} = 45^\circ$và $\widehat {DCx} = 60^\circ$ $\widehat {DCx} = 60^\circ$

c) Tính $\widehat {BCD}$ $\widehat {BCD}$

Gợi ý đáp án

a) Vì AE \bot AB; AE \bot ED nên AB // ED (2 đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)

Mà Cx // AB (gt)

\Rightarrow Cx // ED (2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau)

b) Vì Cx // AB nên $\widehat {ABC} = \widehat {BCx}$ $\widehat {ABC} = \widehat {BCx}$ ( 2 góc so le trong), mà $\widehat {ABC} = 45^\circ \Rightarrow \widehat {BCx} = 45^\circ$ $\widehat {ABC} = 45^\circ \Rightarrow \widehat {BCx} = 45^\circ$

Vì Cx // ED nên $\widehat {EDC} = \widehat {DCx}$ $\widehat {EDC} = \widehat {DCx}$ ( 2 góc so le trong), mà $\widehat {EDC} = 60^\circ \Rightarrow \widehat {DCx} = 60^\circ$ $\widehat {EDC} = 60^\circ \Rightarrow \widehat {DCx} = 60^\circ$

c) Vì tia Ox nằm trong góc BCD nên $\widehat {BCD} = \widehat {BCx} + \widehat {DCx} = 45^\circ + 60^\circ = 105^\circ$ $\widehat {BCD} = \widehat {BCx} + \widehat {DCx} = 45^\circ + 60^\circ = 105^\circ$

Bài 5

Quan sát Hình 55, trong đó mq // xt

a) Kể tên các cặp góc đồng vị bằng nhau.

b) Tìm số đo các góc BAC, CDE.

c) Bạn Nam cho rằng: Qua điểm C kẻ một đường thẳng c song song với hai đường thẳng mq và xt thì sẽ tính được $\widehat {BCE} = 82^\circ .$ $\widehat {BCE} = 82^\circ .$ Theo em, bạn Nam nói đúng hay sai? Vì sao?

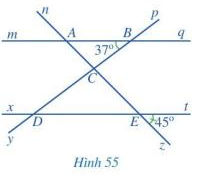
Gợi ý đáp án

a) Các cặp góc đồng vị bằng nhau là: góc mAn và xEn; góc mAz và xEz; góc nAq và nEt; góc qAz và tEz; góc pBq và pDt; góc qBy và tDy; góc mBy và xDy; góc pBm và pDx

b) Vì $\widehat {CED} = \widehat {zEt}$ $\widehat {CED} = \widehat {zEt}$( 2 góc đối đỉnh) nên $\widehat {CED} = 45^\circ$ $\widehat {CED} = 45^\circ$

Mà mq // xt nên $\widehat {BAC} = \widehat {CED}$ $\widehat {BAC} = \widehat {CED}$ ( 2 góc so le trong)

$\Rightarrow \widehat {BAC} = 45^\circ$ $\Rightarrow \widehat {BAC} = 45^\circ$

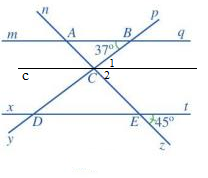
Bạn Nam nói đúng vì:

Vì c // mq nên $\widehat {ABC} = \widehat {{C_1}}$ $\widehat {ABC} = \widehat {{C_1}}$ ( 2 góc so le trong) nên $\widehat {{C_1}} = 37^\circ$ $\widehat {{C_1}} = 37^\circ$

Vì c // xt nên $\widehat {CED} = \widehat {{C_2}}$ $\widehat {CED} = \widehat {{C_2}}$ ( 2 góc so le trong) nên $\widehat {{C_2}} = 45^\circ$ $\widehat {{C_2}} = 45^\circ$

Vì $\widehat {{C_1}} + \widehat {{C_2}} = \widehat {BCE}$ $\widehat {{C_1}} + \widehat {{C_2}} = \widehat {BCE}$ nên $\widehat {BCE} = \widehat {{C_1}} + \widehat {{C_2}} = 37^\circ + 45^\circ = 82^\circ$ $\widehat {BCE} = \widehat {{C_1}} + \widehat {{C_2}} = 37^\circ + 45^\circ = 82^\circ$