Toán 7 Bài 1: Tập hợp Q các số hữu tỉ Giải Toán lớp 7 trang 10 - Tập 1 sách Cánh diều

Giải Toán lớp 7 trang 10, 11 tập 1 Cánh diều giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần Luyện tập vận dụng và 10 bài tập thuộc bài 1 Tập hợp Q các số hữu tỉ được nhanh chóng và dễ dàng hơn.

Toán 7 Cánh diều tập 1 trang 10, 11 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 7. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 7 Tập hợp Q các số hữu tỉ trang 10, 11 Cánh diều mời các bạn cùng theo dõi.

Phần Luyện tập và Vận dụng

Phần Bài tập

Bài 1 trang 10 Toán 7 tập 1

Các số 13, -29; -2,1; 2,28;\(\frac{{ - 12}}{{ - 18}}\) có là số hữu tỉ không? Vì sao?

Gợi ý đáp án

Các số \(13, -29; -2,1; 2,28; \frac{{ - 12}}{{ - 18}}\) có là số hữu tỉ vì:

\(13 = \frac{{13}}{1}; - 29 = \frac{{ - 29}}{1}; - 2,1 = \frac{{21}}{{10}};2,28 = \frac{{228}}{{100}} = \frac{{54}}{{25}};\frac{{ - 12}}{{ - 18}} = \frac{2}{3}\)

Chú ý: Một số nguyên cũng là một số hữu tỉ.

Bài 2 trang 10 Toán 7 tập 1

Gợi ý đáp án

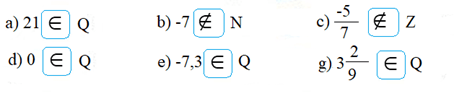
Bài 3 trang 10 Toán 7 tập 1

Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

Gợi ý đáp án 

a) Mọi số tự nhiên m bất kỳ đều biểu diễn được dưới dạng phân số \(\frac{m}{1}\)

=> Nếu m là số tự nhiên thì m cũng là số hữu tỉ.

=> Phát biểu a đúng.

b) Mọi số nguyên m bất kỳ đều biểu diễn được dưới dạng phân số \(\frac{m}{1}\)

=> Nếu m là số nguyên thì m cũng là số hữu tỉ.

=> Phát biểu b đúng

c) Nếu m là số hữu tỉ thì m có thể là số tự nhiên.

Ví dụ: -3 vừa là số hữu tỉ vừa là số tự nhiên.

Nếu m là số hữu tỉ thì m có thể không phải là số tự nhiên.

Ví dụ: \(\frac{5}{6}\) là số hữu tỉ nhưng không phải là số tự nhiên.

=> Nếu m là số hữu tỉ thì m chưa chắc là số tự nhiên.

=> Phát biểu c sai.

d) Nếu m là số hữu tỉ thì m có thể là số nguyên.

Ví dụ: −2 vừa là số hữu tỉ vừa là số nguyên.

Nếu m là số hữu tỉ thì m có thể không phải là số nguyên.

Ví dụ: \(\frac{1}{3}\) là số hữu tỉ nhưng không phải là số nguyên.

=> Nếu m là số hữu tỉ thì m chưa chắc là số nguyên.

=> Phát biểu d sai

e) Mọi số tự nhiên m bất kỳ đều biểu diễn được dưới dạng phân số \(\frac{m}{1}\)

=> Nếu m là số tự nhiên thì m cũng là số hữu tỉ.

=> Phát biểu e sai.

g) Mọi số nguyên m bất kỳ đều biểu diễn được dưới dạng phân số \(\frac{m}{1}\)

=> Nếu m là số nguyên thì m cũng là số hữu tỉ.

=> Phát biểu g sai.

Bài 4 trang 11 Toán 7 tập 1

Quan sát trục số sau và cho biết điểm A, B, C, D biểu diễn những số nào:

Gợi ý đáp án

- Đoạn thẳng đơn vị chia thành 7 đoạn thẳng bằng nhau, đơn vị mới bằng \(\frac{1}{7}\) đơn vị cũ.

Quan sát phần hình vẽ phía bên phải điểm O:

+ Điểm C nằm cách O một đoạn bằng 2 đơn vị mới.

=> Điểm C biểu diễn số hữu tỉ: \(\frac{2}{7}\)

+ Điểm D nằm cách O một đoạn bằng 6 đơn vị mới

=> Điểm D biểu diễn số hữu tỉ: \(\frac{6}{7}\)

Quan sát phần hình vẽ phía bên trái điểm O (các số hữu tỉ là các số âm)

+ Điểm B nằm cách O một đoạn bằng 3 đơn vị mới.

=> Điểm B biểu diễn số hữu tỉ: \(- \frac{3}{7}\)

+ Điểm A nằm cách O một đoạn bằng 9 đơn vị mới

=> Điểm A biểu diễn số hữu tỉ: \(- \frac{9}{7}\)

Bài 5 trang 11 Toán 7 tập 1

Tìm số đối của mỗi số sau:

\(\frac{9}{{25}};{\text{ }}\frac{{ - 8}}{7};{\text{ }} - \frac{{15}}{{31}};{\text{ }}\frac{5}{{ - 6}};{\text{ }}3,9;{\text{ - }}12,5\)

Gợi ý đáp án

- Số đối của số hữu tỉ \(\frac{9}{{25}}\) là số \(- \frac{9}{{25}}\)

- Số đối của số hữu tỉ \(\frac{{ - 8}}{7}\) là số \(\frac{{ 8}}{7}\)

- Số đối của số hữu tỉ \(- \frac{{15}}{{31}}\) là số \(\frac{{15}}{{31}}\)

- Số đối của số hữu tỉ \(\frac{5}{{ - 6}}\) là số \(\frac{5}{{ 6}}\)

- Số đối của số hữu tỉ 3,9 là số -3,9

- Số đối của số hữu tỉ -12,5 là số 12,5

Bài 6 trang 11 Toán 7 tập 1

Biểu diễn số đối của mỗi số đã cho trên trục số sau:

Gợi ý đáp án

- Số đối của số hữu tỉ \(-\frac{5}{6}\) là số \(\frac{5}{6}\)

- Số đối của số hữu tỉ \(- \frac{1}{3}\) là số \(\frac{1}{3}\)

- Số đối của số hữu tỉ \(\frac{7}{6}\) là số \(-\frac{7}{6}\)

Biểu diễn các số trên trục số như sau:

Bài 7 trang 11 Toán 7 tập 1

So sánh:

Gợi ý đáp án

a) 2,4 và \(2\frac{3}{5}\)

Ta có:

\(\begin{matrix} 2.4 = \dfrac{{24}}{{10}} = \dfrac{{12}}{5} \hfill \\ 2\dfrac{3}{5} = \dfrac{{13}}{5} \hfill \\ \end{matrix}\)

Do 12 < 13 => \(\frac{{12}}{5} < \frac{{13}}{5}\)

=> \(2.4 < 2\frac{3}{5}\)

Vậy \(2.4 < 2\frac{3}{5}\)

b) -0,12 và \(- \frac{2}{5}\)

Ta có:

\(\begin{matrix} - 0,12 = - \dfrac{{12}}{{100}} = - \dfrac{3}{{25}} \hfill \\ - \dfrac{2}{5} = \dfrac{{ - 2.5}}{{5.5}} = - \dfrac{{10}}{{25}} \hfill \\ \end{matrix}\)

Do 3 < 10 => -3 > -10

=> \(- \frac{3}{{25}} > - \frac{{10}}{{25}}\)

=> \(- 0,12 > - \frac{2}{5}\)

Vậy \(- 0,12 > - \frac{2}{5}\)

c) \(- \frac{2}{7}\) và -0,3

Ta có: \(- 0,3 = \frac{{ - 3}}{{10}}\)

\(\begin{matrix} \dfrac{{ - 3}}{{10}} = \dfrac{{ - 3.7}}{{7.10}} = - \dfrac{{21}}{{70}} \hfill \\ - \dfrac{2}{7} = \dfrac{{ - 2.10}}{{7.10}} = - \dfrac{{20}}{{70}} \hfill \\ \end{matrix}\)

Do 21 > 20 => -21 < -20

=> \(- \frac{{21}}{{70}} < - \frac{{20}}{{70}}\)

=> \(- 0,3 < - \frac{2}{7}\)

Vậy \(- 0,3 < - \frac{2}{7}\)

Bài 8 trang 11 Toán 7 tập 1

a) Sắp xếp các số sau theo thứ tự tăng dần \(- \frac{3}{7};0,4; - 0,5;\frac{2}{7}\).

b) Sắp xếp các số sau theo thứ tự giảm dần \(\frac{{ - 5}}{6}; - 0,75; - 4,5; - 1\).

Gợi ý đáp án

a) Ta có: \(0,4 = \frac{4}{{10}} = \frac{2}{5}, - 0,5 = - \frac{1}{2}\)

\(\begin{matrix} - \dfrac{3}{7} = \dfrac{{ - 30}}{{70}} \hfill \\ \dfrac{2}{5} = \dfrac{{2.14}}{{5.14}} = \dfrac{{28}}{{70}} \hfill \\ - \dfrac{1}{2} = \dfrac{{ - 1.35}}{{2.35}} = \dfrac{{ - 35}}{{70}} \hfill \\ \dfrac{2}{7} = \dfrac{{2.10}}{{7.10}} = \dfrac{{20}}{{70}} \hfill \\ \end{matrix}\)

Mà -35 < -30 < 30 < 28

Suy ra \(\frac{{ - 35}}{{70}} < \frac{{ - 30}}{{70}} < \frac{{20}}{{70}} < \frac{{28}}{{70}}\)

Suy ra \(- 0,5 < - \frac{3}{7} < \frac{2}{7} < 0,4\)

Vậy sắp xếp các số sau theo thứ tự tăng dần \(- 0,5; - \frac{3}{7};\frac{2}{7};0,4\)

b) Ta có: \(- 0,75 = - \frac{{75}}{{100}} = \frac{{ - 3}}{4}; - 4,5 = - \frac{{45}}{{10}} = \frac{{ - 9}}{2}\)

\(\begin{matrix} \dfrac{{ - 5}}{6} = \dfrac{{ - 5.2}}{{6.2}} = \dfrac{{ - 10}}{{12}} \hfill \\ \dfrac{{ - 3}}{4} = \dfrac{{ - 3.3}}{{4.3}} = \dfrac{{ - 9}}{{12}} \hfill \\ \dfrac{{ - 9}}{2} = \dfrac{{ - 9.6}}{{2.6}} = \dfrac{{ - 54}}{{12}} \hfill \\ - 1 = \dfrac{{ - 1.12}}{{1.12}} = \dfrac{{ - 12}}{{12}} \hfill \\ \end{matrix}\)

Mà -9 > -12 > -10 > -54

Suy ra \(\frac{{ - 9}}{{12}} > \frac{{ - 10}}{{12}} > \frac{{ - 12}}{{12}} > \frac{{ - 54}}{{12}}\)

Suy ra: \(- 0,75 > - \frac{5}{6} > - 1 > - 4,5\)

Vậy sắp xếp các số sau theo thứ tự giảm dần là: \(- 0,75; - \frac{5}{6}; - 1; - 4,5\)

Bài 9 trang 11 Toán 7 tập 1

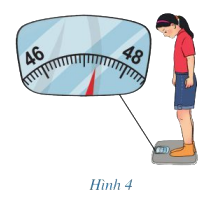
Bạn Linh đang cân khối lượng của mình (Hình 4) ở đó các vạch ghi 46 và 48 lấn lượt ứng với các số đo 46kg và 48kg, Khi nhìn vị trí mà chiếc kim chỉ vào, bạn minh đọc số đo là 47,15kg, bạn Dương đọc số đo là 47,3kg, bạn Quân đọc số đo là 47,65kg. Bạn nào đã đọc đúng số đo? Vì sao?

Gợi ý đáp án

Quan sát hình vẽ ta thấy:

Khoảng cách từ 46 đến 48 được chia thành 20 phần bằng nhau.

Mỗi vạch ứng với 2 : 20 = 0,1(g)

Vạch đậm chính giữa 46 và 48 là 47kg

Trên hình vẽ kim cân chỉ vào vạch số 3 tính từ vạch đậm chính giữa

Số cân nặng kim cân chỉ vào là

47 + 0,1 . 3 = 47,3 (kg)

Vậy bạn Dương là người đọc đúng số cân nặng của Linh.

Bài 10 trang 11 Toán 7 tập 1

Cô Hạnh dự định xây tầng hầm cho ngôi nhà của gia đình. Một công ty tư vấn xây dựng đã cung cấp cho cô Hạnh lựa chọn một trong sáu số đo chiều cao của tầng hầm như sau: 2,3 m; 2,35 m; 2,4 m; 2,55 m; 2,5 m; 2,75 m. Cô Hạnh dự định chọn chiều cao của tầng hầm lớn hơn \(\frac{{13}}{5}\)m để đảm bảo ánh sáng, thoáng đãng, cân đối về kiến trúc và thuận tiện trong sử dụng. Em hãy giúp cô Hạnh chọn đúng số đo chiều cao của tầng hầm.

Gợi ý đáp án

Ta có:

\(\begin{matrix} \dfrac{{13}}{5} = \dfrac{{13.20}}{{5.20}} = \dfrac{{260}}{{100}} \hfill \\ 2,3 = \dfrac{{23}}{{10}} = \dfrac{{230}}{{100}} \hfill \\ 2,35 = \dfrac{{235}}{{100}} \hfill \\ 2,4 = \dfrac{{24}}{{10}} = \dfrac{{240}}{{100}} \hfill \\ 2,55 = \dfrac{{255}}{{100}} \hfill \\ 2,5 = \dfrac{{25}}{{10}} = \dfrac{{250}}{{100}} \hfill \\ 2,75 = \dfrac{{275}}{{100}} \hfill \\ \end{matrix}\)

Ta có: 230 < 235 < 240 < 250 < 255 < 260 < 275

Suy ra \(\dfrac{{230}}{{100}} < \frac{{235}}{{100}} < \frac{{240}}{{100}} < \frac{{250}}{{100}} < \frac{{255}}{{100}} < \frac{{260}}{{100}} < \frac{{275}}{{100}}\)

=> \(2,3 < 2,35 < 2,4 < 2,5 < 2,55 < \frac{{13}}{5} < 2,75\)

Mà cô Hạnh dự định chọn chiều cao của tầng hầm lớn hơn \(\frac{{13}}{5}\)m

Lý thuyết Tập hợp Q các số hữu tỉ

1. Số hữu tỉ

Số hữu tỉ là số có thể viết dưới dạng \(\dfrac{a}{b}\) với \(a, b ∈ \mathbb Z, b \ne 0\) và tập hợp các số hữu tỉ được kí hiệu là \(\mathbb Q\)

Ví dụ: Các số \(5;\dfrac{{ - 1}}{2};\dfrac{2}{3}\);... là các số hữu tỉ

2. Biểu diễn số hữu tỉ trên trục số

Để biểu diễn số hữu tỉ a/b (a,b ∈ Z; b > 0) trên trục số ta làm như sau:

• Chia đoạn đơn vị [0;1] trên trục số thành b phần bằng nhau, mỗi phần là 1/b được gọi là đơn vị mới .

• Nếu a > 0 thì phân số a/b được biểu diễn bằng một điểm nằm bên phải điểm O và cách điểm O một đoạn bằng a lần đơn vị mới .

• Nếu a < 0 thì phân số a/b được biểu diễn bằng một điểm nằm bên trái điểm O và cách điểm O một đoạn bằng |a| lần đơn vị mới .

Mỗi số hữu tỉ được biểu diễn bởi một điểm trên trục số và không phụ thuộc vào cách chọn phân số xác định nó.

Ví dụ: Số hữu tỉ \(\dfrac{2}3\) được biểu diễn bởi điểm M trên trục số sau:

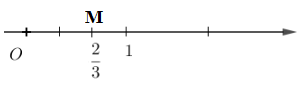
3. So sánh số hữu tỉ

Để so sánh hai số hữu tỉ x,y ta làm như sau:

- Viết x,y dưới dạng phân số cùng mẫu dương.

\(x = \dfrac{a}{m} ; y = \dfrac{b}{m} ( m>0)\)

- So sánh các tử là số nguyên a và b

Nếu a> b thì x > y

Nếu a = b thì x=y

Nếu a < b thì x < y.

Ví dụ: So sánh hai số \(x = \frac{2}{{ - 5}} và y = \frac{{ - 3}}{{13}}\)

Ta có \(x = \frac{2}{{ - 5}} = \frac{{2.\left( { - 13} \right)}}{{\left( { - 5} \right).\left( { - 13} \right)}} = \frac{{ - 26}}{{65}} và y = \frac{{ - 3}}{{13}} = \frac{{ - 3.5}}{{13.5}} = \frac{{ - 15}}{{65}}\)

Mà \(- 26 < - 15 \Rightarrow \frac{{ - 26}}{{65}} < \frac{{ - 15}}{{65}} hay x < y\)