Giải Toán lớp 7 trang 94, 95 tập 1 Cánh diều giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần Luyện tập vận dụng và 4 bài tập cuối bài Góc ở vị trí đặc biệt được chính xác thuận tiện hơn.

Toán 7 Cánh diều tập 1 trang 94, 95 hướng dẫn các em giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 7. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được. Vậy sau đây là trọn bộ tài liệu giải Toán 7 trang 94, 95 Cánh diều tập 1 mời các bạn cùng theo dõi.

Phần Luyện tập vận dụng

Luyện tập 1 trang 91 Toán 7 tập 1

Ở Hình 6, hai góc xOy và mOn có phải là hai góc kề nhau hay không? Vì sao?

Gợi ý đáp án

Ta có: Hai góc xOy và mOn có đỉnh O chung nhưng không có cạnh chung.

=> Hai góc xOy và mOn không là hai góc kề nhau.

Luyện tập 2 trang 92 Toán 7 tập 1

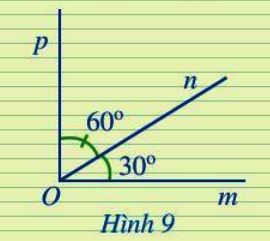
 Ở Hình 9, hai góc mOn và pOn có là hai góc kề nhau hay không? Tính số đo của góc mOp. 

Gợi ý đáp án

Ta có:

Hai góc mOn và pOn có chung đỉnh O, chung tia On. Đồng thời hai tia Op, Om nằm về hai phía so với tia On.

=> Hai góc mOn và pOn là hai góc kề nhau.

Ta có:

\(\begin{matrix} \widehat {mOp} = \widehat {mOn} + \widehat {nOm} \hfill \\ \Rightarrow \widehat {mOp} = {60^0} + {30^0} = {90^0} \hfill \\ \end{matrix}\)

Vậy \(\widehat {mOp} = {90^0}\)

Luyện tập 3 trang 93 Toán 7 tập 1

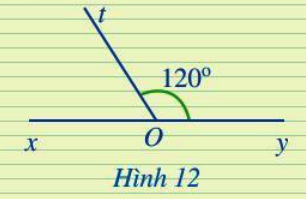
Tính góc xOt trong Hình 12.

Gợi ý đáp án

Hai góc xOt và yOt có chung đỉnh O, chung cạnh Ot và hai cạnh Ox và Oy nằm về hai phía của tia Ot.

=> Hai góc xOt và yOt kề nhau.

=> \(\widehat {xOy} = \widehat {xOt} + \widehat {yOt} = {180^0}\)

=> \(\widehat {xOt} = {180^0} - \widehat {yOt} = {180^0} - {120^0} = {60^0}\)

Vậy \(\widehat {xOt} = {60^0}\)

Luyện tập 4 trang 94 Toán 7 tập 1

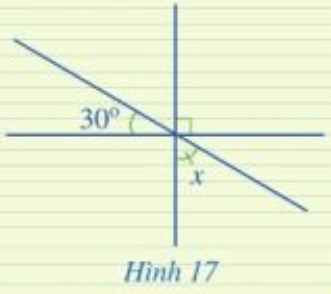
Tìm số đo x trong Hình 17.

Gợi ý đáp án 

Kí hiệu hình vẽ như sau:

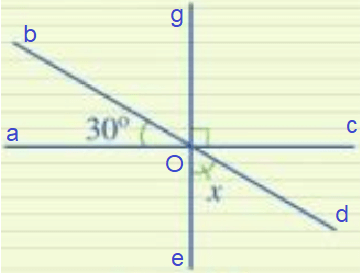
Ta có hai góc yOz’ và góc z’Om là hai góc kề nhau

Mà \(\widehat {yOm} = {90^0}\)

=> \(\widehat {yOz'} + \widehat {z'Om} = {180^0}\)

=> \(\widehat {z'Om} = {180^0} - \widehat {yOz'} = {180^0} - {45^0} = {135^0}\)

Lại có hai góc z’Om và tOz là hai góc đối đỉnh

=> \(\widehat {z'Om} = \widehat {tOz} = {135^0}\)

=> x = 135⁰

Phần Bài tập

Bài 1 trang 94 SGK Toán 7 tập 1 Cánh diều

a) Tìm hai góc kề nhau trong mỗi hình 18a, 18b:

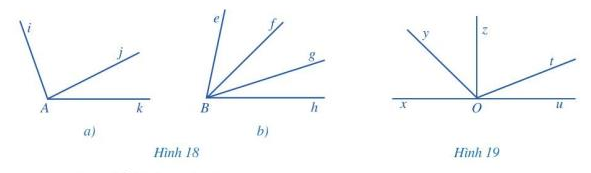
b) Tìm hai góc kề bù ở Hình 19.

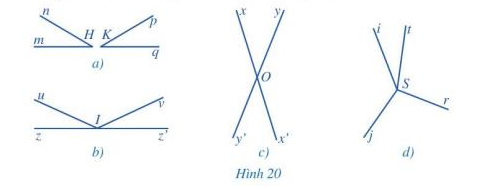
c) Tìm hai góc đối đỉnh trong mỗi hình 20a, 20b, 20c, 20d:

Gợi ý đáp án

a) Hai góc kề nhau:

Trong hình 18a là: góc iAj và góc jAk

Trong hình 18b là: góc eBf và góc fBg; góc eBf và góc fBh; góc eBg và góc gBh; góc fBg và góc gBh

b) 2 góc kề bù trong Hình 19 là: góc xOy và góc yOu; góc xOz và góc zOu; góc xOt và góc tOu

c) 2 góc đối đỉnh:

Trong Hình 20a: Không có vì 2 góc này không có chung đỉnh

Trong Hình 20b: Không có vì không có 2 góc nào mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

Trong Hình 20c: góc xOy và góc x’Oy’

Trong Hình 20d: Không có vì không có 2 góc nào mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

Bài 2 trang 95 SGK Toán 7 tập 1 Cánh diều

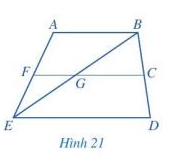
Quan sát Hình 21 và chỉ ra:

Gợi ý đáp án

a) 2 góc kề nhau là: góc ABE và EBD; góc AFG và GFE; góc AEB và BED; góc BCG và GCD; góc FGB và BGC; góc BGC và CGE; góc CGE và EGF; góc EGF và FGB.

b) 2 góc kề bù là: góc AFG và GFE; góc BCG và GCD; góc FGB và BGC; góc BGC và CGE; góc CGE và EGF; góc EGF và FGB.

c) 2 góc đối đỉnh là: góc FGB và CGE; góc BGC và EGF

Bài 3 trang 95 SGK Toán 7 tập 1 Cánh diều

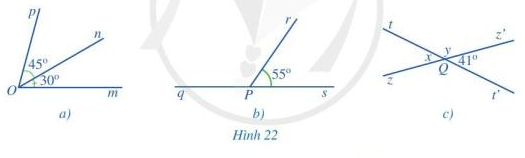
Tìm số đo:

a) Góc mOp trong Hình 22a;

b) Góc qPr trong Hình 22b;

c) x,y trong Hình 22c.

Gợi ý đáp án

a) Vì tia On nằm trong góc mOp nên \(\widehat {mOn} + \widehat {nOp} = \widehat {mOp}\)

\(\begin{array}{l} \Rightarrow 30^\circ + 45^\circ = \widehat {mOp}\\ \Rightarrow 75^\circ = \widehat {mOp}\end{array}\)

Vậy số đo góc mOp là 75 độ

b) Ta có:\(\widehat {q\Pr } + \widehat {rPs} = 180^\circ\) (2 góc kề bù)

\(\begin{array}{l} \Rightarrow \widehat {q\Pr } + 55^\circ = 180^\circ \\ \Rightarrow \widehat {q\Pr } = 180^\circ - 55^\circ = 125^\circ \end{array}\)

Vậy số đo góc qPr là 125 độ

c) Ta có: \(\widehat {tQz} = \widehat {t'Qz'}\) ( 2 góc đối đỉnh), mà \(\widehat {t'Qz'} = 41^\circ \Rightarrow \widehat {tQz} = 41^\circ\)

\(\widehat {tQz'} + \widehat {z'Qt'} = 180^\circ\) ( 2 góc kề bù) nên \(\widehat {tQz'} + 41^\circ = 180^\circ \Rightarrow \widehat {tQz'} = 180^\circ - 41^\circ = 139^\circ\)

Vậy \(x = 41 ^\circ ; y = 139 ^\circ\)

Bài 4 trang 95 SGK Toán 7 tập 1 Cánh diều

Hình 23 là một mẫu cửa có vòm tròn của một ngôi nhà. Nếu coi mỗi thanh chắn vòm cửa đó như một cạnh của góc thì các thanh chắn đó tạo ra các góc kề nhau. Theo em, mỗi góc tạo bởi hai thanh chắn vòm cửa đó khoảng bao nhiêu độ?

Gợi ý đáp án

Có 4 góc kề nhau được tạo thành, xếp thành góc bẹt, mỗi góc tạo bởi 2 thanh chắn vòm cửa

Nên mỗi góc có số đo: \(180^\circ : 4 = 45^\circ\)

Lý thuyết Góc ở vị trí đặc biệt

1. 2 góc kề bù

Hai góc có một cạnh chung, 2 cạnh còn lại là hai tia đối nhau được gọi là 2 góc kề bù.

* Tính chất: 2 góc kề bù có tổng số đo là 180 độ.

Góc xOz và góc yOz là 2 góc kề bù vì có tia Oz chung; tia Ox và Oy là 2 tia đối nhau.

Ta có: \(\widehat {xOz} + \widehat {yOz} = 180^\circ\)

Chú ý:

Nếu điểm M nằm trong góc xOy thì ta nói tia OM nằm giữa 2 tia Ox và Oy. Khi đó:

\(\widehat {xOM} + \widehat {MOy} = \widehat {xOy}\)

2. 2 góc đối đỉnh

2 góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

* Tính chất: Hai góc đối đỉnh thì bằng nhau

Chú ý: 2 đường thẳng cắt nhau tạo thành 2 cặp góc đối đỉnh

Ví dụ:

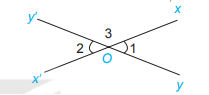
\(\widehat {{O_1}} = \widehat {{O_2}};\widehat {{O_3}} = \widehat {{O_4}}\) ( đối đỉnh)

Chú ý: 2 đường thẳng cắt nhau và trong các góc tạo thành có một góc vuông thì 2 đường thẳng đó vuông góc.

Ví dụ:

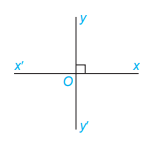
Hai đường thẳng xx' và yy' cắt nhau tại O, tạo thành 1 góc vuông. Ta nói hai đường thẳng xx' và yy' vuông góc với nhau.

Kí hiệu: xx'\(\bot\) yy' hoặc yy' \(\bot\) xx'