Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác Giải Toán lớp 7 trang 104, 105, 106 - Tập 2 sách Cánh diều

Bài trước

Mục lục

Bài sau

Giải Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác Cánh diều là tài liệu vô cùng hữu ích giúp các em học sinh lớp 7 có thêm nhiều gợi ý tham khảo để giải các bài tập từ 1→5 trang 104, 105, 106 tập 2.

Giải bài tập Toán 7 Cánh diều tập 2 trang 104, 105, 106 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài, đồng thời là tư liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy sau đây là nội dung chi tiết Giải Toán 7 bài 10 trang 104, 105, 106 Cánh diều, mời các bạn cùng theo dõi.

Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác

Giải Toán 7 trang 104, 105, 106 Cánh diều

Giải Toán 7 trang 104, 105, 106 Cánh diều

Bài 1

Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh:

GA + GB + GC = $\dfrac{2}{3}(AM + BN + CP)$ $\dfrac{2}{3}(AM + BN + CP)$.

Gợi ý đáp án

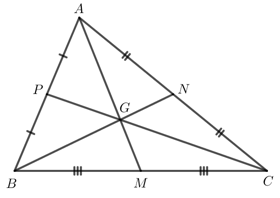
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng $\dfrac{2}{3}$ $\dfrac{2}{3}$độ dài đường trung tuyến đi qua đỉnh ấy nên:

$\begin{array}{l}\dfrac{{GA}}{{AM}} = \dfrac{{GB}}{{BN}} = \dfrac{{GC}}{{CP}} = \dfrac{2}{3}\\ \to GA = \dfrac{2}{3}AM;GB = \dfrac{2}{3}BN;GC = \dfrac{2}{3}CP\end{array}$ $\begin{array}{l}\dfrac{{GA}}{{AM}} = \dfrac{{GB}}{{BN}} = \dfrac{{GC}}{{CP}} = \dfrac{2}{3}\\ \to GA = \dfrac{2}{3}AM;GB = \dfrac{2}{3}BN;GC = \dfrac{2}{3}CP\end{array}$

Vậy:

$GA + GB + GC = \dfrac{2}{3}AM + \dfrac{2}{3}BN + \dfrac{2}{3}CP = \dfrac{2}{3}(AM + BN + CP).$ $GA + GB + GC = \dfrac{2}{3}AM + \dfrac{2}{3}BN + \dfrac{2}{3}CP = \dfrac{2}{3}(AM + BN + CP).$

Bài 2

Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:

a) BM = CN; b) $\Delta GBC$ $\Delta GBC$ cân tại G.

Gợi ý đáp án

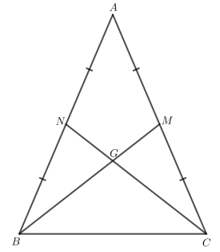
a) Tam giác ABC cân tại A nên AB = AC. M, N lần lượt là trung điểm của cạnh AC, AB nên AM = AN.

Xét tam giác ABM và tam giác ACN có: AM = AN; $\widehat A$ $\widehat A$ chung; AB = AC.

Vậy $\Delta ABM = \Delta ACN$ $\Delta ABM = \Delta ACN$(c.g.c) hay BM = CN.

b) G là giao điểm của hai đường trung tuyến BM và CN nên G là trọng tâm tam giác ABC. Hay:

$GB = \dfrac{2}{3}BM$ $GB = \dfrac{2}{3}BM$; $GC = \dfrac{2}{3}CN$ $GC = \dfrac{2}{3}CN$. Mà BM = CN nên GB = GC.

Vậy tam giác GBC cân tại G.

Bài 3

Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Trên tia đối của tia MA lấy điểm D sao cho MD = MG. Chứng minh:

a) GA = GD;

b) $\Delta MBG = \Delta MCD;$ $\Delta MBG = \Delta MCD;$

c) CD = 2GN.

Gợi ý đáp án

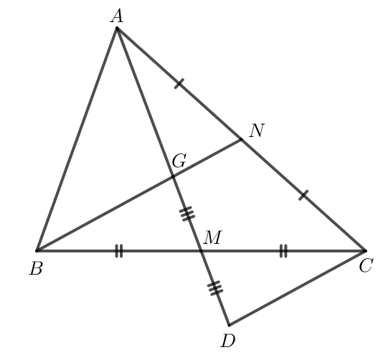
a) G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC.

Suy ra: AG = 2GM. Mà trên tia đối của tia MA lấy điểm D sao cho MD = MG nên GD = 2GM.

Vậy GA = GD (= 2GM).

b) Xét hai tam giác MBG và MCD có:

MB = MC (M là trung điểm cạnh BC)

$\widehat {GMB} = \widehat {DMC}$ $\widehat {GMB} = \widehat {DMC}$ (đối đỉnh)

GM = GD.

Vậy $\Delta MBG = \Delta MCD(c.g.c).$ $\Delta MBG = \Delta MCD(c.g.c).$

c) $\Delta MBG = \Delta MCD$ $\Delta MBG = \Delta MCD$ nên BG = CD (2 cạnh tương ứng).

Mà G là trọng tâm tam giác ABC nên BG = 2GN. Mà BG = CD nên CD = 2GN.

Bài 4

Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Gọi H là hình chiếu của A lên đường thẳng BC. Giả sử H là trung điểm của đoạn thẳng BM. Chứng minh:

a) $\Delta AHB = \Delta AHM$ $\Delta AHB = \Delta AHM$; b) AG = $\dfrac{2}{3}AB$ $\dfrac{2}{3}AB$.

Gợi ý đáp án

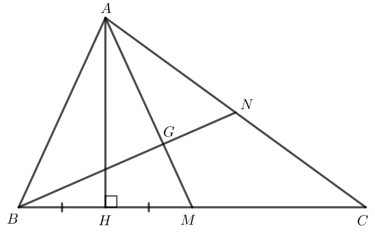
a) Xét tam giác AHB và tam giác AHM có:

AH chung;

$\widehat {AHB} = \widehat {AHM}$ $\widehat {AHB} = \widehat {AHM}$ (H là hình chiếu của A lên BC nên $AH \bot BC$ $AH \bot BC$);

HB = HM (H là trung điểm của BM).

Vậy $\Delta AHB = \Delta AHM$ $\Delta AHB = \Delta AHM$(c.g.c).

b) $\Delta AHB = \Delta AHM$ $\Delta AHB = \Delta AHM$nên AB = AM ( 2 cạnh tương ứng).

G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC. Nên: $AG = \dfrac{2}{3}AM$ $AG = \dfrac{2}{3}AM$.

Mà AB = AM suy ra: $AG = \dfrac{2}{3}AB$ $AG = \dfrac{2}{3}AB$.

Bài 5

Hình 107 là mặt cắt đứng của một ngôi nhà ba tầng có mái dốc. Mỗi tầng cao 3,3 m. Mặt cắt mái nhà có dạng tam giác ABC cân tại A với đường trung tuyến AH dài 1,2 m. Tại vị trí O là trọng tâm tam giác ABC, người ta làm tâm cho một cửa sổ có dạng hình tròn.

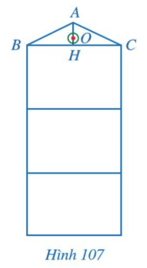
a) AH có vuông góc với BC không? Vì sao?

b) Vị trí O ở độ cao bao nhiêu mét so với mặt đất.

Gợi ý đáp án

a) Vì $\Delta ABC$ $\Delta ABC$ cân tại A nên AB = AC

Vì AH là đường trung tuyến của tam giác ABC nên BH = HC = $\dfrac{1}{2}. BC$ $\dfrac{1}{2}. BC$

Xét $\Delta ABH$ $\Delta ABH$ và $\Delta ACH$ $\Delta ACH$ có:

AH chung

AB = AC

BH = HC

$\Rightarrow \Delta ABH=\Delta ACH (c.c.c)$ $\Rightarrow \Delta ABH=\Delta ACH (c.c.c)$

$\Rightarrow \widehat{AHB}=\widehat{AHC}$ $\Rightarrow \widehat{AHB}=\widehat{AHC}$ ( 2 góc tương ứng)

Mà $\widehat{AHB}+\widehat{AHC}=180^0$ $\widehat{AHB}+\widehat{AHC}=180^0$

$\Rightarrow \widehat{AHB}=\widehat{AHC}=180^0 : 2 = 90^0$ $\Rightarrow \widehat{AHB}=\widehat{AHC}=180^0 : 2 = 90^0$

Vậy AH có vuông góc với BC.

b) Vị trí O ở độ cao so với mặt đất bằng độ cao ba tầng cộng với khoảng cách OH.

Độ cao ba tầng của tòa nhà bằng 3,3.3 = 9,9(m).

Mà O là trọng tâm tam giác ABC nên $OH = \dfrac{1}{3}AH$ $OH = \dfrac{1}{3}AH$. Vậy $OH = \dfrac{1}{3}.1,2 = 0,4(m).$ $OH = \dfrac{1}{3}.1,2 = 0,4(m).$

Vậy vị trí O ở độ cao: 9,9 + 0,4 = 10,3m so với mặt đất.

Chia sẻ bởi: