Toán 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ Giải Toán lớp 7 trang 16 - Tập 1 sách Cánh diều

Giải Toán lớp 7 trang 16 tập 1 Cánh diều giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần Luyện tập vận dụng và 7 bài tập thuộc bài 2 Cộng, trừ, nhân, chia số hữu tỉ được nhanh chóng và dễ dàng hơn.

Toán 7 Cánh diều tập 1 trang 16 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 7. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 7 Cộng, trừ, nhân, chia số hữu tỉ trang 16 Cánh diều mời các bạn cùng theo dõi.

Phần Luyện tập và vận dụng

Luyện tập 1 trang 13 Toán 7 tập 1

Tính

Gợi ý đáp án

Thực hiện phép tính như sau:

a) \(\frac{5}{7} - \left( { - 3,9} \right)\)

\(= \frac{5}{7} + 3,9 = \frac{5}{7} + \frac{{39}}{{10}} = \frac{{50}}{{70}} + \frac{{273}}{{70}} = \frac{{323}}{{70}}\)

b) \(\left( { - 3,25} \right) + 4\frac{3}{4}\)

\(= - \frac{{13}}{4} + \frac{{19}}{4} = \frac{6}{4} = \frac{3}{2}\)

Luyện tập 2 trang 13 Toán 7 tập 1

Tính một cách hợp lí:

Gợi ý đáp án

a) \(\left( { - 0,4} \right) + \frac{3}{8} + \left( { - 0,6} \right)\)

\(\begin{matrix} = \left[ {\left( { - 0,4} \right) + \left( { - 0,6} \right)} \right] + \dfrac{3}{8} \hfill \\ = - 1 + \dfrac{3}{8} = \dfrac{{ - 8}}{8} + \dfrac{3}{8} = \dfrac{{ - 5}}{8} \hfill \\ \end{matrix}\)

b) \(\frac{4}{5} - 1,8 + 0,375 + \frac{5}{8}\)

\(\begin{matrix} = \dfrac{4}{5} - \dfrac{9}{5} + \dfrac{3}{8} + \dfrac{5}{8} \hfill \\ = \left( {\dfrac{4}{5} - \dfrac{9}{5}} \right) + \left( {\dfrac{3}{8} + \dfrac{5}{8}} \right) \hfill \\ = \dfrac{{ - 5}}{5} + \dfrac{8}{8} = - 1 + 1 = 0 \hfill \\ \end{matrix}\)

Luyện tập 3 trang 14 Toán 7 tập 1

Tìm x , biết:

Gợi ý đáp án

a) \(x - \left( { - \frac{7}{9}} \right) = - \frac{5}{6}\)

\(\begin{matrix} x = - \dfrac{5}{6} + \left( { - \dfrac{7}{9}} \right) \hfill \\ x = - \dfrac{5}{6} - \dfrac{7}{9} \hfill \\ x = - \dfrac{{15}}{{18}} - \dfrac{{14}}{{18}} \hfill \\ x = - \dfrac{{29}}{{18}} \hfill \\ \end{matrix}\)

Vậy \(x = - \frac{{29}}{{18}}\)

b) \(\frac{{15}}{{ - 4}} - x = 0,3\)

\(\begin{matrix} x = \dfrac{{15}}{{ - 4}} - 0,3 \hfill \\ x = \dfrac{{15}}{{ - 4}} - \dfrac{3}{{10}} \hfill \\ x = \dfrac{{ - 75}}{{20}} - \dfrac{6}{{20}} \hfill \\ x = \dfrac{{ - 81}}{{20}} \hfill \\ \end{matrix}\)

Vậy \(x = \frac{{ - 81}}{{20}}\)

Luyện tập 4 trang 14 Toán 7 tập 1

Giải bài toán nêu trong phần mở đầu:

Đèo Hải Vân là một cung đường hiểm trở trên tuyến giao thông xuyên suốt Việt Nam. Để thuận lợi cho việc đi lại, người ta đã xây dựng hầm đường bộ xuyên đèo Hải Vân.

Hầm Hải Vân có chiều dài 6,28km và bằng \(\frac{{157}}{{500}}\) độ dài của đèo Hải Vân.

Độ dài đèo Hải Vân là bao nhiêu ki – lô – mét?

Gợi ý đáp án

Ta có:

Hầm Hải Vân có chiều dài 6,25km và bằng \(\frac{{157}}{{500}}\) độ dài của đèo Hải Vân.

Độ dài đèo Hải Vân là:

\(6,28:\frac{{157}}{{500}} = 6,28.\frac{{500}}{{157}} = 20\) (km)

Vậy đèo Hải Vân dài 20km.

Luyện tập 5 trang 14 Toán 7 tập 1

Một ô tô đi từ tỉnh A đến tính B. Trong một giờ đầu, ô tô đã đi được \(\frac{2}{5}\) quãng đường. Hỏi với vận tốc đó, ô tô phải mất bao lâu để đi hết quãng đường AB?

Gợi ý đáp án

Quãng đường còn lại là: \(1 - \frac{2}{5} = \frac{3}{5}\)

Trong 1 giờ người đó đi được \(\frac{2}{5}\) quãng đường

Suy ra quãng đường còn lại người đó đi trong thời gian là:

\(\frac{3}{5}:\frac{2}{5} = \frac{3}{5}.\frac{5}{2} = \frac{3}{2}\) (giờ)

Vậy người đó đi trong 1,5 giờ thì đi hết quãng đường còn lại.

Luyện tập 6 trang 16 Toán 7 tập 1

Tính một cách hợp lí:

Gợi ý đáp án

a) \(\frac{7}{3}.\left( { - 2,5} \right).\frac{6}{7}\)

\(\begin{matrix} = \dfrac{7}{3}.\left( {\dfrac{{ - 25}}{{10}}} \right).\dfrac{6}{7} \hfill \\ = \left( {\dfrac{7}{3}.\dfrac{6}{7}} \right).\left( {\dfrac{{ - 25}}{{10}}} \right) \hfill \\ = 2.\left( {\dfrac{{ - 5}}{2}} \right) = - 5 \hfill \\ \end{matrix}\)

b) \(0,8.\frac{{ - 2}}{9} - \frac{4}{5}.\frac{7}{9} - 0,2\)

\(\begin{matrix} = \dfrac{8}{{10}}.\dfrac{{ - 2}}{9} - \dfrac{8}{{10}}.\dfrac{7}{9} - \dfrac{1}{5} \hfill \\ = \dfrac{4}{5}.\dfrac{{ - 2}}{9} - \dfrac{4}{5}.\dfrac{7}{9} - \dfrac{1}{5} \hfill \\ = \dfrac{4}{5}.\left( {\dfrac{{ - 2}}{9} - \dfrac{7}{9}} \right) - \dfrac{1}{5} \hfill \\ = \dfrac{4}{5}.\left( {\dfrac{{ - 9}}{9}} \right) - \dfrac{1}{5} \hfill \\ = \dfrac{4}{5}.\left( { - 1} \right) - \dfrac{1}{5} = - \dfrac{4}{5} - \dfrac{1}{5} = - 1 \hfill \\ \end{matrix}\)

Luyện tập 7 trang 16 Toán 7 tập 1

Tìm số nghịch đảo của mỗi số hữu tỉ sau:

Gợi ý đáp án

a) Ta có: \(2\frac{1}{5} = \frac{{2.5 + 1}}{5} = \frac{{11}}{5}\)

Khi đó số nghịch đảo của số \(\frac{{11}}{5}\) là số \(1:\frac{{11}}{5} = 1.\frac{5}{{11}} = \frac{5}{{11}}\)

Vậy số nghịch đảo của số \(2\frac{1}{5}\) là \(\frac{5}{{11}}\)

b) Ta có: \(- 13 = \frac{{ - 13}}{1}\)

Khi đó số nghịch đảo của số \(- \frac{{13}}{1}\) là số \(1:\left( { - \frac{{13}}{1}} \right) = 1.\left( { - \frac{1}{{13}}} \right) = \frac{{ - 1}}{{13}}\)

Vậy số nghịch đảo của số -13 là \(- \frac{1}{{13}}\)

Phần Bài tập

Bài 1 trang 16 Toán 7 tập 1

Tính:

Gợi ý đáp án 

a) \(\frac{{ - 1}}{6} + 0,75 = \frac{{ - 1}}{6} + \frac{{75}}{{100}} = \frac{{ - 1}}{6} + \frac{3}{4} = \frac{{ - 2}}{{12}} + \frac{9}{{12}} = \frac{7}{{12}}\)

b) \(3\frac{1}{{10}} - \frac{3}{8} = \frac{{31}}{{10}} - \frac{3}{8} = \frac{{124}}{{40}} - \frac{{15}}{{40}} = \frac{{109}}{{40}}\)

c) \(0,1 + \frac{{ - 9}}{{17}} - \left( { - 0,9} \right)\)

\(\begin{matrix} = 0,1 + \dfrac{{ - 9}}{{17}} - \left( { - 0,9} \right) \hfill \\ = \dfrac{1}{{10}} + \dfrac{{ - 9}}{{17}} + \dfrac{9}{{10}} \hfill \\ = \left( {\dfrac{1}{{10}} + \dfrac{9}{{10}}} \right) + \dfrac{{ - 9}}{{17}} \hfill \\ = \dfrac{{10}}{{10}} - \dfrac{9}{{17}} = 1 - \dfrac{9}{{17}} \hfill \\ = \dfrac{{17}}{{17}} - \dfrac{9}{{17}} = \dfrac{8}{{17}} \hfill \\ \end{matrix}\)

Bài 2 trang 16 Toán 7 tập 1

Tính:

Gợi ý đáp án

a) \(5,75.\frac{{ - 8}}{9} = \frac{{575}}{{100}}.\frac{{ - 8}}{9} = \frac{{ - 46}}{9}\)

b) \(2\frac{3}{8}.\left( { - 0,4} \right) = \frac{{19}}{8}.\frac{{ - 4}}{{10}} = - \frac{{19}}{{20}}\)

c) \(\frac{{ - 12}}{5}:\left( { - 6,5} \right) = \frac{{ - 12}}{5}:\frac{{ - 65}}{{10}} = \frac{{ - 12}}{5}.\frac{{10}}{{ - 45}} = \frac{8}{{15}}\)

Bài 3 trang 16 Toán 7 tập 1

Tính một cách hợp lí:

Gợi ý đáp án 

a) \(\frac{{ - 3}}{{10}} - 0,125 + \frac{{ - 7}}{{10}} + 1,125\)

\(\begin{matrix} = \left( {\dfrac{{ - 3}}{{10}} + \dfrac{{ - 7}}{{10}}} \right) + \left( { - 0,125 + 1,125} \right) \hfill \\ = \dfrac{{ - 10}}{{10}} + 0 = - 1 + 0 = - 1 \hfill \\ \end{matrix}\)

b) \(\frac{{ - 8}}{3}.\frac{2}{{11}} - \frac{8}{3}:\frac{{11}}{9}\)

\(\begin{matrix} = \dfrac{{ - 8}}{3}.\dfrac{2}{{11}} - \dfrac{8}{3}.\dfrac{9}{{11}} \hfill \\ = \dfrac{8}{3}.\left( {\dfrac{{ - 2}}{{11}} - \dfrac{9}{{11}}} \right) \hfill \\ = \dfrac{8}{3}.\left( {\dfrac{{ - 11}}{{11}}} \right) = \dfrac{8}{3}.\left( { - 1} \right) = \dfrac{{ - 8}}{3} \hfill \\ \end{matrix}\)

Bài 4 trang 14 Toán 7 tập 1

Tìm x biết:

Gợi ý đáp án

Bài 5 trang 14 Toán 7 tập 1

Bác Nhi gửi vào ngân hàng 60 triệu đồng với kì hạn 1 năm, lãi suất 6,5%/năm. Hết kì hạn 1 năm, bác rút ra \(\frac{1}{3}\) số tiền (kể cả gốc và lãi). Tính số tiền còn lại của bác Nhi trong ngân hàng.

Gợi ý đáp án

Hết kì hạn 1 năm số tiền lãi bác Nhi nhận được là:

6,5 . 60 000 000 : 100 = 3 900 000 (đồng)

Hết kì hạn 1 năm số tiền bác Nhi nhận được (cả gốc và lãi) là:

60 000 000 + 3 900 000 = 63 900 000 (đồng)

Bác Nhi rút ra \(\frac{1}{3}\) số tiền (cả gốc và lãi) tương ứng với:

\(\frac{1}{3}.63{\text{ }}900{\text{ }}000 = 21{\text{ }}300{\text{ }}000\) (đồng)

Số tiền bác Nhi còn lại trong ngân hàng là:

63 900 000 – 21 300 000 = 38 700 000(đồng)

Vậy số tiền còn lại của bác Nhi trong ngân hàng là 38 700 000 đồng.

Bài 6 trang 14 Toán 7 tập 1

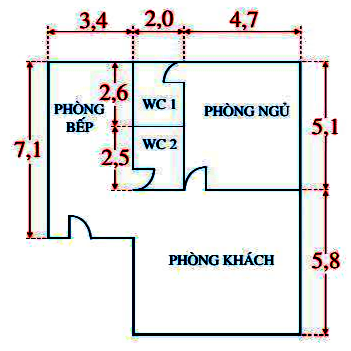
Tính diện tích mặt bằng của ngôi nhà trong hình vẽ bên (các số đo trên hình tính theo đơn vị mét)

Gợi ý đáp án

Diện tích mặt bằng của ngôi nhà bằng diện tích hình ABCDEF.

Độ dài đoạn thẳng AB là: 3,4 + 2,0 + 4,7 = 10,1 (m)

Độ dài đoạn thẳng BC là: 5,1 + 5,8 = 10,9 (m)

FG = BC- AF = 10,9 – 7,1 = 3,8 (m)

Diện tích hình chữ nhật ABCG là: 10,1 . 10,9 = 110,09 (m²)

Diện tích hình chữ nhật FEDG là: 3,8 . 3,4 = 12,92 (m²)

Diện tích mặt bằng của ngôi nhà (diện tích hình ABCDEF) là:

110,09 – 12,92 = 97,17 (m²)

Vậy diện tích mặt bằng của ngôi nhà trong hình vẽ là 97,17m²

Bài 7 trang 16 Toán 7 tập 1

Theo yêu cầu của kiến trúc sư, khoảng cách tối thiểu giữa ổ cắm điện và vòi nước của nhà chú Năm là 60cm. Trên bản vẽ có tỉ lệ \(\frac{1}{{20}}\) của thiết kế nhà chú Năm, khoảng cách từ ổ cắm điện đến vòi nước đo được là 2,5cm. Khoảng cách trên bản vẽ như vậy có phù hợp với yêu cầu của kiến trúc sư hay không? Giải thích vì sao?

Gợi ý đáp án

Khoảng cách thực tế từ ổ điện đến vòi nước tính từ bản vẽ là:

2,5 . 20 = 50 (cm)

Theo bài ra ta có:

Khoảng cách tối thiểu giữa ổ cắm điện và vòi nước của nhà chú Năm là 60cm

Nghĩa là khoảng cách lớn hơn hoặc bằng 60cm

Do 50cm < 60cm

Vậy khoảng cách trên bản vẽ không phù hợp với yêu cầu của kiến trúc sư

Lý thuyết Cộng, trừ, nhân, chia số hữu tỉ

1. Quy tắc cộng, trừ hai số hữu tỉ

Ta có thể cộng, trừ hai số hữu tỉ x, y bằng cách viết chúng dưới dạng hai phân số rồi áp dụng quy tắc cộng, trừ phân số

Với \(x = \frac{p}{m};y = \frac{q}{m};\left( {p,q,m \in \mathbb{Z},m > 0} \right)\) ta có:

\(x + y = \frac{p}{m} + \frac{q}{m} = \frac{{p + q}}{m}\)

\(x - y = \frac{p}{m} - \frac{q}{m} = \frac{{p - q}}{m}\)

2. Tính chất

- Phép cộng số hữu tỉ có tính chất của phép cộng phân số: Giao hoán, kết hợp, cộng với 0, cộng với số đối.

- Với \(a,b,c \in \mathbb{Q}\) ta có:

a) Tính chất giao hoán: a + b = b + a

b) Tính chất kết hợp: a + (b + c) = (a + b) + c

c) Cộng với số 0: a + 0 = 0 + a = a

d) Cộng với số đối: a + (-a) = 0

3. Quy tắc chuyển vế

Khi chuyển vế một số hạng tử từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó.

Trong Q ta có tổng đại số, trong đó có thể đổi chỗ các số hạng, đặt dấu ngoặc để nhóm các số hạng một cách tùy ý như các tổng đại số trong Z

Với \(a,b,c \in \mathbb{Q}\) nếu a + b = c thì a = -b + c

Với \(a,b,c \in \mathbb{Q}\) ta có:

x – (y – z) = x – y + z = x + z – y

x – y + z = x – (y – z)