Toán 7 Bài 1: Tập hợp các số hữu tỉ Giải Toán lớp 7 trang 5 - Tập 1 sách Kết nối tri thức

Bài trước

Mục lục

Bài sau

Giải bài tập Toán lớp 7 Bài 1: Tập hợp các số hữu tỉ với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 5, 6, 7, 8, 9. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 7 Bài 1 chi tiết phần câu hỏi, luyện tập, bài tập, đồng thời còn giúp các em hệ thống lại toàn bộ kiến thức lý thuyết trọng tâm của Bài 1 Chương I: Số hữu tỉ. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 7 bài 1: Tập hợp các số hữu tỉ sách Kết nối tri thức

Phần Luyện tập

Luyện tập 1 trang 6 Toán 7 tập 1

Giải thích vì sao các số 8, -3,3; $3\frac{2}{3}$ $3\frac{2}{3}$ đều là các số hữu tỉ. Tìm số đối của mỗi số đó.

Lời giải:

(1) Ta có: $8 = \frac{8}{1}$ $8 = \frac{8}{1}$

Vì $8 \in \mathbb{Z},1 \in \mathbb{Z},1 \ne 0$ $8 \in \mathbb{Z},1 \in \mathbb{Z},1 \ne 0$

Vậy 8 là số hữu tỉ

Số đối của số 8 là -8

(2) Ta có: $- 3,3 = \frac{{ - 33}}{{10}}$ $- 3,3 = \frac{{ - 33}}{{10}}$

Vì $- 33 \in \mathbb{Z},10 \in \mathbb{Z},10 \ne 0$ $- 33 \in \mathbb{Z},10 \in \mathbb{Z},10 \ne 0$

Vậy -3,3 là số hữu tỉ

Số đối của số -3,3 là –(–3,3) = 3,3

(3) Ta có: $3\frac{2}{3} = \frac{{11}}{3}$ $3\frac{2}{3} = \frac{{11}}{3}$

Vì $11 \in \mathbb{Z},3 \in \mathbb{Z},3 \ne 0$ $11 \in \mathbb{Z},3 \in \mathbb{Z},3 \ne 0$

Vậy $3\frac{2}{3}$ $3\frac{2}{3}$ là số hữu tỉ

Số đối của số $3\frac{2}{3}$ $3\frac{2}{3}$ là $- 3\frac{2}{3}$ $- 3\frac{2}{3}$

Luyện tập 2 trang 7 Toán 7 tập 1

Biểu diễn các số hữu tỉ $\frac{5}{4}$ $\frac{5}{4}$ và $\frac{{ - 5}}{4}$ $\frac{{ - 5}}{4}$ trên trục số.

Lời giải:

Chia đoạn thẳng đơn vị thành 4 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng $\frac{1}{4}$ $\frac{1}{4}$ đơn vị cũ.

Lấy một điểm nằm trước gốc O và cách O một đoạn bằng 5 đơn vị mới. Điểm đó biểu diễn số hữu tỉ − $\frac{-5}{4}$ $\frac{-5}{4}$

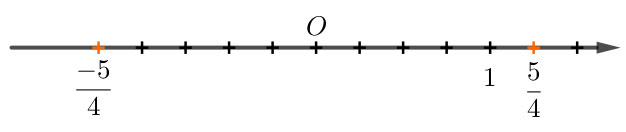
Lấy một điểm nằm sau gốc O và cách O một đoạn bằng 5 đơn vị mới. Điểm đó biểu diễn số hữu tỉ $\frac{5}{4}$ $\frac{5}{4}$.

Mô tả hình vẽ minh họa:

Trục số

Luyện tập 3 trang 8 Toán 7 tập 1

Sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn:

$5\frac{1}{4};{\text{ }} - 2;{\text{ }}3,125;{\text{ }} - \frac{3}{2}$ $5\frac{1}{4};{\text{ }} - 2;{\text{ }}3,125;{\text{ }} - \frac{3}{2}$

Lời giải:

Cách 1: Đưa bài toán về dạng so sánh các số thập phân:

$\begin{matrix} 5\dfrac{1}{4} = \dfrac{{21}}{4} = 5,25 \hfill \\ - \dfrac{3}{2} = - 1,5 \hfill \\ \end{matrix}$ $\begin{matrix} 5\dfrac{1}{4} = \dfrac{{21}}{4} = 5,25 \hfill \\ - \dfrac{3}{2} = - 1,5 \hfill \\ \end{matrix}$

Ta có: -2 < -1,5 < 0 < 3,125 < 5,25

Suy ra $- 2 < \frac{{ - 3}}{2} < 3,125 < 5\frac{1}{4}$ $- 2 < \frac{{ - 3}}{2} < 3,125 < 5\frac{1}{4}$

Vậy sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn như sau: $- 2;\frac{{ - 3}}{2};3,125;5\frac{1}{4}$ $- 2;\frac{{ - 3}}{2};3,125;5\frac{1}{4}$

Cách 2: Đưa bài toán về dạng so sánh các phân số có cùng mẫu số:

Ta có:

$\begin{matrix} 3,125 = \dfrac{{3125}}{{1000}} = \dfrac{{3125:125}}{{3125:125}} = \dfrac{{25}}{8} \hfill \\ 5\dfrac{1}{4} = \dfrac{{21}}{4} = \dfrac{{ - 42}}{8} \hfill \\ - 2 = \dfrac{{ - 2}}{1} = \dfrac{{ - 16}}{8} \hfill \\ - \dfrac{3}{2} = \dfrac{{ - 12}}{8} \hfill \\ \end{matrix}$ $\begin{matrix} 3,125 = \dfrac{{3125}}{{1000}} = \dfrac{{3125:125}}{{3125:125}} = \dfrac{{25}}{8} \hfill \\ 5\dfrac{1}{4} = \dfrac{{21}}{4} = \dfrac{{ - 42}}{8} \hfill \\ - 2 = \dfrac{{ - 2}}{1} = \dfrac{{ - 16}}{8} \hfill \\ - \dfrac{3}{2} = \dfrac{{ - 12}}{8} \hfill \\ \end{matrix}$

Do $\frac{{ - 16}}{8} < \frac{{ - 12}}{8} < 0 < \frac{{25}}{8} < \frac{{42}}{8}$ $\frac{{ - 16}}{8} < \frac{{ - 12}}{8} < 0 < \frac{{25}}{8} < \frac{{42}}{8}$

Suy ra: $- 2 < \frac{{ - 3}}{2} < 0 < 3,125 < 5\frac{1}{4}$ $- 2 < \frac{{ - 3}}{2} < 0 < 3,125 < 5\frac{1}{4}$

Vậy sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn như sau: $- 2;\frac{{ - 3}}{2};3,125;5\frac{1}{4}$ $- 2;\frac{{ - 3}}{2};3,125;5\frac{1}{4}$

Phần Vận dụng

Em hãy giải bài toán mở đầu.

Chỉ số WHtR (Waist ti Height Ratio) của một người trưởng thành, được tính bằng tỉ số giữa số đo vòng bụng và chiều cao (cùng một đơn vị đo). Chỉ số này được coi là một công cụ đo lường sức khỏe hữu ích vì nó có thể dự báo được các nguy cơ béo phì, mắc bệnh tim mạch, …. Bảng bên cho biết nguy cơ thừa cân, béo phì của một người đàn ông trưởng thành dựa vào chỉ số WHtR

(Theo hospimedica.com)

Gầy	Chỉ số WHtR nhỏ hơn hoặc bằng 0,42
Tốt	Chỉ số WHtR lớn hơn 0,42 và nhỏ hơn hoặc bằng 0,52
Hơi béo	Chỉ số WHtR lớn hơn 0,52 và nhỏ hơn hoặc bằng 0,57
Thừa cân	Chỉ số WHtR lớn hơn 0,57 và nhỏ hơn hoặc bằng 0,63
Béo phì	Chỉ số WHtR lớn hơn 0,63

Ông An cao 180cm, vòng bụng 108cm.

Ông chung cao 160cm, vòng bụng 70cm.

Theo em, nếu tính theo chỉ số WHtR, sức khỏe của ông An hay ông Chung tốt hơn?

Gợi ý đáp án:

- Chỉ số WHtR của ông An là: $\frac{{108}}{{180}} = \frac{3}{5} = 0,6$ $\frac{{108}}{{180}} = \frac{3}{5} = 0,6$

Do 0,57 < 0, 6 < 0,63

=> Ông An thuộc nhóm người Thừa cân.

- Chỉ số WHtR của ông Chung là: $\frac{{70}}{{160}} = \frac{7}{{16}} = 0,4375$ $\frac{{70}}{{160}} = \frac{7}{{16}} = 0,4375$

Do 0,42 < 0, 4375 < 0,52

=> Ông An thuộc nhóm người có sức khỏe Tốt.

Vậy sức khỏe của ông Chung tốt hơn ông An.

Phần Bài tập

Bài 1.1 trang 9 Toán 7 tập 1

Khẳng định nào sau đây là đúng?

a) $0,25 \in \mathbb{Q}$ $0,25 \in \mathbb{Q}$

b) $- \frac{6}{7} \in \mathbb{Q}$ $- \frac{6}{7} \in \mathbb{Q}$

c) $- 235 \in \mathbb{Q}$ $- 235 \in \mathbb{Q}$

Gợi ý đáp án:

a) Ta có: $0,25 = \frac{{25}}{{100}} = \frac{{25:25}}{{100:25}} = \frac{1}{4}$ $0,25 = \frac{{25}}{{100}} = \frac{{25:25}}{{100:25}} = \frac{1}{4}$

Vì $1 \in \mathbb{Z},4 \in \mathbb{Z},4 \ne 0$ $1 \in \mathbb{Z},4 \in \mathbb{Z},4 \ne 0$ nên $0,25 \in \mathbb{Q}$ $0,25 \in \mathbb{Q}$

Vậy a là khẳng định đúng.

b) Vì $- 6 \in \mathbb{Z},7 \in \mathbb{Z},7 \ne 0$ $- 6 \in \mathbb{Z},7 \in \mathbb{Z},7 \ne 0$ nên $- \frac{6}{7} \in \mathbb{Q}$ $- \frac{6}{7} \in \mathbb{Q}$

Vậy b là khẳng định đúng.

c) Ta có: $- 235 = \frac{{ - 235}}{1}$ $- 235 = \frac{{ - 235}}{1}$

Vì $- 235 \in \mathbb{Z},1 \in \mathbb{Z},1 \ne 0$ $- 235 \in \mathbb{Z},1 \in \mathbb{Z},1 \ne 0$ nên $- 235 \in \mathbb{Q}$ $- 235 \in \mathbb{Q}$

Vậy c là khẳng định đúng.

Bài 1.2 trang 9 Toán 7 tập 1

Tìm số đối của các số hữu tỉ sau:

a) -0,75

b) $6\frac{1}{5}$ $6\frac{1}{5}$

Gợi ý đáp án:

a) Số đối của số hữu tỉ -0,75 là –(-0,75) = 0,75

b) Số đối của số hữu tỉ $6\frac{1}{5}$ $6\frac{1}{5}$ là $- 6\frac{1}{5}$ $- 6\frac{1}{5}$

Bài 1.3 trang 9 Toán 7 tập 1

Các điểm A, B, C, D (H.17) biểu diễn những số hữu tỉ nào?

H.17

Gợi ý đáp án:

- Đoạn thẳng đơn vị chia thành 6 đoạn thẳng bằng nhau, đơn vị mới bằng $\frac{1}{6}$ $\frac{1}{6}$ đơn vị cũ.

Quan sát phần hình vẽ phía bên phải điểm O:

+ Điểm C nằm cách O một đoạn bằng 3 đơn vị mới.

=> Điểm C biểu diễn số hữu tỉ: $\frac{3}{6} = \frac{1}{2} = 0,5$ $\frac{3}{6} = \frac{1}{2} = 0,5$

+ Điểm D nằm cách O một đoạn bằng 8 đơn vị mới

=> Điểm D biểu diễn số hữu tỉ: $\frac{8}{6} = \frac{4}{3}$ $\frac{8}{6} = \frac{4}{3}$

Quan sát phần hình vẽ phía bên trái điểm O (các số hữu tỉ là các số âm)

+ Điểm B nằm cách O một đoạn bằng 2 đơn vị mới.

=> Điểm B biểu diễn số hữu tỉ: $- \frac{2}{6} = - \frac{1}{3}$ $- \frac{2}{6} = - \frac{1}{3}$

+ Điểm A nằm cách O một đoạn bằng 7 đơn vị mới

=> Điểm A biểu diễn số hữu tỉ: $- \frac{7}{6}$ $- \frac{7}{6}$

Bài 1.4 trang 9 Toán 7 tập 1

a) Trong những phân số sau, những phân số nào biểu diễn số hữu tỉ -0,625?

$\frac{5}{{ - 8}};\frac{{10}}{{16}};\frac{{20}}{{ - 32}};\frac{{ - 10}}{{16}};\frac{{ - 25}}{{40}};\frac{{35}}{{ - 48}}$ $\frac{5}{{ - 8}};\frac{{10}}{{16}};\frac{{20}}{{ - 32}};\frac{{ - 10}}{{16}};\frac{{ - 25}}{{40}};\frac{{35}}{{ - 48}}$

b) Biểu diễn số hữu tỉ -0,625 trên trục số.

Gợi ý đáp án:

a) Ta có: $- 0,625 = - \frac{{625}}{{1000}} = - \frac{{625:125}}{{1000:125}} = - \frac{5}{8}$ $- 0,625 = - \frac{{625}}{{1000}} = - \frac{{625:125}}{{1000:125}} = - \frac{5}{8}$

Ta lại có:

$- \frac{5}{8} = \frac{{ - 5.2}}{{8.2}} = \frac{{ - 10}}{{16}}$ $- \frac{5}{8} = \frac{{ - 5.2}}{{8.2}} = \frac{{ - 10}}{{16}}$

$- \frac{5}{8} = \frac{{ - 5.4}}{{8.4}} = \frac{{ - 20}}{{32}}$ $- \frac{5}{8} = \frac{{ - 5.4}}{{8.4}} = \frac{{ - 20}}{{32}}$

$- \frac{5}{8} = \frac{{ - 5.5}}{{8.5}} = \frac{{ - 25}}{{40}}$ $- \frac{5}{8} = \frac{{ - 5.5}}{{8.5}} = \frac{{ - 25}}{{40}}$

Suy ra $- 0,625 = - \frac{5}{8} = \frac{{ - 10}}{{16}} = \frac{{ - 20}}{{32}} = \frac{{ - 25}}{{40}}$ $- 0,625 = - \frac{5}{8} = \frac{{ - 10}}{{16}} = \frac{{ - 20}}{{32}} = \frac{{ - 25}}{{40}}$

Vậy những phân số biểu diễn số hữu tỉ -0,625 là $- \frac{5}{8};\frac{{ - 10}}{{16}};\frac{{ - 20}}{{32}};\frac{{ - 25}}{{40}}$ $- \frac{5}{8};\frac{{ - 10}}{{16}};\frac{{ - 20}}{{32}};\frac{{ - 25}}{{40}}$

b) Theo câu a ta có: $- 0,625 = - \frac{5}{8}$ $- 0,625 = - \frac{5}{8}$ nên biểu diễn -0,625 trên trục số chính là biểu diễn phân số $- \frac{5}{8}$ $- \frac{5}{8}$ trên trục số.

Mô tả bằng hình vẽ như sau:

Hình vẽ

Bước 1: Chia đoạn thẳng đơn vị thành 8 phần bằng nhau.

Bước 2: Lấy một điểm nằm về phía bên trái điểm O một đoạn bằng 5 đơn vị (đơn vị mới bằng $\frac{1}{8}$ $\frac{1}{8}$ đơn vị cũ)

Ta được điểm biểu diễn số hữu tỉ $- \frac{5}{8} = - 0,625$ $- \frac{5}{8} = - 0,625$

Bài 1.5 trang 9 Toán 7 tập 1

So sánh:

a) -2,5 và -2,125

b) $- \frac{1}{{10000}}$ $- \frac{1}{{10000}}$ và $\frac{1}{{23456}}$ $\frac{1}{{23456}}$

Gợi ý đáp án:

a) -2,5 và -2,125

Ta có: 2,5 < 2,125

=> -2,5 > -2,125

Vậy -2,5 > -2,125

b) $- \frac{1}{{10000}}$ $- \frac{1}{{10000}}$ và $\frac{1}{{23456}}$ $\frac{1}{{23456}}$

Ta có: $- \frac{1}{{10000}} < 0$ $- \frac{1}{{10000}} < 0$ và $\frac{1}{{23456}} > 0$ $\frac{1}{{23456}} > 0$

=> $- \frac{1}{{10000}} < 0 < \frac{1}{{23456}}$ $- \frac{1}{{10000}} < 0 < \frac{1}{{23456}}$

=> $- \frac{1}{{10000}} < \frac{1}{{23456}}$ $- \frac{1}{{10000}} < \frac{1}{{23456}}$

Vậy $- \frac{1}{{10000}} < \frac{1}{{23456}}$ $- \frac{1}{{10000}} < \frac{1}{{23456}}$

Bài 1.6 trang 9 Toán 7 tập 1

Tuổi thị trung bình dự kiến của những người sinh năm 2019 ở một số quốc gia được cho trong bảng sau:

Quốc gia	Australia	Pháp	Tây Ban Nha	Anh	Mĩ
Tuổi thọ trung bình dự kiến	83	82,5	$83\frac{1}{5}$ $83\frac{1}{5}$	$81\frac{2}{5}$ $81\frac{2}{5}$	$78\frac{1}{2}$ $78\frac{1}{2}$