Toán 7 Bài 28: Phép chia đa thức một biến Giải Toán lớp 7 trang 39 sách Kết nối tri thức với cuộc sống - Tập 2
Giải bài tập SGK Toán 7 Tập 2 trang 39, 40, 41, 42, 43 sách Kết nối tri thức với cuộc sống giúp các em học sinh lớp 7 xem gợi ý giải các bài tập của Bài 28: Phép chia đa thức một biến.
Thông qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 28 Chương VII - Biểu thức đại số và đa thức một biến trong sách giáo khoa Toán 7 Tập 2 Kết nối tri thức với cuộc sống. Đồng thời, cũng giúp thầy cô tham khảo để soạn giáo án cho học sinh của mình theo chương trình mới. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com nhé:
Giải Toán 7 bài 28: Phép chia đa thức một biến sách Kết nối tri thức với cuộc sống
Giải Toán 7 Kết nối tri thức với cuộc sống trang 43 tập 2
Bài 7.30
Tính:
a) 8x5 : 4x3
b) 120x7 : (-24x5)
c) ![]() \(\dfrac{3}{4}{( - x)^3}:\dfrac{1}{8}x\)
\(\dfrac{3}{4}{( - x)^3}:\dfrac{1}{8}x\)
d) -3,72x 4 : (-4x 2)
Gợi ý đáp án:
a) 8x5 : 4x3 = (8 : 4) . (x5 : x3) = 2.x2
b) 120x7 : (-24x5) = [120 : (-24)] . (x7 : x5) = -5.x2
c) ![]() \(\dfrac{3}{4}{( - x)^3}:\dfrac{1}{8}x = \dfrac{{ - 3}}{4}{x^3}:\dfrac{1}{8}x = \left( {\dfrac{{ - 3}}{4}:\dfrac{1}{8}} \right).({x^3}:x) = - 6{x^2}\)
\(\dfrac{3}{4}{( - x)^3}:\dfrac{1}{8}x = \dfrac{{ - 3}}{4}{x^3}:\dfrac{1}{8}x = \left( {\dfrac{{ - 3}}{4}:\dfrac{1}{8}} \right).({x^3}:x) = - 6{x^2}\)
d) -3,72x 4 : (-4x 2 ) = [(-3,72) : (-4)] . (x 4 : x 2 ) = 0,93x 2
Bài 7.31
Thực hiện các phép chia đa thức sau:
a) ![]() \((-5x^3 + 15x^2 + 18x) : (-5x)\);
\((-5x^3 + 15x^2 + 18x) : (-5x)\);
b) ![]() \((-2x^5 – 4x^3 + 3x^2) : 2x^2\).
\((-2x^5 – 4x^3 + 3x^2) : 2x^2\).
Gợi ý đáp án:
a) ![]() \((-5x^3 + 15x^2 + 18x) : (-5x)\)
\((-5x^3 + 15x^2 + 18x) : (-5x)\)
![]() \(= (-5x^3) : (-5x) + 15x^2 : (-5x) + 18x : (-5x)\)
\(= (-5x^3) : (-5x) + 15x^2 : (-5x) + 18x : (-5x)\)
![]() \(= x^2 – 3x - \frac{18}{5}\)
\(= x^2 – 3x - \frac{18}{5}\)
b) ![]() \((-2x^5 – 4x^3 + 3x^2) : 2x^2\)
\((-2x^5 – 4x^3 + 3x^2) : 2x^2\)
![]() \(= (-2x^5 : 2x^2) + (-4x^3 : 2x^2) + (3x^2 : 2x^2)\)
\(= (-2x^5 : 2x^2) + (-4x^3 : 2x^2) + (3x^2 : 2x^2)\)
![]() \(= -x^3 – 2x - \frac{3}{2}\)
\(= -x^3 – 2x - \frac{3}{2}\)
Bài 7.32
Thực hiện các phép chia đa thức sau bằng cách đặt tính chia:
a) ![]() \((6x^3 – 2x^2 – 9x + 3) : (3x – 1)\);
\((6x^3 – 2x^2 – 9x + 3) : (3x – 1)\);
b) ![]() \((4x^4 + 14x^3 – 21x – 9) : (2x^2 – 3)\).
\((4x^4 + 14x^3 – 21x – 9) : (2x^2 – 3)\).
Gợi ý đáp án:
a) ![]() \((6x^3 – 2x^2 – 9x + 3) : (3x – 1)\);
\((6x^3 – 2x^2 – 9x + 3) : (3x – 1)\);
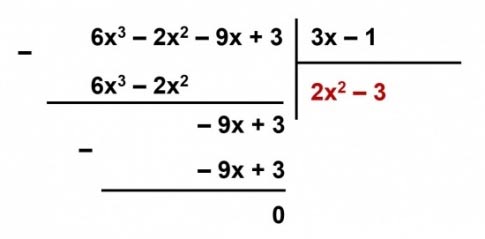
b) ![]() \((4x^4 + 14x^3 – 21x – 9) : (2x^2 – 3)\).
\((4x^4 + 14x^3 – 21x – 9) : (2x^2 – 3)\).
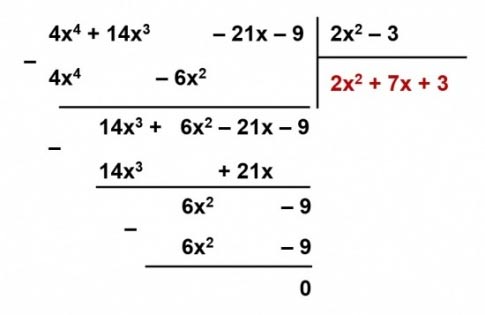
Bài 7.33
Thực hiện phép chia ![]() \(0,5x^5 + 3,2x^3 – 2x^2\) cho
\(0,5x^5 + 3,2x^3 – 2x^2\) cho ![]() \(0,25x^n\) trong mỗi trường hợp sau:
\(0,25x^n\) trong mỗi trường hợp sau:
a) n = 2;
b) n = 3.
Gợi ý đáp án:
a) n = 2
![]() \((0,5x^5 + 3,2x^3 – 2x^2) : 0,25x^2\)
\((0,5x^5 + 3,2x^3 – 2x^2) : 0,25x^2\)
![]() \(= (0,5x^5 : 0,25x^2) + (3,2x^3 : 0,25x^2) + (– 2x^2 : 0,25x^2)\)
\(= (0,5x^5 : 0,25x^2) + (3,2x^3 : 0,25x^2) + (– 2x^2 : 0,25x^2)\)
![]() \(= 2x^3 + 12,8x - 8\)
\(= 2x^3 + 12,8x - 8\)
b) n = 3
![]() \((0,5x^5 + 3,2x^3 – 2x^2) : 0,25x^3\)
\((0,5x^5 + 3,2x^3 – 2x^2) : 0,25x^3\)
![]() \(= (0,5x^5 : 0,25x^3) + (3,2x^3 : 0,25x^3) + (– 2x^2 : 0,25x^3)\)
\(= (0,5x^5 : 0,25x^3) + (3,2x^3 : 0,25x^3) + (– 2x^2 : 0,25x^3)\)
![]() \(= 2x^2 + 12,8 - \frac{8}{x}\)
\(= 2x^2 + 12,8 - \frac{8}{x}\)
Bài 7.34
Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng:
F(x) = G(x) . Q(x) + R(x).
a) ![]() \(F(x) = 6x^4 – 3x^3 + 15x^2 + 2x – 1; G(x) = 3x^2\).
\(F(x) = 6x^4 – 3x^3 + 15x^2 + 2x – 1; G(x) = 3x^2\).
b) ![]() \(F(x) = 12x^4 + 10x^3 – x – 3; G(x) = 3x^2 + x + 1\).
\(F(x) = 12x^4 + 10x^3 – x – 3; G(x) = 3x^2 + x + 1\).
Gợi ý đáp án:
a) ![]() \((6x^4 – 3x^3 + 15x^2 + 2x – 1) : 3x^2\)
\((6x^4 – 3x^3 + 15x^2 + 2x – 1) : 3x^2\)
* Cách 1: Phân tích ta thấy (2x – 1) có bậc nhỏ hơn ![]() \(3x^2\) nên (2x – 1) là số dư R(x) của đa thức trên.
\(3x^2\) nên (2x – 1) là số dư R(x) của đa thức trên.
![]() \(= (6x^4 – 3x^3 + 15x^2) : 3x^2\)
\(= (6x^4 – 3x^3 + 15x^2) : 3x^2\)
![]() \(= (6x^4 : 3x^2) + (– 3x^3 : 3x^2) + (15x^2 : 3x^2)\)
\(= (6x^4 : 3x^2) + (– 3x^3 : 3x^2) + (15x^2 : 3x^2)\)
![]() \(= 2x^2 – x + 5\)
\(= 2x^2 – x + 5\)
* Cách 2: Đặt tính:
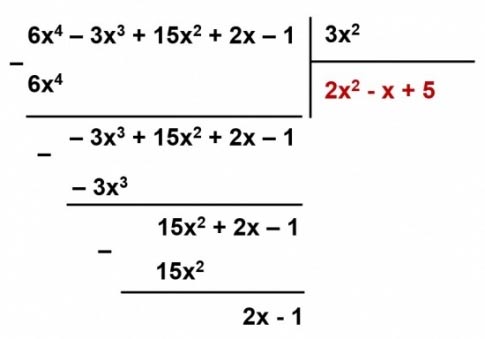
* Vậy: R(x) = 2x – 1
![]() \(Q(x) = 2x^2 – x + 5\)
\(Q(x) = 2x^2 – x + 5\)
![]() \(F(x) = 3x^2 . (2x^2 – x + 5) + 2x – 1\)
\(F(x) = 3x^2 . (2x^2 – x + 5) + 2x – 1\)
b) ![]() \((12x^4 + 10x^3 – x – 3) : (3x^2 + x + 1)\).
\((12x^4 + 10x^3 – x – 3) : (3x^2 + x + 1)\).
Đặt tính:
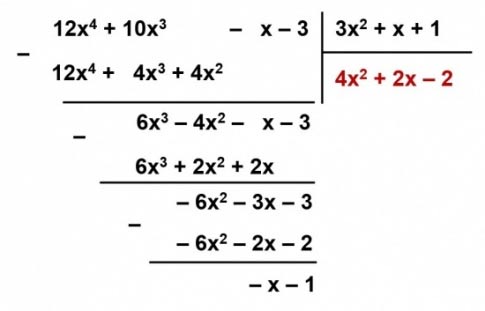
Vậy: R(x) = - x - 1
![]() \(Q(x) = 4x^2 + 2x - 2\)
\(Q(x) = 4x^2 + 2x - 2\)
![]() \(F(x) = (3x^2 + x + 1) . (4x^2 + 2x - 2) - x - 1\)
\(F(x) = (3x^2 + x + 1) . (4x^2 + 2x - 2) - x - 1\)
Bài 7.35
Bạn Tâm lúng túng khi muốn tìm thương và dư trong phép chia đa thức 21x – 4 cho ![]() \(3x^2\). Em có thể giúp bạn Tâm được không?
\(3x^2\). Em có thể giúp bạn Tâm được không?
Gợi ý đáp án:
Phân tích ta thấy (21x – 4) có bậc nhỏ hơn ![]() \(3x^2\) nên (21x – 4) của đa phép chia đa thức 21x – 4 cho
\(3x^2\) nên (21x – 4) của đa phép chia đa thức 21x – 4 cho ![]() \(3x^2\).
\(3x^2\).
* Vậy: Phép chia đa thức 21x – 4 cho ![]() \(3x^2\) có:
\(3x^2\) có:
- Thương là 0.
- Số dư là (21x – 4).
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:













 Toán 7 Kết nối tri thức
Toán 7 Kết nối tri thức
 Toán 7 Chân trời sáng tạo
Toán 7 Chân trời sáng tạo
 Toán 7 Cánh Diều
Toán 7 Cánh Diều
 Soạn Văn 7 Chân trời sáng tạo
Soạn Văn 7 Chân trời sáng tạo
 Soạn Văn 7 Cánh Diều
Soạn Văn 7 Cánh Diều
 Soạn Văn 7 Kết nối tri thức
Soạn Văn 7 Kết nối tri thức
 Tiếng Anh 7 Global Success
Tiếng Anh 7 Global Success
 Tiếng Anh 7 Explore English
Tiếng Anh 7 Explore English
 Tiếng Anh 7 - iLearn Smart World
Tiếng Anh 7 - iLearn Smart World









