Toán 7 Bài tập cuối chương III - Kết nối tri thức với cuộc sống Giải Toán lớp 7 trang 59 - Tập 1

Giải bài tập Toán lớp 7 Bài tập cuối chương III với lời giải chi tiết, rõ ràng theo khung chương trình SGK Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 59. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 7 chi tiết, còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của Bài tập cuối chương III: Góc và đường thẳng song song. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 7 Kết nối tri thức với cuộc sống trang 59 tập 1

Bài 3.32 trang 59 Toán 7 tập 1

Chứng minh rằng: Cho điểm A và đường thẳng d thì có duy nhất đường thẳng đi qua A và vuông góc với d, tức là nếu có hai đường thẳng đi qua A vuông góc với d thì chúng phải trùng nhau.

Hướng dẫn giải:

- Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại

- Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.

- Nếu một đường thẳng cắt hai đường thẳng song song thì:

• Hai góc so le trong bằng nhau.
• Hai góc đồng vị bằng nhau.

Gợi ý đáp án:

Giả sử có 2 đường thẳng a và a’ đi qua A và vuông góc với d.

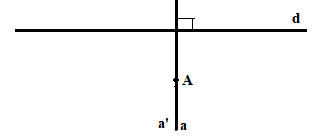
Vì \(a \bot d\), mà \(a’ \bot d\) nên a // a’ (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)

Mà \(A \in d\), \(A \in d’\)

\(\Rightarrow a \equiv a'\)

Vậy có duy nhất đường thẳng đi qua A và vuông góc với d

Bài 3.33 trang 59 Toán 7 tập 1

Vẽ ba đường thẳng phân biệt a, b, c sao cho a//b, b//c và hai đường thẳng phân biệt m, n cùng vuông góc với a. Hỏi trên hình có bao nhiêu cặp đường thẳng song song, có bao nhiêu cặp đường thẳng vuông góc?

Hướng dẫn giải:

- Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.

- Hai góc kề bù có số đo bằng 180⁰.

- Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.

- Khi Oz là tia phân giác của góc xOy thì \(\widehat {xOz} = \widehat {yOz} = \frac{1}{2}\widehat {xOy}\)

Gợi ý đáp án:

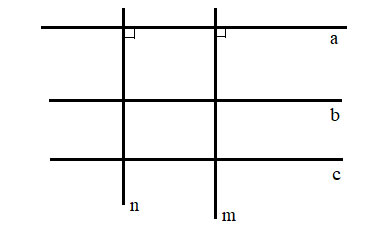
Ta có:

+) a // b, b // c nên a // c (Hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau)

+) \(m \bot a\); \(n \bot a\) nên m // n (Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)

Theo định lý “Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng vuông góc với đường thẳng kia", ta có:

+) a // b; \(a \bot n\) nên \(b \bot n\)

+) a // b; \(a \bot m\) nên \(b \bot m\)

+) a // c; \(a \bot n\) nên \(c \bot n\)

+) a // c; \(a \bot m\) nên \(c \bot m\)

Vậy các cặp đường thẳng song song là: a // b ; a // c ; b // c; m // n

Các cặp đường thẳng vuông góc là: \(b \bot n\); \(b \bot m\); \(c \bot n\); \(c \bot m\); \(a \bot n\); \(a \bot m\)

Bài 3.34 trang 59 Toán 7 tập 1

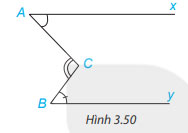
Cho Hình 3.50, trong đó hai tia Ax và By nằm trên hai đường thẳng song song. Chứng minh rằng \(\widehat C = \widehat A + \widehat B\)

Hướng dẫn giải:

- Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.

- Hai góc kề bù có số đo bằng 180⁰.

- Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.

- Khi Oz là tia phân giác của góc xOy thì \(\widehat {xOz} = \widehat {yOz} = \frac{1}{2}\widehat {xOy}\)

Gợi ý đáp án:

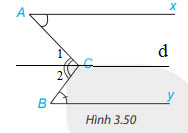
Qua C kẻ đường thẳng d song song với Ax

Vì Ax // By nên d // By

Vì d // Ax nên \(\widehat A = \widehat {{C_1}}\)(2 góc so le trong)

Vì d // By nên \(\widehat B = \widehat {{C_2}}\) (2 góc so le trong)

Mà \(\widehat C = \widehat {{C_1}} + \widehat {{C_2}}\)

Vậy \(\widehat C = \widehat A + \widehat B(đpcm)\)

Bài 3.35 trang 59 Toán 7 tập 1

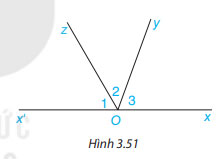
Cho Hình 3.51, trong đó Ox và Ox’ là hai tia đối nhau

a) Tính tổng số đo ba góc O1, O2, O3 .

Gợi ý:\(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}\), trong đó \(\widehat {{O_1}} + \widehat {{O_2}} = \widehat {x'Oy}\)

b) Cho \(\widehat {{O_1}} = 60^\circ ,\widehat {{O_2}} = 70^\circ\). Tính \(\widehat {{O_2}}\)

Hướng dẫn giải:

- Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.

- Hai góc kề bù có số đo bằng 180⁰.

- Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.

- Khi Oz là tia phân giác của góc xOy thì \(\widehat {xOz} = \widehat {yOz} = \frac{1}{2}\widehat {xOy}\)

Gợi ý đáp án:

a) Ta có: \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}=\widehat {x'Oy} + \widehat {{O_3}}\), mà \(\widehat {x'Oy} + \widehat {{O_3}}= 180^\circ\) (2 góc kề bù)

Vậy \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ\)

b) Vì \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ\)

\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {{O_2}} + 70^\circ = 180^\circ \\ \Rightarrow \widehat {{O_2}} = 180^\circ - 60^\circ - 70^\circ = 50^\circ \end{array}\)

Vậy \(\widehat {{O_2}} = 50^\circ\)

Bài 3.36 trang 59 Toán 7 tập 1

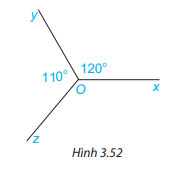
Cho Hình 3.52, biết \(\widehat {xOy} = 120^\circ ,\widehat {yOz} = 110^\circ\). Tính số đo góc zOx.

Gợi ý: Kẻ thêm tia đối của tia Oy

Hướng dẫn giải:

- Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.

- Hai góc kề bù có số đo bằng 180⁰.

- Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.

- Khi Oz là tia phân giác của góc xOy thì \(\widehat {xOz} = \widehat {yOz} = \frac{1}{2}\widehat {xOy}\)

Gợi ý đáp án:

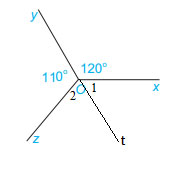
Kẻ Ot là tia đối của tia Oy.

Ta được:

+) \(\widehat {{O_1}} + \widehat {xOy} = 180^\circ\) (2 góc kề bù)

\(\begin{array}{l} \Rightarrow \widehat {{O_1}} + 120^\circ = 180^\circ \\ \Rightarrow \widehat {{O_1}} = 180^\circ - 120^\circ = 60^\circ \end{array}\)

+) \(\widehat {{O_2}} + \widehat {yOz} = 180^\circ\) (2 góc kề bù)

Vì Ot nằm giữa 2 tia Ox và Oz nên \(\widehat {xOz} = \widehat {{O_1}} + \widehat {{O_2}} = 60^\circ + 70^\circ = 130^\circ\)

Vậy \(\widehat {zOx} = 130^\circ\)