Toán 7 Luyện tập chung trang 14 Giải Toán lớp 7 trang 14, 15 sách Kết nối tri thức - Tập 1

Bài trước

Mục lục

Bài sau

Giải bài tập Toán lớp 7 Luyện tập chung với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 14, 15. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 7 chi tiết phần bài tập, đồng thời còn giúp các em hệ thống lại toàn bộ kiến thức lý thuyết trọng tâm của Luyện tập chung Chương I: Số hữu tỉ. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 7 bài Luyện tập chung trang 14 Kết nối tri thức với cuộc sống

Giải Toán 7 Kết nối tri thức với cuộc sống trang 14, 15 tập 1

Bài 1.12 trang 14 Toán 7 tập 1

So sánh:

a) $\frac{{123}}{7}$ $\frac{{123}}{7}$ và 17,75

b) $- \frac{{65}}{9}$ $- \frac{{65}}{9}$ và -7,125

Hướng dẫn giải

- Với hai số hữu tỉ a, b bất kì, ta luôn có hoặc a = b hoặc a b.

Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).

- Trên trục số nếu a < b thì điểm a nằm trước điểm b.

Gợi ý đáp án:

a) $\frac{{123}}{7}$ $\frac{{123}}{7}$ và 17,75

Ta có:

$\begin{matrix} 17,75 = \dfrac{{1775}}{{100}} = \dfrac{{71}}{4} = \dfrac{{71.7}}{{4.7}} = \dfrac{{497}}{{28}} \hfill \\ \dfrac{{123}}{7} = \dfrac{{123.4}}{{7.4}} = \dfrac{{492}}{{28}} \hfill \\ \end{matrix}$ $\begin{matrix} 17,75 = \dfrac{{1775}}{{100}} = \dfrac{{71}}{4} = \dfrac{{71.7}}{{4.7}} = \dfrac{{497}}{{28}} \hfill \\ \dfrac{{123}}{7} = \dfrac{{123.4}}{{7.4}} = \dfrac{{492}}{{28}} \hfill \\ \end{matrix}$

Do 497 > 492 => $\frac{{497}}{{28}} > \frac{{492}}{{28}}$ $\frac{{497}}{{28}} > \frac{{492}}{{28}}$

Vậy $17,75 > \frac{{123}}{7}$ $17,75 > \frac{{123}}{7}$

b) $- \frac{{65}}{9}$ $- \frac{{65}}{9}$ và -7,125

Ta có:

$\begin{matrix} - 7,125 = \dfrac{{ - 7125}}{{1000}} = - \dfrac{{57}}{8} = - \dfrac{{513}}{{72}} \hfill \\ - \dfrac{{65}}{9} = - \dfrac{{65.8}}{{9.8}} = - \dfrac{{520}}{{72}} \hfill \\ \end{matrix}$ $\begin{matrix} - 7,125 = \dfrac{{ - 7125}}{{1000}} = - \dfrac{{57}}{8} = - \dfrac{{513}}{{72}} \hfill \\ - \dfrac{{65}}{9} = - \dfrac{{65.8}}{{9.8}} = - \dfrac{{520}}{{72}} \hfill \\ \end{matrix}$

Do 520 > 513 => -520 < -513

=> $- \frac{{520}}{{72}} < - \frac{{513}}{{72}}$ $- \frac{{520}}{{72}} < - \frac{{513}}{{72}}$

Vậy $- \frac{{65}}{9} < - 7,125$ $- \frac{{65}}{9} < - 7,125$

Bài 1.13 trang 15 Toán 7 tập 1

Bảng sau cho biết các điểm đông đặc và điểm sôi của sáu nguyên tố được gọi là khí hiếm.

Khí hiếm	Điểm đông đặc (^oC)	Điểm sôi (^oC)
Argon (A – gon)	–189,2	–185,7
Helium (Hê – li)	–272,2	–268,6
Neon (Nê – on)	–248,67	–245,72
Krypton (Kríp – tôn)	–156,6	–152,3
Radon (Ra – đôn)	–71,0	–61,8
Xenon (Xê – nôn)	–111,9	–107,1

(Theo britannica.com)

a) Khí hiếm nào có điểm đông đặc nhỏ hơn điểm đông đặc của Krypton?

b) Khí hiếm nào có điểm sôi lớn hơn điểm sôi của Argon?

c) Hãy sắp xếp các khí hiếm theo thứ tự điểm đông đặc tăng dần;

d) Hãy sắp xếp các khí hiếm theo thứ tự điểm sôi giảm dần.

Hướng dẫn giải

- Với hai số hữu tỉ a, b bất kì, ta luôn có hoặc a = b hoặc a b.

Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).

- Trên trục số nếu a < b thì điểm a nằm trước điểm b.

Gợi ý đáp án:

a) Ta có:

–156,6 > –189,2 > –248,67 > –272,2

=> Khí hiếm có điểm đông đặc nhỏ hơn điểm đông đặc của Krypton là: Argon, Neon, Helium.

Vậy khí hiếm có điểm đông đặc nhỏ hơn điểm đông đặc của Krypton là: Argon, Neon, Helium.

b) Ta có:

–61,8 > –107,1 > –152,3 > –185,7

=> Khí hiếm có điểm sôi lớn hơn điểm sôi của Argon là: Radon, Xenon, Krypton.

Vậy khí hiếm có điểm sôi lớn hơn điểm sôi của Argon là: Radon, Xenon, Krypton.

c) Ta có:

–272,2 < –248,67 < –189,2 < –156,6 < –111,9 < –71,0

=> Các khí hiếm sắp xếp theo thứ tự đông đặc tăng dần là: Helium, Neon, Argon, Krypton, Xenon, Radon.

Vậy khí hiếm sắp xếp theo thứ tự đông đặc tăng dần là: Helium, Neon, Argon, Krypton, Xenon, Radon.

d) Ta có:

–61,8 > –107,1 > –152,3 > –185,7 > –245,72 > –268,6

=> Các khí hiếm sắp xếp theo thứ tự điểm sôi giảm dần là: Radon, Xenon, Krypton, Argon, Neon, Helium.

Vậy các khí hiếm sắp xếp theo thứ tự điểm sôi giảm dần là: Radon, Xenon, Krypton, Argon, Neon, Helium.

Bài 1.14 trang 15 Toán 7 tập 1

Theo Đài khí tượng thủy văn tỉnh Lào Cai, ngày 10 – 01 – 2021, nhiệt độ thấp nhất tại thị xã Sa Pa là – 0,7⁰C; nhiệt độ tại thành phố Lào Cai là 9,6⁰C. Hỏi nhiệt độ tại thành phố Lào Cai cao hơn nhiệt độ tại thị xã Sa Pa bao nhiêu độ C?

(Theo vietnamplus.vn)

Hướng dẫn giải

- Với hai số hữu tỉ a, b bất kì, ta luôn có hoặc a = b hoặc a b.

Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).

- Trên trục số nếu a < b thì điểm a nằm trước điểm b.

Gợi ý đáp án:

Nhiệt độ tại thành phố Lào Cai cao hơn nhiệt độ tại thị xã Sa Pa là:

9,6 – (– 0,7) = 9,6 + 0,7 = 10,3 (^oC)

Vậy nhiệt độ tại thành phố Lào Cai cao hơn 10,3 ^oC so với nhiệt độ tại thị xã Sa Pa.

Bài 1.15 trang 15 Toán 7 tập 1

Thay mỗi dấu “?” bằng số thích hợp để hoàn thiện sơ đồ Hình 1.11, biết số trong mỗi ô ở hàng trên bằng tích của hai số trong hai ô kề nó ở hàng dưới.

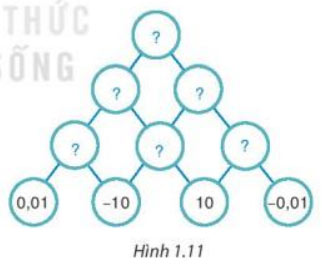
Hình 1.11

Hướng dẫn giải

- Tính chất phân phối của phép nhân đối với phép cộng:

a.b + a.c = a.(b + c)

- Ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.

- Ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

Gợi ý đáp án:

Chú thích bài toán bằng hình vẽ sau:

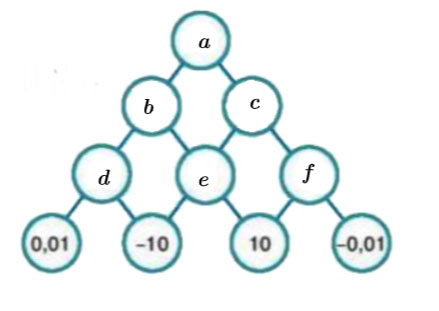
Hình 1.11

Theo bài ra ta có: Số trong mỗi ô ở hàng trên bằng tích của hai số trong hai ô kề nó ở hàng dưới

Áp dụng công thức ta có:

d = 0,01 . (-10) = -0,1

e = -10 . 10 = -100

f = -0,01 . 10 = -0,1

b = d . e = -0,1 . -100 = 10

c = e . f = -100 . -0,1 = 10

a = b . c = 10 . 10 = 100

Hoàn thành cây sơ đồ như sau:

Hình 1.11

Bài 1.16 trang 15 Toán 7 tập 1

Tính giá trị của các biểu thức sau:

a) $A = \left( {2 - \frac{1}{2} - \frac{1}{8}} \right):\left( {1 - \frac{3}{2} - \frac{3}{4}} \right)$ $A = \left( {2 - \frac{1}{2} - \frac{1}{8}} \right):\left( {1 - \frac{3}{2} - \frac{3}{4}} \right)$

b) $B = 5 - \dfrac{{1 + \dfrac{1}{3}}}{{1 - \dfrac{1}{3}}}$ $B = 5 - \dfrac{{1 + \dfrac{1}{3}}}{{1 - \dfrac{1}{3}}}$

Hướng dẫn giải

- Tính chất phân phối của phép nhân đối với phép cộng:

a.b + a.c = a.(b + c)

- Ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.

- Ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

Gợi ý đáp án:

Thực hiện phép tính ta có:

$A = \left( {\frac{{16}}{8} - \frac{4}{8} - \frac{1}{8}} \right):\left( {\frac{4}{4} - \frac{6}{4} - \frac{3}{4}} \right)$ $A = \left( {\frac{{16}}{8} - \frac{4}{8} - \frac{1}{8}} \right):\left( {\frac{4}{4} - \frac{6}{4} - \frac{3}{4}} \right)$

$A = \frac{{11}}{8}:\frac{{ - 5}}{4}$ $A = \frac{{11}}{8}:\frac{{ - 5}}{4}$

$A = \frac{{11}}{8}.\frac{4}{{ - 5}} = \frac{{11}}{{ - 10}}$ $A = \frac{{11}}{8}.\frac{4}{{ - 5}} = \frac{{11}}{{ - 10}}$

b) $B = 5 - \dfrac{{1 + \dfrac{1}{3}}}{{1 - \dfrac{1}{3}}}$ $B = 5 - \dfrac{{1 + \dfrac{1}{3}}}{{1 - \dfrac{1}{3}}}$

$B = 5 - \dfrac{{\dfrac{3}{3} + \dfrac{1}{3}}}{{\dfrac{3}{3} - \dfrac{1}{3}}}$ $B = 5 - \dfrac{{\dfrac{3}{3} + \dfrac{1}{3}}}{{\dfrac{3}{3} - \dfrac{1}{3}}}$

$B = 5 - \frac{4}{3}:\frac{2}{3}$ $B = 5 - \frac{4}{3}:\frac{2}{3}$

$B = 5 - \frac{4}{3}.\frac{3}{2}$ $B = 5 - \frac{4}{3}.\frac{3}{2}$

$B = 5 - 2 = 3$

Bài 1.17 trang 15 Toán 7 tập 1

Tính một cách hợp lí

$1,2.\frac{{15}}{4} + \frac{{16}}{7}.\frac{{ - 85}}{8} - 1,2.5\frac{3}{4} - \frac{{16}}{7}.\frac{{ - 71}}{8}$ $1,2.\frac{{15}}{4} + \frac{{16}}{7}.\frac{{ - 85}}{8} - 1,2.5\frac{3}{4} - \frac{{16}}{7}.\frac{{ - 71}}{8}$

Hướng dẫn giải

- Tính chất phân phối của phép nhân đối với phép cộng:

a.b + a.c = a.(b + c)

- Ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.

- Ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

Gợi ý đáp án:

Thực hiện phép tính như sau:

$= 1,2.\frac{{15}}{4} - 1,2.\frac{{23}}{4} + \frac{{16}}{7}.\frac{{ - 85}}{8} - \frac{{16}}{7}.\frac{{ - 71}}{8}$ $= 1,2.\frac{{15}}{4} - 1,2.\frac{{23}}{4} + \frac{{16}}{7}.\frac{{ - 85}}{8} - \frac{{16}}{7}.\frac{{ - 71}}{8}$

$= 1,2.\left( {\frac{{15}}{4} - \frac{{23}}{4}} \right) + \frac{{16}}{7}.\left( {\frac{{ - 85}}{8} - \frac{{ - 71}}{8}} \right)$ $= 1,2.\left( {\frac{{15}}{4} - \frac{{23}}{4}} \right) + \frac{{16}}{7}.\left( {\frac{{ - 85}}{8} - \frac{{ - 71}}{8}} \right)$

$= 1,2.\frac{{ - 8}}{4} + \frac{{16}}{7}.\frac{{ - 14}}{8}$ $= 1,2.\frac{{ - 8}}{4} + \frac{{16}}{7}.\frac{{ - 14}}{8}$

$= - 2,4 + \left( { - 4} \right) = - 6,4$ $= - 2,4 + \left( { - 4} \right) = - 6,4$

Lý thuyết Toán 7 Luyện tập chung trang 14

1. Số hữu tỉ

- Số hữu tỉ là số viết dưới dạng phân số $\frac{a}{b}$ $\frac{a}{b}$ với $a,b \in \mathbb{Z},b \ne 0$ $a,b \in \mathbb{Z},b \ne 0$.

- Tập hợp các số hữu tỉ được kí hiệu là $\mathbb{Q}$ $\mathbb{Q}$

Ví dụ: -3; -1,75, $4\frac{1}{5}$ $4\frac{1}{5}$, … là các số hữu tỉ.

- Số nguyên a bất kì là một số hữu tỉ vì số nguyên a có thể viết dưới dạng $\frac{a}{1}$ $\frac{a}{1}$

Ví dụ: Ta có 1; -3; 0 là các số hữu tỉ.

Ta có:

$\begin{matrix} 1 = \dfrac{1}{1} \Rightarrow 1 \in \mathbb{Q} \hfill \\ - 3 = \dfrac{{ - 3}}{1} \Rightarrow - 3 \in \mathbb{Q} \hfill \\ 0 = \dfrac{0}{1} \Rightarrow 0 \in \mathbb{Q} \hfill \\ \end{matrix}$ $\begin{matrix} 1 = \dfrac{1}{1} \Rightarrow 1 \in \mathbb{Q} \hfill \\ - 3 = \dfrac{{ - 3}}{1} \Rightarrow - 3 \in \mathbb{Q} \hfill \\ 0 = \dfrac{0}{1} \Rightarrow 0 \in \mathbb{Q} \hfill \\ \end{matrix}$

Nhận xét: $\mathbb{Z} = \left\{ {0; \pm 1; \pm 2;...} \right\}$ $\mathbb{Z} = \left\{ {0; \pm 1; \pm 2;...} \right\}$ đều là số hữu tỉ

Từ đó => Biểu đồ Ven biểu thị mối quan hệ các tập hợp số:

2. Biểu diễn số hữu tỉ trên trục số

- Để biểu diễn số hữu tỉ trên trục số ta làm theo các ước sau:

Bước 1: Viết số hữu tỉ dưới dạng phân số $\frac{a}{b}$ $\frac{a}{b}$

Bước 2: Chia đoạn thẳng đơn vị thành b phần bằng nhau ta được đoạn đơn vị mới là $\frac{1}{b}$ $\frac{1}{b}$ đơn vị cũ.

Bước 3: Số hữu tỉ $\frac{a}{b}$ $\frac{a}{b}$ được biểu diễn bằng điểm A cách điểm 0 một đoạn bằng a đơn vị mới.

+ A nằm bên trái điểm 0 nếu là số âm.

+ A nằm bên phải điểm 0 nếu là số dương.

3. So sánh hai số hữu tỉ

- Với 2 số hữu tỉ bất kì x, y ta luôn có hoặc x = y hoặc x < y hoặc x > y.

- Để so sánh hai số hữu tỉ x, y ta làm như sau:

+) Viết x, y dưới dạng 2 phân số cùng mẫu dương: $x = \frac{a}{m};{\mkern 1mu} y = \frac{b}{m};{\mkern 1mu} \left( {m > 0} \right)$ $x = \frac{a}{m};{\mkern 1mu} y = \frac{b}{m};{\mkern 1mu} \left( {m > 0} \right)$

+) So sánh tử số là các số nguyên a, b:

$\begin{array}{*{20}{l}} {a b \Rightarrow x > y} \\ {a = b \Rightarrow x = y} \end{array}$ $\begin{array}{*{20}{l}} {a b \Rightarrow x > y} \\ {a = b \Rightarrow x = y} \end{array}$

4. Quy tắc cộng, trừ hai số hữu tỉ

Ta có thể cộng, trừ hai số hữu tỉ x, y bằng cách viết chúng dưới dạng hai phân số rồi áp dụng quy tắc cộng, trừ phân số

Với $x = \frac{p}{m};y = \frac{q}{m};\left( {p,q,m \in \mathbb{Z},m > 0} \right)$ $x = \frac{p}{m};y = \frac{q}{m};\left( {p,q,m \in \mathbb{Z},m > 0} \right)$ ta có:

$x + y = \frac{p}{m} + \frac{q}{m} = \frac{{p + q}}{m}$ $x + y = \frac{p}{m} + \frac{q}{m} = \frac{{p + q}}{m}$

$x - y = \frac{p}{m} - \frac{q}{m} = \frac{{p - q}}{m}$ $x - y = \frac{p}{m} - \frac{q}{m} = \frac{{p - q}}{m}$

Chia sẻ bởi: