Toán 7 Bài 7: Tập hợp các số thực Giải Toán lớp 7 trang 33 - Tập 1 sách Kết nối tri thức với cuộc sống

Tải về

Giải Toán lớp 7 bài 7: Tập hợp các số thực bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 33, 34, 35, 36.

Lời giải Toán 7 Bài 7 Kết nối tri thức trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 7, từ đó học tốt môn Toán lớp 7 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 7 Chương II - Số thực. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 7 bài 7: Tập hợp các số thực sách Kết nối tri thức với cuộc sống

Giải Toán 7 Kết nối tri thức với cuộc sống tập 1 bài 7 - Luyện tập

Luyện tập 1

a) Trong các cách viết $\sqrt 2 \in \mathbb{Q};15 \in \mathbb{R}$ $\sqrt 2 \in \mathbb{Q};15 \in \mathbb{R}$, cách viết nào đúng?

b) Viết số đối của các số: 5,08(299); $\sqrt 5$ $\sqrt 5$

Gợi ý đáp án:

a) Ta có: $\sqrt 2$ $\sqrt 2$ là số vô tỉ

=> $\sqrt 2 \in \mathbb{Q}$ $\sqrt 2 \in \mathbb{Q}$ là cách viết sai

15 là số hữu tỉ => 15 thuộc tập số thực

=> $15 \in \mathbb{R}$ $15 \in \mathbb{R}$ là cách viết đúng.

b) Số đối của các số 5,08(299) là số -5,08(299)

Số đối của các số $\sqrt 5$ $\sqrt 5$ là số $- \sqrt 5$ $- \sqrt 5$

Luyện tập 2

Cho biết nếu một tam giác vuông có hai cạnh góc vuông bằng 1 và 3 thì cạnh huyền của tam giác bằng $\sqrt {10}$ $\sqrt {10}$ . Em hãy vẽ điểm biểu diễn số $- \sqrt {10}$ $- \sqrt {10}$ trên trục số.

Gợi ý đáp án:

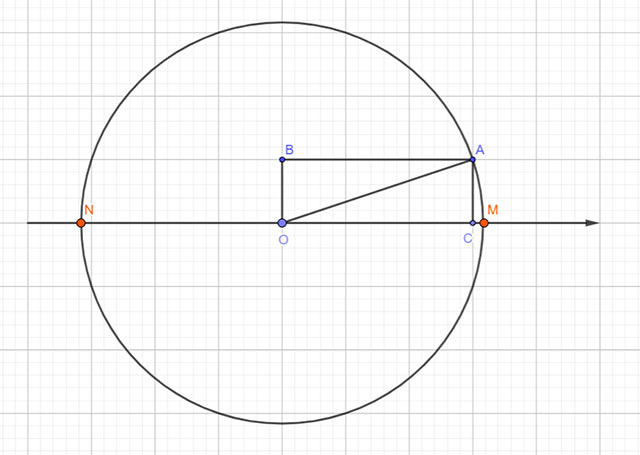
Bước 1: Vẽ hình chữ nhật OABC có hai cạnh bằng 3 và 1.

Khi đó ta được $OA = \sqrt {10}$ $OA = \sqrt {10}$

Bước 2: Vẽ đường tròn tâm O, bán kính OA cắt tia Ox tại hai điểm M

=> $OM = OA = \sqrt {10}$ $OM = OA = \sqrt {10}$

Trên tia đối của tia Ox lấy điểm N sao cho ON = OM

=> $OM = ON = \sqrt {10}$ $OM = ON = \sqrt {10}$

=> Điểm N biểu diễn số $- \sqrt {10}$ $- \sqrt {10}$

Hình vẽ minh họa:

Hình vẽ minh họa

Luyện tập 3

So sánh:

a) 1,313233 … và 1,(32)

b) $\sqrt 5$ $\sqrt 5$ và 2,36 (có thể dùng máy tính cầm tay để tính $\sqrt 5$ $\sqrt 5$)

Gợi ý đáp án:

a) Ta có:

1,(32) = 1,323232 ….

Mà 1,313233 … < 1,323232 ….

=> 1,313233 … < 1,(32)

c) Ta có:

Sử dụng máy tính cầm tay tính $\sqrt 5$ $\sqrt 5$ ta được kết quả:

$\sqrt 5 \approx 2,24$ $\sqrt 5 \approx 2,24$

Mà 2,24 < 2,26

=> $\sqrt 5 < 2,26$ $\sqrt 5 < 2,26$

Luyện tập 4

Tính:

a) |-2,3|

b) $\left| {\frac{7}{5}} \right|$ $\left| {\frac{7}{5}} \right|$

c) |-11|

d) $\left| { - \sqrt 8 } \right|$ $\left| { - \sqrt 8 } \right|$

Gợi ý đáp án:

a) |-2,3| = 2,3

b) $\left| {\frac{7}{5}} \right| = \frac{7}{5}$ $\left| {\frac{7}{5}} \right| = \frac{7}{5}$

c) |-11| = 11

d) $\left| { - \sqrt 8 } \right| = \sqrt 8$ $\left| { - \sqrt 8 } \right| = \sqrt 8$

Giải Toán 7 Kết nối tri thức với cuộc sống trang 36 tập 1

Bài 2.13

Xét tập hợp $A = \left\{ {7,1; - 2,(61);0;5,14;\frac{4}{7};\sqrt {15} ; - \sqrt {81} } \right\}$ $A = \left\{ {7,1; - 2,(61);0;5,14;\frac{4}{7};\sqrt {15} ; - \sqrt {81} } \right\}$. Bằng cách liệt kê phần tử, hãy viết tập hợp B gồm các số hữu tỉ thuộc tập A và tập hợp C gồm các số vô tỉ

Gợi ý đáp án:

$B = \left\{ {7,1; - 2,(61);0;5,14;\frac{4}{7}; - \sqrt {81} } \right\}$ $B = \left\{ {7,1; - 2,(61);0;5,14;\frac{4}{7}; - \sqrt {81} } \right\}$

$C = \left\{ {\sqrt {15} } \right\}$ $C = \left\{ {\sqrt {15} } \right\}$

Chú ý:

Số $- \sqrt {81}$ $- \sqrt {81}$là số hữu tỉ vì $- \sqrt {81} =-9$ $- \sqrt {81} =-9$

Bài 2.14

Gọi A’ là tập hợp các số đối của các số thuộc tập A trong bài tập 2.13. Liệt kê các phần tử của A’

Gợi ý đáp án:

Số đối của số 7,1 là -7,1

Số đối của số -2,(61) là 2,(61)

Số đối của số 0 là 0

Số đối của số 5,14 là -5,14

Số đối của số $\frac{4}{7}$ $\frac{4}{7}$ là $- \frac{4}{7}$ $- \frac{4}{7}$

Số đối của số $\sqrt {15}$ $\sqrt {15}$ là $- \sqrt {15}$ $- \sqrt {15}$

Số đối của số $- \sqrt {81} = \sqrt {81}$ $- \sqrt {81} = \sqrt {81}$

Bài 2.15

Mũi tên màu xanh trong mỗi hình sau chỉ số thực nào?

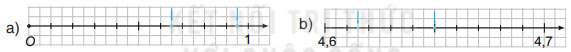
Bài 2.15

Gợi ý đáp án:

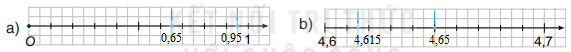
Bài 2.15

Bài 2.16

Tính:

$a)\left| { - 3,5} \right|;$ $a)\left| { - 3,5} \right|;$ $b)\left| {\frac{{ - 4}}{9}} \right|;$ $b)\left| {\frac{{ - 4}}{9}} \right|;$ $c)\left| 0 \right|;$ $c)\left| 0 \right|;$ $d)\left| {2,0(3)} \right|.$ $d)\left| {2,0(3)} \right|.$

Gợi ý đáp án:

$\begin{array}{l}a)\left| { - 3,5} \right| = 3,5;\\b)\left| {\frac{{ - 4}}{9}} \right| = \frac{4}{9};\\c)\left| 0 \right| = 0;\\d)\left| {2,0(3)} \right| = 2,0(3)\end{array}$ $\begin{array}{l}a)\left| { - 3,5} \right| = 3,5;\\b)\left| {\frac{{ - 4}}{9}} \right| = \frac{4}{9};\\c)\left| 0 \right| = 0;\\d)\left| {2,0(3)} \right| = 2,0(3)\end{array}$

Chú ý:

Nếu $a \ge 0$ $a \ge 0$ thì $\left| a \right| = a$ $\left| a \right| = a$

Nếu a < 0 thì $\left| a \right| = - a$ $\left| a \right| = - a$

Bài 2.17

Xác định dấu và giá trị tuyệt đối của mỗi số sau:

a) a = 1,25;

b) b = - 4,1;

c) c = - 1,414213562....

Gợi ý đáp án:

a) a = 1,25 có dấu dương, $\left| a \right| = \left| {1,25} \right| = 1,25$ $\left| a \right| = \left| {1,25} \right| = 1,25$

b) b = - 4,1 có dấu âm, $\left| b \right| = \left| { - 4,1} \right| = 4,1$ $\left| b \right| = \left| { - 4,1} \right| = 4,1$

c) c = - 1,414213562.... có dấu âm, $\left| c \right| = \left| { - 1,414213562....} \right| = 1,414213562....$ $\left| c \right| = \left| { - 1,414213562....} \right| = 1,414213562....$

Bài 2.18

Tìm tất cả các số thực x thỏa mãn điều kiện $\left| x \right| = 2,5$ $\left| x \right| = 2,5$

Gợi ý đáp án:

Các số thực x thỏa mãn điều kiện $\left| x \right| = 2,5$ $\left| x \right| = 2,5$ là các số thực có khoảng cách từ số đó đến gốc tọa độ O là 2,5.

Đó là 2 số -2,5 và 2,5 nằm về 2 phía so với gốc O và cách gốc O một khoảng 2,5 đơn vị.

Chú ý: Có 2 số thực thỏa mãn giá trị tuyệt đối của nó bằng một số dương cho trước.

Chia sẻ bởi:

Lê Thị tuyết Mai

Tải về

Bài trước

Bài sau

Liên kết tải về

Toán 7 Bài 7: Tập hợp các số thực 221,3 KB

Tải về

Tìm thêm: Kết nối tri thức với cuộc sống Kết nối tri thức với cuộc sống Lớp 7

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!