Toán 7 Bài tập cuối chương IX - Kết nối tri thức với cuộc sống Giải Toán lớp 7 trang 84 - Tập 2

Toán 7 Bài tập cuối chương IX giúp các em học sinh lớp 7 tham khảo, biết cách giải toàn bộ các bài tập SGK Toán 7 Tập 2 trang 84 sách Kết nối tri thức với cuộc sống.

Với lời giải chi tiết bài tập Toán 7 này, còn giúp các em học sinh ôn tập và củng cố các dạng bài tập trong Chương 9 - Quan hệ giữa các yếu tố trong một tam giác, cũng như rèn luyện kỹ năng giải môn Toán thật tốt. Nhờ đó, sẽ đạt kết quả cao trong các bài kiểm tra, bài thi sắp tới. Chi tiết mời các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 7 Kết nối tri thức với cuộc sống trang 84 tập 2

Bài 9.36

Cho tam giác ABC có \(\widehat{BAC}\) là một góc tù. Lấy điểm D nằm giữa A và B, lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.

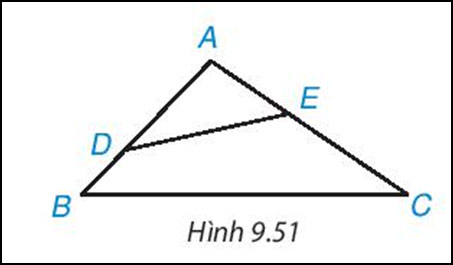
Gợi ý đáp án:

Vì \(\widehat{BAC}\) là góc tù nên \(\widehat{ADE} ,\widehat{AED}\) là các góc nhọn

\(=> \widehat{DEC}\) là góc tù.

=>DC>DE (quan hệ giữa góc và cạnh đối diện trong tam giác DEC). (1)

Xét tam giác ADC có:

\(\widehat{DAC}\) là góc tù nên \(\widehat{ADC} ,\widehat{ACD}\) là các góc nhọn

\(=> \widehat{BDC}\) là góc tù.

=>BC>DC (quan hệ giữa góc và cạnh đối diện trong tam giác BDC) (2)

- Từ (1) và (2) suy ra: BC>DE

Bài 9.37

Cho tam giác ABC (AB> AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa B D và C, C nằm giữa B và E, BD = BA, CE= CA ( H.9.52)

a) So sánh \(\widehat{ADE}\) và \(\widehat{AED}\)

b) So sánh các đoạn thẳng AD và AE

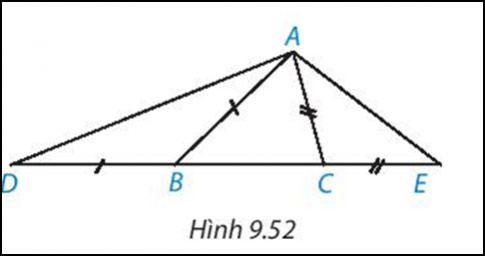
Gợi ý đáp án:

a) \(AB > AC => \widehat{ABC} < \widehat{ACB}\)(quan hệ giữa góc và cạnh đối diện trong tam giác ABC)

\(\widehat{ABD} + \widehat{ABC} = 180° => \widehat{ABC} = 180°- \widehat{ABD}\)

\(\widehat{ACE} + \widehat{ACB} = 180° => \widehat{ACB} = 180°- \widehat{ACE}\)

\(=> 180°- \widehat{ABD} < 180°- \widehat{ACE}\)

\(=> \widehat{ACE} < \widehat{ABD}\)

Tam giác ABD cân tại \(B ( BD= BA) => \widehat{ABD}= 180°- 2\widehat{ADB}\)

Tam giác ACE cân tại \(C ( CE= CA) => \widehat{ACE}= 180°- 2\widehat{AEC}\)

\(=> 180°- 2\widehat{ADB} > 180°- 2\widehat{AEC}\)

\(=> \widehat{ADB} < \widehat{AEC}\)

b) Xét tam giác ADE ta có: \(\widehat{ADB} < \widehat{AEC}\)

=> AD > AE

Bài 9.38

Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng

a) \(AI < \frac{1}{2} (AB + AC)\)

b) \(AM < \frac{1}{2} (AB + AC)\)

Gợi ý đáp án:

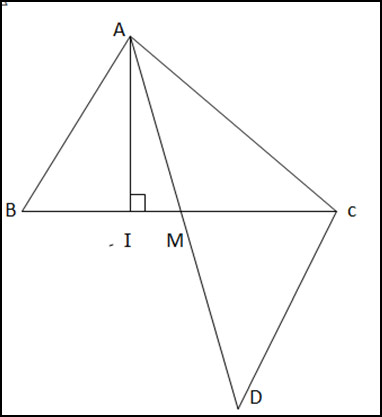
a) AI là đường cao từ A xuống đoạn thẳng BC=> AI là khoảng cách từ A đến BC => AI ngắn nhất

=> AI < AB và AI < AC

Cộng 2 vế với nhau ta có: 2 AI < AB + AC

\(=> AI <\frac{1}{2} (AB + AC)\)

b) Lấy D sao cho M là trung điểm của AD

Xét ∆ ABM và ∆ DCM có

AM = DM (M là trung điểm của AD)

BM=CM (M là trung điểm của BC)

\(\widehat{AMB} = \widehat{CMD}\) (2 góc đối đỉnh)

=> ∆ ABM = ∆ DCM

=>AB = CD

Xét ∆ ADC ta có: AD < AC + CD

=> 2AM < AC + AB

\(=> AM < \frac{1}{2} (AB + AC)\)

Bài 9.39

Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD = 2 DC. Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.53). Chứng minh rằng tam giác ABE cân tại A.

Gợi ý D là trọng tâm của tam giác ABE, tam giác này có đường phân giác AD đồng thời là trung tuyến.

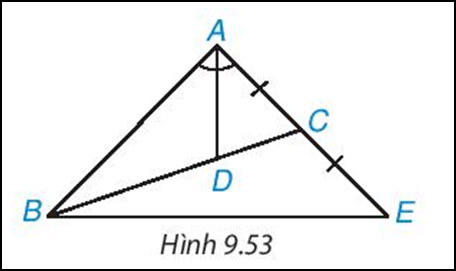
Gợi ý đáp án:

C là trung điểm của AE => BC là trung tuyến của tam giác ABE (1)

D thuộc BC, BD= 2DC

\(=> BC= BD + DC = 2DC + DC = 3DC => DC = \frac{1}{3} BC (2)\)

Từ (1) và (2) => D là trọng tâm của tam giác ABE

=> AD là đường trung tuyến ứng với BE

mà AD là đường phân giác của \(\widehat{BAC}\) hay \(\widehat{BAE}\) thuộc tam giác ABE

=> Tam giác ABE cân tại A

Bài 9.40

Một sợi dây thép dài 1,2m. Cần đánh dấu trên sợi dây thép đó hai điểm để khi uốn gập nó lại tại hai điểm đó sẽ tạo thành một tam giác cân có một cạnh dài 30cm (H9.54). Em hãy mô tả các cách đánh dấu hai điểm trên sợi dây thép.