Toán 11 Bài 27: Thể tích Giải Toán 11 Kết nối tri thức trang 61, 62, 63 - Tập 2

Bài trước

Mục lục

Bài sau

Giải Toán 11 Bài 27: Thể tích là tài liệu vô cùng hữu ích giúp các em học sinh lớp 11 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 11 Kết nối tri thức với cuộc sống tập 2 trang 61, 62, 63.

Toán 11 Kết nối tri thức trang 63 tập 2 được biên soạn đầy đủ, chi tiết trả lời các câu hỏi từ bài 7.28 đến 7.32 giúp các bạn có thêm nhiều nguồn ôn tập đối chiếu với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết giải Toán 11 trang 63 Kết nối tri thức với cuộc sống tập 2 mời các bạn cùng theo dõi tại đây.

Toán 11 Bài 27: Thể tích

Giải Toán 11 trang 63 Kết nối tri thức - Tập 2

Giải Toán 11 trang 63 Kết nối tri thức - Tập 2

Bài 7.28

Cho khối chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b. Tính thể tích của khối chóp đó. Từ đó suy ra thể tích của khối tứ diện đều có cạnh bằng a.

Gợi ý đáp án

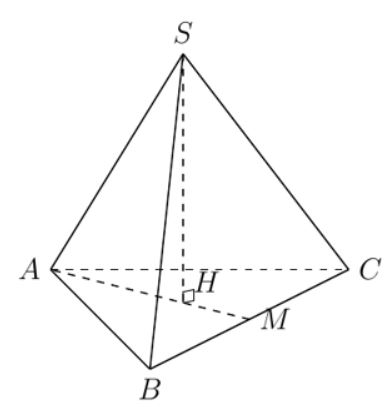
Gọi H là tâm của tam giác đều ABC. Gọi M là trung điểm của BC.

Vì tam giác ABC đều cạnh a nên:

$AM=\frac{a\sqrt{3}}{2} và AH=\frac{2}{3}AM=\frac{a{\sqrt{3}}}{3}$ $AM=\frac{a\sqrt{3}}{2} và AH=\frac{2}{3}AM=\frac{a{\sqrt{3}}}{3}$

Tam giác SAH vuông tại H

$\Rightarrow SH=\sqrt{SA^{2}-AH^{2}}=\sqrt{a^{2}-\frac{a^{2}}{3}}=\frac{a\sqrt{6}}{3}$ $\Rightarrow SH=\sqrt{SA^{2}-AH^{2}}=\sqrt{a^{2}-\frac{a^{2}}{3}}=\frac{a\sqrt{6}}{3}$

Thể tích khối chóp S.ABC là:

$V=\frac{1}{3}.S_{ABC}.SH=\frac{1}{3}.\frac{a^{2}\sqrt{3}}{4}.\frac{a\sqrt{6}}{3}=\frac{a^{3}\sqrt{2}}{12}$ $V=\frac{1}{3}.S_{ABC}.SH=\frac{1}{3}.\frac{a^{2}\sqrt{3}}{4}.\frac{a\sqrt{6}}{3}=\frac{a^{3}\sqrt{2}}{12}$

Do đó, thể tích của khối tứ diện đều có cạnh bằng a là:

$V=\frac{1}{3}.S_{0}.h=\frac{1}{3}a^{2}.\frac{\sqrt{2}}{2}a=\frac{a^{3}\sqrt{2}}{6}$ $V=\frac{1}{3}.S_{0}.h=\frac{1}{3}a^{2}.\frac{\sqrt{2}}{2}a=\frac{a^{3}\sqrt{2}}{6}$

Bài 7.29

Cho khối lăng trụ đứng ABC.A'B'C' có AA'= 5 cm, AB = 6 cm, BC = 2 cm, $\widehat{ABC} = 150 \circ$ $\widehat{ABC} = 150 \circ$. Tính thể tích của khối lăng trụ.

Gợi ý đáp án

Gọi O là trung điểm của SA ta có $OB=(\frac{b}{2})^{2} và SB=\sqrt{a^{2}+(\frac{b}{2})^{2}}$ $OB=(\frac{b}{2})^{2} và SB=\sqrt{a^{2}+(\frac{b}{2})^{2}}$.

Áp dụng định lý Pytago cho tam giác vuông SBO, ta có:

$h=SO=\sqrt{SB^{2}-BO^{2}}=\sqrt{a^{2}+(\frac{b}{2})^{2}} -\frac{a}{2}$ $h=SO=\sqrt{SB^{2}-BO^{2}}=\sqrt{a^{2}+(\frac{b}{2})^{2}} -\frac{a}{2}$

Công thức tính thể tích khối chóp đều, ta có:

$V=\frac{1}{3}S_{đáy} h \frac{1}{3}a^{2}(\sqrt{a^{2}+(\frac{b}{2})^{2}}-\frac{a}{2})$ $V=\frac{1}{3}S_{đáy} h \frac{1}{3}a^{2}(\sqrt{a^{2}+(\frac{b}{2})^{2}}-\frac{a}{2})$

$V_{Tứ diện}=\frac{\sqrt{2}}{12}a^{3}$ $V_{Tứ diện}=\frac{\sqrt{2}}{12}a^{3}$

Bài 7.30

Cho khối chóp đều S.ABCD, đáy có cạnh 6 cm. Tính thể tích của khối chóp đó trong các trường hợp sau.

a) Cạnh bên tạo với mặt đáy một góc bằng 60^∘

b) Mặt bên tạo với mặt đáy một góc bằng 45^∘.

Gợi ý đáp án

a) Thể tích của khối chóp theo công thức:

$V=\frac{1}{3}S_{day}.h=\frac{1}{3}.\frac{\sqrt{3}}{4}.^{2}.6=36\sqrt{3}cm^{3}$ $V=\frac{1}{3}S_{day}.h=\frac{1}{3}.\frac{\sqrt{3}}{4}.^{2}.6=36\sqrt{3}cm^{3}$

b) Công thức tính thể tích của khối chóp, ta có:

$V=\frac{1}{3}S_{day}.h=\frac{1}{3}.\frac{1}{4}.6^{2}.h=3h cm^{3}$ $V=\frac{1}{3}S_{day}.h=\frac{1}{3}.\frac{1}{4}.6^{2}.h=3h cm^{3}$

Mà Trong đó $\widehat{BDC} = 45^{\circ}$ $\widehat{BDC} = 45^{\circ}$ và b = c , do đó $b=6\sqrt{\frac{2}{3}}$ $b=6\sqrt{\frac{2}{3}}$

Ta sẽ tính chiều cao h bằng cách sử dụng định lí Pytago trong tam giác BDC:

$h^{2}=BD^{2}-(\frac{b}{2})^{2}=(\frac{6\sqrt{2}}{2\sqrt{3}})^{2}=6$ $h^{2}=BD^{2}-(\frac{b}{2})^{2}=(\frac{6\sqrt{2}}{2\sqrt{3}})^{2}=6$

Vậy thể tích của khối chóp là 3h = $3\sqrt{6} \mathrm{cm^3}$ $3\sqrt{6} \mathrm{cm^3}$

Bài 7.31

Cho khối lăng trụ ABC.A'B'C' có đáy là các tam giác đều cạnh a, A'A = A'B = A'C = b. Tính thể tích của khối lăng trụ.

Bài 7.32

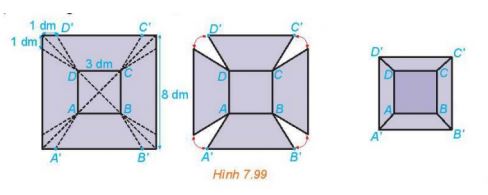
Từ một tấm tôn hình vuông có cạnh 8 dm, bác Hùng cắt bỏ bốn phần như nhau ở bốn góc, sau đó bác hàn các mép lại để được một chiếc thùng (không có nắp ) như Hình 7.99.

a) Giải thích vì sao chiếc thùng có dạng hình chóp cụt.

b) Tính cạnh bên của thùng.

c) Hỏi thùng có thể chứa được nhiều nhất bao nhiêu lít nước?