Toán 11 Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng Giải Toán 11 Kết nối tri thức trang 38, 39, 40, 41,42, 43 - Tập 2

Giải Toán 11 Bài 24: Phép chiếu vuông góc - Góc giữa đường thẳng và mặt phẳng là tài liệu vô cùng hữu ích giúp các em học sinh lớp 11 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 11 Kết nối tri thức với cuộc sống tập 2 trang 38, 39, 40, 41,42, 43.

Toán 11 Kết nối tri thức trang 42, 43 tập 2 được biên soạn đầy đủ, chi tiết trả lời các câu hỏi từ bài 7.10 đến 7.15 giúp các bạn có thêm nhiều nguồn ôn tập đối chiếu với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết giải Toán 11 trang 42, 43 Kết nối tri thức với cuộc sống tập 2 mời các bạn cùng theo dõi tại đây.

Giải Toán 11 trang 42, 43 Kết nối tri thức - Tập 2

Bài 7.10

Cho hình chóp S.ABC có SA ⊥ (ABC), tam giác ABC vuông tại B.

a) Xác định hình chiếu của điểm S trên mặt phẳng (ABC).

b) Xác định hình chiếu của tam giác SBC trên mặt phẳng (ABC).

c) Xác định hình chiếu của tam giác SBC trên mặt phẳng (SAB).

Gợi ý đáp án

a) Ta vẽ đường thẳng vuông góc từ S xuống (ABC), gọi M là giao điểm của đường thẳng đó với mặt phẳng (ABC). Khi đó, hình chiếu của điểm S trên mặt phẳng (ABC) chính là điểm M.

b) Lần lượt vẽ đường thẳng vuông góc từ S đến SB, SC và BC, gọi I, J và K lần lượt là các giao điểm của các đường thẳng đó với mặt phẳng (ABC). Khi đó, tam giác SBC được chiếu lên mặt phẳng (ABC) thành tam giác IJK.

c) Ta vẽ đường thẳng vuông góc từ B đến SC, gọi L là giao điểm của đường thẳng đó với đoạn thẳng SC. Tiếp theo, ta vẽ đường thẳng qua L và vuông góc với SA, gọi N là giao điểm của đường thẳng đó với đoạn thẳng SA. Khi đó, tam giác SBC được chiếu lên mặt phẳng (SAB) thành tam giác S'BN, trong đó S' là hình chiếu của điểm S lên mặt phẳng (SAB).

Bài 7.11

Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA ⊥ (ABCD) và SA = \(a\sqrt{2}\).

a) Tính góc giữa SC và mặt phẳng (ABCD).

b) Tính góc giữa BD và mặt phẳng (SAC).

c) Tìm hình chiếu của SB trên mặt phẳng (SAC).

Gợi ý đáp án

a) Ta có \(\vec{SC} = \vec{SA}+\vec{AC}\). Vì ABCD là hình vuông cạnh a, nên AC = BD = a\sqrt{2} . Áp dụng định lí cosin trong tam giác SAC , ta có:

\(cos ( SC,(ABCD))= \frac{\vec{SC}.\vec{SA}}{SC.SA}=\frac{a\sqrt{2}}{2a\sqrt{2}}=\frac{1}{2}\)

Do đó, góc giữa SC và mặt phẳng (ABCD) bằng \(\arccos\frac{1}{2} = 60^\circ .\)

Bài 7.12

Cho hình đóp S.ABC có SA. (ABC), Tam giác ABC vuông tại B, SA = AB = BC = a

a) Xác định hình chiếu của A trên mặt phẳng (SBC)

b) Tính góc giữa SC và mặt phẳng (ABC).

Gợi ý đáp án

a) Vì SA vuông góc với mặt phẳng (ABC) và SA = AB = a, nên ta có thể kẻ đường thẳng vuông góc với mặt phẳng (ABC) và đi qua A. Gọi đường thẳng này là d1

Từ B, kẻ đường thẳng vuông góc với SB và đi qua A. Gọi đường thẳng này là d2

Giao d1 và d2 tại điểm M

Kết nối A với M. Đoạn thẳng này chính là hình chiếu của A trên mặt phẳng (SBC).

Vậy hình chiếu của A trên mặt phẳng (SBC) là đoạn thẳng AM

b) Góc giữa SC và mặt phẳng (ABC) chính là góc giữa SC và đường thẳng AB, được tính bằng công thức:

\(cos(SC, AB) = \frac{SC \cdot AB}{\left| SC \right| \cdot \left| AB \right|}\)

Do SA = AB = BC = a, ta có SC = 2a. Từ đó:

\(cos(SC, AB) = \frac{2a \cdot a}{\left| 2a \right| \cdot \left| a \right|} = \frac{2}{\sqrt{5}}\)

Suy ra, góc giữa SC và mặt phẳng (ABC) là:

\(sin^{-1}\left(\frac{2}{\sqrt{5}}\right) \approx 63.43^{\circ}\)

Bài 7.13

Gợi ý đáp án

a) Gọi A là giao điểm của đường thẳng SM và (P), B là giao điểm của đường thẳng SM' và (P). Khi đó, ta có:

AH vuông góc với (P), BM' vuông góc với (P).

AH = SM, BM' = SM'.

AB là hình chiếu của đoạn thẳng SM' lên (P), A'B là hình chiếu của đoạn thẳng SM lên (P).

Do đó, ta có hai tam giác AHM và A'HM' cân tại H và H', tương ứng. Từ đó, ta suy ra được hai hình chiếu HM và HM' tương ứng của đường xiên SM và SM' bằng nhau.

b) Gọi A là giao điểm của đường thẳng SM và (P), B là giao điểm của đường thẳng SM' và (P). Khi đó, ta có:

AB là hình chiếu của đoạn thẳng SM' lên (P), AM là hình chiếu của đoạn thẳng SM lên (P).

Góc giữa AB và (P) lớn hơn góc giữa AM và (P), do đường xiên SM lớn hơn đường xiên SM'.

Từ đó, ta suy ra được HM' > HM'' suy ra SM > SM'

Bài 7.14

Gợi ý đáp án 

Hai máy bay có cùng độ lớn vận tốc nên sau 1 phút kể từ khi cất cánh hai máy bay bay được quãng đường bằng nhau tức AM = A'M'.

Xét tam giác ABM vuông tại B có BM = AM × sin10°

Xét tam giác A'CM' vuông tại C có CM' = A'M' × sin15°.

Mà sin10° < sin15° nên BM < CM'.

Vậy sau 1 phút cất cánh, máy bay có góc cất cánh 15° ở độ cao lớn hơn so với máy bay có góc cất cánh 10°.

Bài 7.15

Gợi ý đáp án

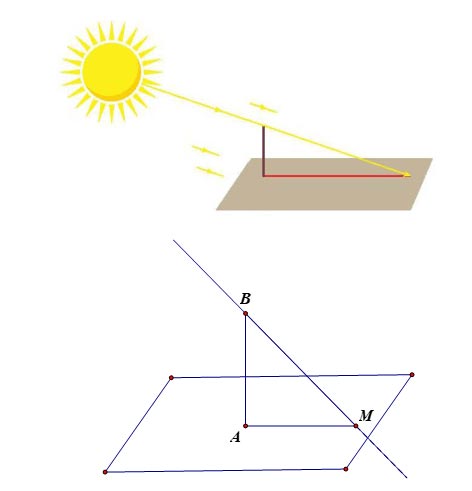
Để đo góc giữa đường thẳng chứa tia sáng mặt trời và mặt phẳng nằm ngang tại một vị trí và một thời điểm ta đưa về bài toán trên sân phẳng có một cây cột AB vuông góc với mặt sân, dưới ánh sáng mặt trời, bóng của cây cột trên sân AM chính là hình chiếu của cây cột. Khi đó góc giữa đường thẳng chứa tia sáng mặt trời và mặt phẳng nằm ngang chính là góc BAM

Xét tam giác BAM vuông tại A, có: tan góc BAM= AB/AM

Từ đó ta tính được góc BMA.