Toán 11 Bài 4: Hai mặt phẳng song song Giải Toán 11 Chân trời sáng tạo trang 113, 114, 115, 116, 117, 118, 119, 120

Toán lớp 11 tập 1 trang 113, 114, 115, 116, 117, 118, 119, 120 Chân trời sáng tạo là tài liệu vô cùng hữu ích mà Eballsviet.com muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 tham khảo.

Giải Toán 11 Chân trời sáng tạo bài 4 Hai mặt phẳng song song được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 119, 120. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán 11 tập 1 bài 4 Hai mặt phẳng song song Chân trời sáng tạo, mời các bạn cùng theo dõi tại đây.

Toán 11 Bài 4: Hai mặt phẳng song song

Bài 1

Trong mặt phẳng (P) cho hình bình hành ABCD. Ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với (P) lần lượt đi qua các điểm A,B,C,D. Một mặt phẳng (Q) cắt bốn nửa đường thẳng nói trên tại A', B', C', D'. Chứng minh rằng:

AA' + CC' = BB' + DD'

Bài làm

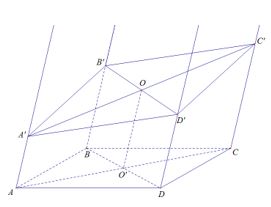
AB//CD nên AB // (CDD'C'), AA' // DD' nên DD' // (CDD'C')

Ta có (ABB'A') đi chứa 2 đường thẳng cắt nhau AB và AA' cùng song song với (CDD'C') nên (ABB'A') // (CDD'C')

AD // BC nên AD // (BCC'B'), AA' // BB' nên AA' // (BCC'B')

Ta có (ADD'A') đi chứa 2 đường thẳng cắt nhau AD và AA' cùng song song với (CBB'C') nên (ADD'A') // (CBB'C')

Mặt phẳng (A'B'C'D') cắt hai mặt phẳng song song (ABB'A') và (CDD'C') lần lượt tại A'B' và CD' nên AB' // CD'

Mặt phẳng (A'B'C'D') cắt hai mặt phẳng song song (ADD'A') và (CBB'C') lần lượt tại A'D' và CB' nên AD' // CB'

Suy ra A'B'C'D' là hình bình hành, nên A'C' cắt B'D' tại trung điểm O

Gọi O' là giao của AC và BD

Mặt phẳng (AA'C'C) cắt hai mặt phẳng song song (ABB'A') và (CDD'C') lần lượt tại AA' và CC' nên AA' // CC'

Trong hình thang ACC'A' có OO' là đường trung bình nên AA' + CC' = 2OO'

Mặt phẳng (BDD'B') cắt hai mặt phẳng song song (ABB'A') và (CDD'C') lần lượt tại BB' và DD' nên BB'//DD'

Trong hình thang BDD'B' có OO' là đường trung bình nên BB' + DD' = 2OO'

Vậy AA' + CC' = BB' + DD'

Bài 2

Cho hình chóp S.ABCD, đáy ABCD là hình bình hành tâm O có O là giao điểm của hai đường chéo. Gọi M, N lần lượt là trung điểm của SA, SD

a) Chứng minh rằng (OMN) // (SBC)

b) Gọi E là trung điểm của AB và F là một điểm thuộc ON. Chứng minh EF song song với (SBC).

Bài làm

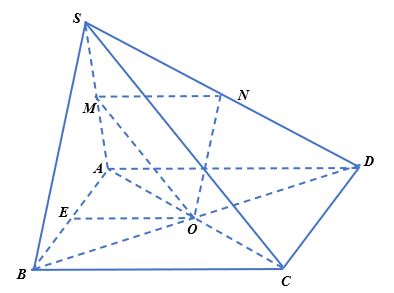
a) Trong tam giác SBD có ON là đường trung bình nên ON // SB. Suy ra MN // (SBC)

Trong tam giác SAD có MN là đường trung bình nên MN // AD. Mà AD // BC nên MN // BC. Suy ra MN // (SBC)

Mặt phẳng (OMN) chứa hai đường thẳng cắt nhau MN và ON cùng song song với (SBC)

Do đó, (OMN) // (SBC)

b) Trong tam giác ABC có OE là đường trung bình nên OE // BC. Suy ra OE // (SBC)

Mà (OMN) // (SBC) nên E ∈ (OMN)

Ta có: (OMN) // (SBC); EF ⊂ (OMN) nên EF // (SBC)

Bài 3

Cho hai hình vuông ABCD và ABEF ở hai mặt phẳng khác nhau. Trên các đường chéo AC và BF lần lượt lấy các điểm M, N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M, N lần lượt cắt AD, AF tại M', N'.

a) Chứng minh (CBE) // (ADF)

b) Chứng minh (DEF) // (MNN'M')

Bài làm

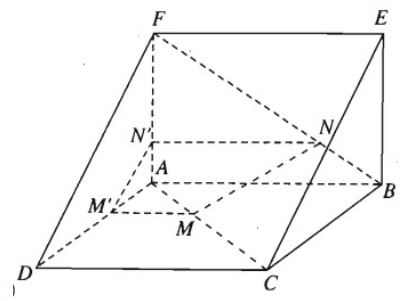
a) Ta có AD // BC nên AD // (BEC)

AF // BE nên AF // (BEC)

Mặt phẳng (ADF) đi qua hai đường thẳng cắt nhau AD và AF cùng song song với (CBE) nên (ADF) // (CBE)

b) Vì ABCD và ABEF là hình vuông có cạnh bằng nhau nên AC = BF

Trong tam giác ADC có MM' // CD nên \(\frac{AM′}{AD}\) = \(\frac{AM}{AC}\)

Trong tam giác ABF có NN' // AB nên \(\frac{AN′}{AF}\) = \(\frac{BN}{BF}\)

Mà AM = BN nên \(\frac{AN′}{AF}\) = \(\frac{AM′}{AD}\). Suy ra M'N' // DF. Nên M'N' // (DEF)

Ta có MM' // AB // EF nên MM' // (DEF)

Mặt phẳng (MNN'M') chứa hai đường thẳng cắt nhau MM' và M'N' cùng song song với (DEF)

Do đó, (MNN'M') // (DEF)

Bài 4

Cho hình hộp ABCD.A'B'C'D'. Gọi G₁ và G₂ lần lượt là trọng tâm của hai tam giác BDA' và B'D'C. Chứng minh G₁ và G₂ chia đoạn AC' thành ba phần bằng nhau.

Bài làm

Gọi O là giao điểm của AC và BD, O' là giao điểm của A'C' và B'D', I là giao điểm của AC' và A'C

Do ACCA' là hình bình hành nên I là trung điểm của A'C

G₁ là trọng tâm tam giác BDA' nên \(\frac{A^{'} G_{1} }{AO}\) = \(\frac{2}{3}\)

Tam giác AA'C có A'O là trung tuyến, \(\frac{A^{'} G_{1} }{AO}\) = \(\frac{2}{3}\) nên G₁ là trọng tâm của tam giác AA'C.

Mà I là trung điểm A'C nên G₁ ∈ AI và AG₁ = \(\frac{2}{3}\)AI

Mà AI = \(\frac{1}{2}\)AC′ nên AG₁ = \(\frac{1}{3}\)AC′

Tương tự ta có C′G₂ = \(\frac{1}{3}\)AC′

Suy ra G₁, G₂ chia AC' thành 3 đoạn thẳng bằng nhau

Bài 5

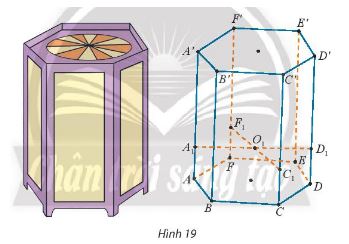
Để làm một khung lồng đèn kéo quân hình lăng trụ lục giác ABCDEF.A'B'C'D'E'F', Bình gắn hai thanh tre A₁D₁,F₁C₁ song song với mặt phẳng đáy và cắt nhau tại O₁ (Hình 19)

a) Xác định giao tuyến của mp(A₁D₁,F₁C₁) với các mặt bên của lăng trụ

b) Cho biết A′A₁= 6AA₁ và AA' = 70 cm. Tính CC₁ và C₁C′

Bài làm

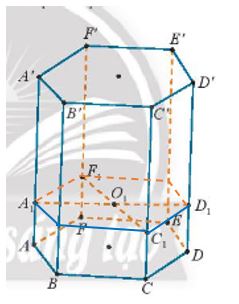
a) Do mặt phẳng (A₁C₁D₁F₁) chứa hai đường thẳng cắt nhau A₁D₁ và C₁F₁ và cùng song song với mặt phẳng (ABCDEF)

Nên (A₁C₁D₁F₁) // (ABCDEF)

Gọi B₁,E₁ lần lượt là giao của mặt phẳng (A₁C₁D₁F₁) với BB' và EE'

Ta có giao tuyến của (A₁C₁D₁F₁) với các mặt bên của lăng trụ là A₁B₁, B₁C₁, C₁D₁, D₁E₁, E₁F₁, F₁A₁

b) Ta có: A′A₁ = 6AA₁; AA′ = 70 nên AA₁ = 10

Do (ACC'A') cắt hai mặt phẳng (A₁C₁D₁F₁) // (ABCDEF) lần lượt tại A1C1 và AC nên A₁C₁ // AC

Mà AA₁ // CC₁nên tứ giác AA₁C₁C là hình bình hành.

Suy ra CC₁ = AA₁ = 10

Mà CC' = AA' = 70

Nên C₁C′ = 70 − 10 = 60

Bài 6

Chỉ ra các mặt phẳng song song trong mỗi hình sau. Tìm thêm một số ví dụ khác về các mặt phẳng song song trong thực tế.

Bài làm

Trong hình a: các mặt tấm pin điện năng lượng mặt trời song song với nhau

Trong hình b: Các mặt của toà nhà song song với nhau

Một số ví dụ khác về mặt phẳng song song: mặt của các bậc cầu thang, mặt phẳng của các bức tường đối diện nhau

II. Luyện tập Hai mặt phẳng song song