Toán 11 Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện Giải Toán 11 Chân trời sáng tạo trang 82, 83, 84, 85

Bài trước

Mục lục

Bài sau

Toán lớp 11 tập 2 trang 82, 83, 84, 85 Chân trời sáng tạo là tài liệu vô cùng hữu ích mà Eballsviet.com muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 tham khảo.

Giải Toán 11 Chân trời sáng tạo bài 5 Góc giữa đường thẳng và mặt phẳng - Góc nhị diện được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 85. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán 11 tập 2 bài 5 Khoảng cách trong không gian Chân trời sáng tạo, mời các bạn cùng theo dõi tại đây.

Giải Toán 11 Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Toán lớp 11 tập 2 trang 85 - Chân trời sáng tạo

Toán lớp 11 tập 2 trang 85 - Chân trời sáng tạo

Bài 1

Cho tứ diện đều ABCD, Vẽ hình bình hành BCED

a) Tìm góc giữa đường thẳng AB và (BCD)

b) Tìm góc phẳng nhị diện [A,CD,B]; [A,CD,E]

Bài làm

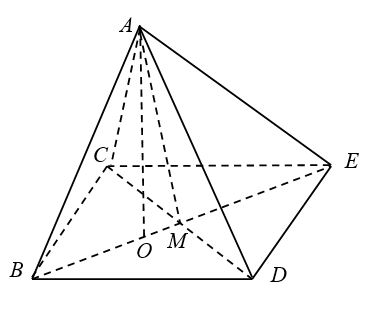
a) Gọi O là tâm tam giác BCD. Do tứ diện ABCD đều nên AO $\perp$ $\perp$ (BCD)

Nên góc giữa đường thẳng AB và (BCD) là $\widehat{ABO}$ $\widehat{ABO}$

Gọi a là độ dài cạnh của tứ diện đều ABCD.

O là trọng tâm tam giác BCD nên BO = $\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$ $\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$

$cos\widehat{ABO} = \frac{BO}{AB} =\frac{\sqrt{3}}{3} nên \widehat{ABO} = 54,7^{o}$ $cos\widehat{ABO} = \frac{BO}{AB} =\frac{\sqrt{3}}{3} nên \widehat{ABO} = 54,7^{o}$

Suy ra góc giữa đường thẳng AB và (BCD} bằng 54,7^o

b) Gọi M là trung điểm CD.

BCED là hình bình hành nên ED = BC = a, CE = BD = a. Nên BCED là hình thoi

Ta có BM $\perp$ $\perp$ CD, EM $\perp$ $\perp$ CD

Mà CD $\perp$ $\perp$ AO nên CD $\perp$ $\perp$ (ABM) . Suy ra CD $\perp$ $\perp$ AM

[A, CD, B] = $\widehat{AMB}$ $\widehat{AMB}$, [A, CD, E] = $\widehat{AME}$ $\widehat{AME}$

Ta có: OM = $\frac{1}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6}$ $\frac{1}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6}$

AO = $\sqrt{a^{2}-(\frac{a\sqrt{3}}{3})^{2}} = \frac{a\sqrt{6}}{3}$ $\sqrt{a^{2}-(\frac{a\sqrt{3}}{3})^{2}} = \frac{a\sqrt{6}}{3}$

$tan\widehat{AMO} = \frac{AO}{OM} = 2\sqrt{2} .$ $tan\widehat{AMO} = \frac{AO}{OM} = 2\sqrt{2} .$

Nên $\widehat{AMO}= 70,5^{o}, \widehat{AME} = 180^{o} - 70,5^{o} = 109,5^{o}$ $\widehat{AMO}= 70,5^{o}, \widehat{AME} = 180^{o} - 70,5^{o} = 109,5^{o}$

Vậy [A, CD, B] = 70,5^o , [A, CD, E] = 109,5^o

Bài 2

Cho hình chóp tứ giác đều S.ABCD có O là tâm của đáy và có tất cá các cạnh bằng nhau.

a) Tìm góc giữa đường thẳng SA và (ABCD)

b) Tìm góc phẳng nhị diện [A, SO, B], [S, AB, O]

Bài làm

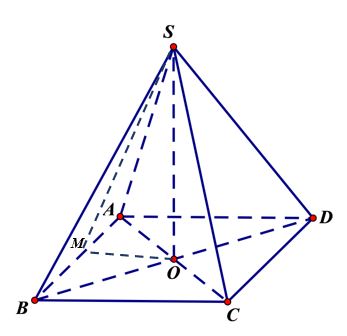
a) Gọi a là độ dài các cạnh của S.ABCD

Gọi O là tâm của hình vuông ABCD. Ta có: SO ⊥ (ABCD)

Do đó, góc giữa SA và (ABCD) là $\widehat{OSA}$ $\widehat{OSA}$

Ta có: AO = $\frac{a\sqrt{2}}{2}$ $\frac{a\sqrt{2}}{2}$

$cos\widehat{SOA} = \frac{AO}{SA} = \frac{\sqrt{2}}{2}$ $cos\widehat{SOA} = \frac{AO}{SA} = \frac{\sqrt{2}}{2}$. Nên $\widehat{SOA} = 45^{o}$ $\widehat{SOA} = 45^{o}$

Vậy góc giữa SA và (ABCD) là 45^o

b)Vì SO $\perp$ $\perp$ (ABCD) nên SO $\perp$ $\perp$ AO, SO $\perp$ $\perp$ BO

[A, SO, B] = $\widehat{AOB} = 90^{o}$ $\widehat{AOB} = 90^{o}$

Kẻ M là trung điểm của AB. Ta có: SM $\perp$ $\perp$ AB, OM $\perp$ $\perp$ AB

[S, AB, O] = $\widehat{SMO}$ $\widehat{SMO}$

Tam giác SAB đều có SM là trung tuyến nên SM = $\frac{a\sqrt{3}}{2}$ $\frac{a\sqrt{3}}{2}$

$cos\widehat{SMO} = \frac{MO}{SM} = \frac{1}{\sqrt{3}} nên \widehat{SMO} = 54,7^{o}$ $cos\widehat{SMO} = \frac{MO}{SM} = \frac{1}{\sqrt{3}} nên \widehat{SMO} = 54,7^{o}$

Vậy [S, AB, O] = 54,7^o

Bài 3

Cho hình chóp cụt lục giác đều ABCDEF.A'B'C'D'E'F' với O và O' là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là a và $\frac{a}{2}$ $\frac{a}{2}$, OO' = a

a) Tìm góc giữa cạnh bên và mặt đáy

b) Tìm góc phẳng nhị diện [O, AB, A'], [O', A'B; A]

Bài làm

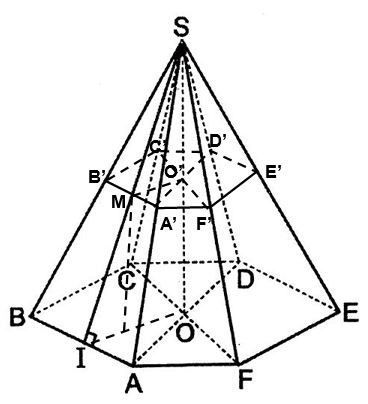
a) OO' = a nên SO = 2a

SO $\perp$ $\perp$ (ABCDEF) nên góc giữa cạnh bên và đáy là $\widehat{SAO}$ $\widehat{SAO}$

Ta có: AO = BC = a; SO = 2OO' = 2a

$tan\widehat{SAO} =\frac{SO}{OA} =2$ $tan\widehat{SAO} =\frac{SO}{OA} =2$

Nên $\widehat{SAO} = 63,4^{o}$ $\widehat{SAO} = 63,4^{o}$

b) Kẻ MH $\perp$ $\perp$ (ABCDEF) nên MH = OO' = a

MO' = HO = $\frac{a\sqrt{3}}{6} ; OI =\frac{a\sqrt{3}}{2}$ $\frac{a\sqrt{3}}{6} ; OI =\frac{a\sqrt{3}}{2}$

IH = OI - OH = $\frac{a\sqrt{3}}{6}$ $\frac{a\sqrt{3}}{6}$

$tan\widehat{MIO} = \frac{MH}{IH} = \frac{6}{\sqrt{3}} nên \widehat{MIO} = 73,9^{o}$ $tan\widehat{MIO} = \frac{MH}{IH} = \frac{6}{\sqrt{3}} nên \widehat{MIO} = 73,9^{o}$

[O, AB, A'] = $\widehat{MIO} = 73,9^{o}$ $\widehat{MIO} = 73,9^{o}$

[O',A'B', A] = $\widehat{IMO} = 180^{o} - 73,9^{o}=106,1^{o}$ $\widehat{IMO} = 180^{o} - 73,9^{o}=106,1^{o}$

Bài 4

Một con dốc có dạng hình lăng trụ đứng tam giác với kích thước như trong Hình 9

a) Tính số đo góc giữa đường thẳng CA' và (CC'B'B)

b) Tính số đo góc nhị diện cạnh CC'

Bài 5

Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 14 m và 10 m. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng 135^o. Tính số mét khối cần di chuyển ra khỏi hầm