Toán 11 Bài 4: Hàm số lượng giác và đồ thị Giải Toán 11 Chân trời sáng tạo trang 25, 26, 27 ... 33

Bài trước

Mục lục

Bài sau

Toán 11 Chân trời sáng tạo tập 1 trang 25→33 là tài liệu vô cùng hữu ích mà Eballsviet.com muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 tham khảo.

Giải Toán 11 Chân trời sáng tạo Bài 4 Hàm số lượng giác và đồ thị được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 32, 33. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết giải Toán 11 Chân trời sáng tạo tập 1 trang 32, 33 mời các bạn cùng theo dõi tại đây.

Giải Toán 11 Bài 4: Hàm số lượng giác và đồ thị

I. Toán 11 Chân trời sáng tạo tập 1 trang 32, 33

Bài 1

Các hàm số dưới đây có là hàm số chẵn hay hàm số lẻ không?$a)$ $y = 5 \sin^2x + 1$ $y = 5 \sin^2x + 1$;$b)$ $y = \cos{x} + \sin{x}$ $y = \cos{x} + \sin{x}$;$c)$ $y = \tan2x$ $y = \tan2x$.

Trả lời:

$a)$ $y = 5\sin^2x + 1$ $y = 5\sin^2x + 1$

Hàm số $y = 5\sin^2x + 1$ $y = 5\sin^2x + 1$ có tập xác định là $\mathbb{R}$ $\mathbb{R}$.

Với mọi $x \in \mathbb{R}$ $x \in \mathbb{R}$ ta có $\ – \ x \in \mathbb{R}$ $\ – \ x \in \mathbb{R}$

Ta có: $y(\ – \ x) = 5\sin^2{(\ – \ x)} + 1 = 5\sin^2x + 1 = y(x)$ $y(\ – \ x) = 5\sin^2{(\ – \ x)} + 1 = 5\sin^2x + 1 = y(x)$

Do đó hàm số $y = 5\sin^2x + 1$ $y = 5\sin^2x + 1$ là hàm số chẵn.

$b)$ $y = \cos{x} + \sin{x}$ $y = \cos{x} + \sin{x}$

Hàm số $y = \cos{x} + \sin{x}$ $y = \cos{x} + \sin{x}$ có tập xác định là $\mathbb{R}$ $\mathbb{R}$.

Với mọi $x \in \mathbb{R}$ $x \in \mathbb{R}$ ta có $\ – \ x \in \mathbb{R}$ $\ – \ x \in \mathbb{R}$

Ta có: $y(\ – \ x) = \cos{(\ – \ x)} + \sin{(\ – \ x)} = \cos{x} \ – \ \sin{x}$ $y(\ – \ x) = \cos{(\ – \ x)} + \sin{(\ – \ x)} = \cos{x} \ – \ \sin{x}$

Vậy hàm số $y = \cos{x} + \sin{x}$ $y = \cos{x} + \sin{x}$ không là hàm số chẵn, không là hàm số lẻ. (do $y(\ – \ x) \neq y(x) \text{ và } y(\ – \ x) \neq \ – \ y(x)$ $y(\ – \ x) \neq y(x) \text{ và } y(\ – \ x) \neq \ – \ y(x)$)

$c)$ $y = \tan2x$ $y = \tan2x$

Hàm số xác định trên tập $D = \mathbb{R} \setminus \{k\displaystyle \frac{\pi}{4}; k \in \mathbb{Z}\}$ $D = \mathbb{R} \setminus \{k\displaystyle \frac{\pi}{4}; k \in \mathbb{Z}\}$

Với mọi $x \in \mathbb{D}$ $x \in \mathbb{D}$ ta có $\ – \ x \in \mathbb{D}$ $\ – \ x \in \mathbb{D}$

Ta có: $y(\ – \ x) = \tan{2 (\ – \ x)} = \ – \ \tan2x = \ – \ y(x)$ $y(\ – \ x) = \tan{2 (\ – \ x)} = \ – \ \tan2x = \ – \ y(x)$

Vậy hàm số $y = \tan2x$ $y = \tan2x$ là hàm số lẻ.

Bài 2

Tìm tập xác định của các hàm số sau:$a)$ $y = \displaystyle \frac{1}{\cos{x}}$ $y = \displaystyle \frac{1}{\cos{x}}$;$b)$ $y = \tan{\left(x + \displaystyle \frac{\pi}{4}\right)}$ $y = \tan{\left(x + \displaystyle \frac{\pi}{4}\right)}$;$c)$ $y = \displaystyle \frac{1}{2 \ – \ \sin^2x}$ $y = \displaystyle \frac{1}{2 \ – \ \sin^2x}$.

Trả lời:

$a)$ $y = \displaystyle \frac{1}{\cos{x}}$ $y = \displaystyle \frac{1}{\cos{x}}$

Hàm số xác định khi và chỉ khi $\cos{x} \neq 0$ $\cos{x} \neq 0$

$\Leftrightarrow x \neq \displaystyle \frac{\pi}{2} + k\pi, k \in \mathbb{Z}$ $\Leftrightarrow x \neq \displaystyle \frac{\pi}{2} + k\pi, k \in \mathbb{Z}$

Vậy tập xác định của hàm số là $D = \mathbb{R} \setminus \{\displaystyle \frac{\pi}{2} + k\pi, k \in \mathbb{Z}\}$ $D = \mathbb{R} \setminus \{\displaystyle \frac{\pi}{2} + k\pi, k \in \mathbb{Z}\}$

$b)$ $y = \tan{\left(x + \displaystyle \frac{\pi}{4}\right)}$ $y = \tan{\left(x + \displaystyle \frac{\pi}{4}\right)}$

Hàm số xác định khi và chỉ khi $\cos{\left(x + \displaystyle \frac{\pi}{4}\right)} \neq 0$ $\cos{\left(x + \displaystyle \frac{\pi}{4}\right)} \neq 0$

$\Leftrightarrow x + \displaystyle \frac{\pi}{4} \neq \displaystyle \frac{\pi}{2} + k\pi$ $\Leftrightarrow x + \displaystyle \frac{\pi}{4} \neq \displaystyle \frac{\pi}{2} + k\pi$

$\Leftrightarrow x \neq \displaystyle \frac{\pi}{4} + k\pi, k \in \mathbb{Z}$ $\Leftrightarrow x \neq \displaystyle \frac{\pi}{4} + k\pi, k \in \mathbb{Z}$

Vậy tập xác định của hàm số là $D = \mathbb{R} \setminus \{\displaystyle \frac{\pi}{4} + k\pi, k \in \mathbb{Z}\}$ $D = \mathbb{R} \setminus \{\displaystyle \frac{\pi}{4} + k\pi, k \in \mathbb{Z}\}$

$c)$ $y = \displaystyle \frac{1}{2 \ – \ \sin^2x}$ $y = \displaystyle \frac{1}{2 \ – \ \sin^2x}$

Hàm số xác định khi và chỉ khi $2 \ – \ \sin^2x \neq 0$ $2 \ – \ \sin^2x \neq 0$

$\Leftrightarrow \sin^2x \neq 2$ $\Leftrightarrow \sin^2x \neq 2$ luôn đúng vì $\ – \ 1 \leq \sin{x} \leq 1 \text{ nên } \sin^2x \leq 1 \neq 2$ $\ – \ 1 \leq \sin{x} \leq 1 \text{ nên } \sin^2x \leq 1 \neq 2$

Vậy tập xác định của hàm số là $\mathbb{R}$ $\mathbb{R}$

Bài 3

Tìm tập giá trị của hàm số $y = 2\cos{x} + 1$ $y = 2\cos{x} + 1$.

Trả lời:

$y = 2\cos{x} + 1$ $y = 2\cos{x} + 1$

Ta có: $\ – \ 1 \leq \cos{x} \leq 1$ $\ – \ 1 \leq \cos{x} \leq 1$

$\Rightarrow \ – \ 2 \leq 2\cos{x} \leq 2$ $\Rightarrow \ – \ 2 \leq 2\cos{x} \leq 2$

$\Rightarrow \ – \ 2 + 1 \leq 2\cos{x} + 1 \leq 2 + 1$ $\Rightarrow \ – \ 2 + 1 \leq 2\cos{x} + 1 \leq 2 + 1$ hay $\ – \ 1 \leq y \leq 3$ $\ – \ 1 \leq y \leq 3$

Vậy tập giá trị của hàm số là $[\ – \ 1; 3]$ $[\ – \ 1; 3]$

Bài 4

Dựa vào đồ thị của hàm số $y = \sin{x}$ $y = \sin{x}$, xác định các giá trị $x \in [\ – \ \pi; \pi]$ $x \in [\ – \ \pi; \pi]$ thoả mãn $\sin{x} = \displaystyle \frac{1}{2}$ $\sin{x} = \displaystyle \frac{1}{2}$.

Trả lời:

Ta có: $\sin{x} = \displaystyle \frac{1}{2}$ $\sin{x} = \displaystyle \frac{1}{2}$

$\Leftrightarrow x = \displaystyle \frac{\pi}{6} + k\pi, k \in \mathbb{Z}$ $\Leftrightarrow x = \displaystyle \frac{\pi}{6} + k\pi, k \in \mathbb{Z}$

Vì $x \in [\ – \ \pi; \pi]$ $x \in [\ – \ \pi; \pi]$ nên chọn $k \in \{ \ – \ 1; 0 \}$ $k \in \{ \ – \ 1; 0 \}$

Với $k = \ – \ 1 \Rightarrow x = \displaystyle \frac{\pi}{6} \ – \ \pi = \ – \ \displaystyle \frac{5\pi}{6}$ $k = \ – \ 1 \Rightarrow x = \displaystyle \frac{\pi}{6} \ – \ \pi = \ – \ \displaystyle \frac{5\pi}{6}$

$\Rightarrow \sin{\left(\ – \ \displaystyle \frac{5\pi}{6}\right)} = \displaystyle \frac{1}{2}$ $\Rightarrow \sin{\left(\ – \ \displaystyle \frac{5\pi}{6}\right)} = \displaystyle \frac{1}{2}$ thỏa mãn.

Với $k = 0 \Rightarrow x = \displaystyle \frac{\pi}{6}$ $k = 0 \Rightarrow x = \displaystyle \frac{\pi}{6}$

$\Rightarrow \sin{\displaystyle \frac{\pi}{6}} = \displaystyle \frac{1}{2}$ $\Rightarrow \sin{\displaystyle \frac{\pi}{6}} = \displaystyle \frac{1}{2}$ thỏa mãn.

Vậy $x \in \{\ – \ \displaystyle \frac{5\pi}{6}; \displaystyle \frac{\pi}{6}\}$ $x \in \{\ – \ \displaystyle \frac{5\pi}{6}; \displaystyle \frac{\pi}{6}\}$ thì $\sin{x} = \displaystyle \frac{1}{2}$ $\sin{x} = \displaystyle \frac{1}{2}$

Bài 5

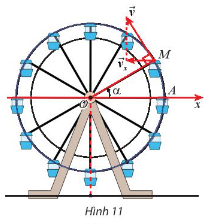
Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin $M$ phụ thuộc vào góc lượng giác $\alpha = (Ox, OM)$ $\alpha = (Ox, OM)$ theo hàm số $v_x = 0,3 \sin{\alpha}$ $v_x = 0,3 \sin{\alpha}$ (m/s) (Hình $11$).$a)$ Tìm giá trị lớn nhất và giá trị nhỏ nhất của $v_x$.$b)$ Dựa vào đồ thị của hàm số $\sin$ $\sin$, hãy cho biết trong vòng quay đầu tiên ( $0 \leq \alpha \leq 2\pi$ $0 \leq \alpha \leq 2\pi$), góc $\alpha$ $\alpha$ ở trong các khoảng nào thì $v_x$ tăng.

Trả lời:

$a)$ Với mọi $\alpha$ $\alpha$ ta có:

$\ – \ 1 \leq \sin{\alpha} \leq 1$ $\ – \ 1 \leq \sin{\alpha} \leq 1$

$\Rightarrow \ – \ 0,3 \leq 0,3\sin{\alpha} \leq 0,3$ $\Rightarrow \ – \ 0,3 \leq 0,3\sin{\alpha} \leq 0,3$

$\Rightarrow \ – \ 0,3 \leq v_x \leq 0,3$ $\Rightarrow \ – \ 0,3 \leq v_x \leq 0,3$

Vậy $v_x$ đạt giá trị nhỏ nhất là $\ – \ 0,3$ $\ – \ 0,3$ m/s và đạt giá trị lớn nhất là $0,3$ m/s.

$b)$ Ta có $v_x$ tăng $\Leftrightarrow 0,3 \sin{\alpha}$ $\Leftrightarrow 0,3 \sin{\alpha}$ tăng

$\Leftrightarrow \sin{\alpha}$ $\Leftrightarrow \sin{\alpha}$ tăng

Xét đồ thị hàm số $y = \sin{\alpha}$ $y = \sin{\alpha}$ khi $\alpha \in [0; 2\pi]$ $\alpha \in [0; 2\pi]$ ta thấy:

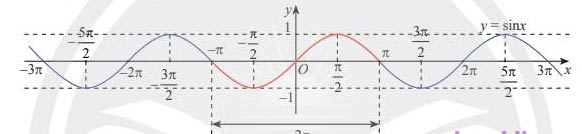
$\sin{\alpha}$ $\sin{\alpha}$ tăng $\Leftrightarrow \alpha \in \left[0; \displaystyle \frac{\pi}{2}\right] \cup \left[\displaystyle \frac{3\pi}{2}; 2\pi \right]$ $\Leftrightarrow \alpha \in \left[0; \displaystyle \frac{\pi}{2}\right] \cup \left[\displaystyle \frac{3\pi}{2}; 2\pi \right]$

Vậy trong vòng quay đầu tiên, khi $\alpha \in \left[0; \displaystyle \frac{\pi}{2}\right] \cup \left[\displaystyle \frac{3\pi}{2}; 2\pi\right]$ $\alpha \in \left[0; \displaystyle \frac{\pi}{2}\right] \cup \left[\displaystyle \frac{3\pi}{2}; 2\pi\right]$ thì $v_x$ tăng.

Bài 6

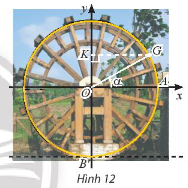
Khoảng cách từ tâm một guồng nước đến mặt nước và bán kính của guồng đều bằng $3$ m. Xét gàu $G$ của guồng. Ban đầu gàu $G$ nằm ở vị trí $A$ (Hình $12$).$a)$ Viết hàm số $h$ biểu diễn chiều cao (tính bằng mét) của gàu $G$ so với mặt nước theo góc $\alpha = (OA, OG)$ $\alpha = (OA, OG)$.$b)$ Guồng nước quay hết mỗi vòng trong $30$ giây. Dựa vào đồ thị của hàm số $\sin$ $\sin$ , hãy cho biết ở các thời điểm $t$ nào trong $1$ phút đầu, khoảng cách của gàu đến mặt nước bằng $1,5$ m.

Trả lời:

$a)$ Gọi $H$ là hình chiếu vuông vuông góc của $G$ lên trục $Ox$

Ta có $GH = OG \sin{\alpha} = 3\sin{\alpha}$ $GH = OG \sin{\alpha} = 3\sin{\alpha}$

Khi đó, chiều cao $h$ của gàu $G$ so với mặt nước là:

$h = 3 + 3\sin{\alpha}$ $h = 3 + 3\sin{\alpha}$ (m)

$b)$ Guồng nước quay mỗi vòng trong $30$ giây tức là cứ $30$ giây, guồng nước quay được một góc là $2\pi$ $2\pi$.

$\Rightarrow$ $\Rightarrow$ Sau $1$ phút đầu, guồng nước quay được góc $4\pi$ $4\pi$

Mỗi giây, guồng nước quay được một góc bằng $\alpha = \displaystyle \frac{2\pi}{30} = \displaystyle \frac{\pi}{15}$ $\alpha = \displaystyle \frac{2\pi}{30} = \displaystyle \frac{\pi}{15}$

Sau $t$ giây, guồng nước quay được góc bằng $\displaystyle \frac{\pi}{15}t$ $\displaystyle \frac{\pi}{15}t$

Khoảng cách của gàu đến mặt nước bằng $1,5$ m khi và chỉ khi $h = 1,5$

$\Leftrightarrow 3 + 3\sin{\alpha} = 1,5$ $\Leftrightarrow 3 + 3\sin{\alpha} = 1,5$

$\Leftrightarrow \sin{\alpha} = \ – \ \displaystyle \frac{1}{2}$ $\Leftrightarrow \sin{\alpha} = \ – \ \displaystyle \frac{1}{2}$

Xét đồ thị hàm số $\sin{\alpha}$ $\sin{\alpha}$ trên khoảng từ $0$ đến $4\pi$ $4\pi$ ta có $\sin{\alpha} = \ – \ \displaystyle \frac{1}{2}$ $\sin{\alpha} = \ – \ \displaystyle \frac{1}{2}$ khi và chỉ khi:

$\alpha \in \{\displaystyle \frac{\pi}{6}; \displaystyle \frac{5\pi}{6}; \displaystyle \frac{3\pi}{2}; \displaystyle \frac{13\pi}{6}\}$ $\alpha \in \{\displaystyle \frac{\pi}{6}; \displaystyle \frac{5\pi}{6}; \displaystyle \frac{3\pi}{2}; \displaystyle \frac{13\pi}{6}\}$

Ta có bảng giá trị sau:

Vậy trong $1$ phút đầu, ở các thời điểm $17,5 s; 27,5s; 47,5s; 57,5s$ thì khoảng cách của gàu đến

Bài 7

Trong Hình $13$, một chiếc máy bay $A$ bay ở độ cao $500$ m theo một đường thẳng đi ngang qua phía trên trạm quan sát $T$ ở mặt đất. Hình chiếu vuông góc của $A$ lên mặt đất là $H$, $\alpha$ $\alpha$ là góc lượng giác $(T_x, TA)$ ( $0 < \alpha < \pi$ $0 < \alpha < \pi$).

$a)$ Biểu diễn toạ độ $x_H$ của điểm $H$ trên trục $T_x$ theo $\alpha$ $\alpha$.$b)$ Dựa vào đồ thị hàm số côtang, hãy cho biết với $\displaystyle \frac{\pi}{6} < \alpha < \displaystyle \frac{2\pi}{3}$ $\displaystyle \frac{\pi}{6} < \alpha < \displaystyle \frac{2\pi}{3}$ thì $x_H$ nằm trong khoảng nào. Làm tròn kết quả đến hàng phần mười.

Trả lời:

$a)$ Chọn hệ trục toạ độ như hình vẽ sao cho gốc toạ độ $O$ trùng với điểm $T$.

Xét tam giác $AHO$ vuông tại $H$ ta có:

$\cot{\alpha} = \displaystyle \frac{OH}{AH} = \displaystyle \frac{OH}{500}$ $\cot{\alpha} = \displaystyle \frac{OH}{AH} = \displaystyle \frac{OH}{500}$ (Vì $0 < \alpha < \pi \text{ nên } \cot{\alpha}$ $0 < \alpha < \pi \text{ nên } \cot{\alpha}$ xác định)

$\Rightarrow OH = 500 \cot{\alpha}$ $\Rightarrow OH = 500 \cot{\alpha}$

Khi đó, toạ độ $x_H$ của điểm $H$ trên trục $T_x$ là: $x_H = 500 \cot{\alpha}$ $x_H = 500 \cot{\alpha}$

$b)$ Xét đồ thị hàm số $\cot{x}$ $\cot{x}$

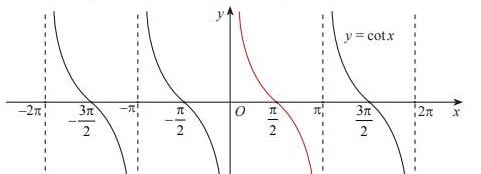
Ta thấy đồ thị hàm số nghịch biến trên khoảng $(0; \pi)$ $(0; \pi)$

Mà $\left(\displaystyle \frac{\pi}{6}; \displaystyle \frac{2\pi}{3}\right) \subset (0; \pi)$ $\left(\displaystyle \frac{\pi}{6}; \displaystyle \frac{2\pi}{3}\right) \subset (0; \pi)$

$\Rightarrow \cot{\alpha} \in \left(\ – \ \displaystyle \frac{\sqrt{3}}{3}; \sqrt{3}\right)$ $\Rightarrow \cot{\alpha} \in \left(\ – \ \displaystyle \frac{\sqrt{3}}{3}; \sqrt{3}\right)$

Suy ra $x_H = 500 \cot{\alpha} \in (\ – \ 288,7; 866)$ $x_H = 500 \cot{\alpha} \in (\ – \ 288,7; 866)$

Vậy khi $\displaystyle \frac{\pi}{6} < \alpha < \displaystyle \frac{2\pi}{3}$ $\displaystyle \frac{\pi}{6} < \alpha < \displaystyle \frac{2\pi}{3}$ thì $x_H$ thuộc khoảng $(\ – \ 288,7 m; 866 m)$ $(\ – \ 288,7 m; 866 m)$