Toán 7 Bài 9: Tính chất ba đường phân giác của tam giác Giải Toán lớp 7 trang 79 sách Chân trời sáng tạo - Tập 2

Giải bài tập SGK Toán 7 Tập 2 trang 79, 80, 81, 82 sách Chân trời sáng tạo giúp các em học sinh lớp 7 xem gợi ý giải các bài tập của Bài 9: Tính chất ba đường phân giác của tam giác.

Thông qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 9 Chương 8 - Tam giác trong sách giáo khoa Toán 7 Tập 2 Chân trời sáng tạo. Đồng thời, cũng giúp thầy cô tham khảo để soạn giáo án cho học sinh của mình theo chương trình mới. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 7 Chân trời sáng tạo trang 81, 82 tập 2

Bài 1

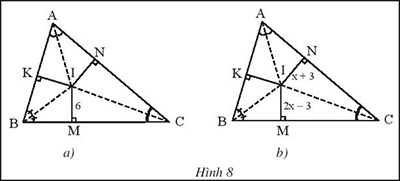
Trong hình 8, I là giao điểm ba đường phân giác của tam giác ABC.

a) Cho biết IM = 6 (Hình 8a). Tính IK và IN.

b) Cho biết IN = x + 3, IM = 2x -3 (Hình 8b). Tìm x.

Gợi ý đáp án:

a) I là giao điểm của ba đường phân giác của tam giác ABC

=> IM = IN =IK

mà IM = 6

=> IN = IK = 6.

b) I là giao điểm của ba đường phân giác của tam giác ABC.

=> IM = IN

=> 2x - 3 = x + 3

<=> x = 6.

Vậy x = 6.

Bài 2

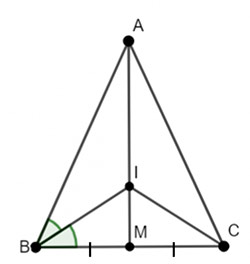
Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. Tia phân giác của góc B cắt AM tại I. Chứng minh rằng CI là tia phân giác của góc C.

Gợi ý đáp án:

+ Xét \(\triangle ABM\) và \(\triangle ACM\) có:

AB = AC (tam giác cân tại A)

BM = CM (M là trung điểm BC)

AM chung

\(\Rightarrow \triangle ABM = \triangle ACM (c.c.c)\)

\(\Rightarrow AM\) là tia phân giác của tam giác ABC.

+ Xét tam giác ABC có: BI và AM là hai tia phân giác.

Mà BI và AM cắt nhau tại I

\(\Rightarrow\) I là giao của ba đường phân giác trong tam giác ABC.

\(\Rightarrow\) CI là tia phân giác của góc C.

Bài 3

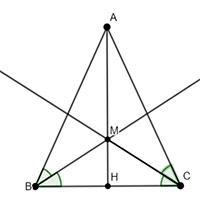
Cho tam giác ABC cân tại A. Tia phân giác của các góc B và C cắt nhau tại M. Tia AM cắt BC tại H. Chứng minh H là trung điểm của BC.

Gợi ý đáp án:

M là giao điểm của 2 tia phân giác của \(\widehat{ABC}\) và \(\widehat{ACB}\) trong ∆ABC

=> AM là phân giác của \(\widehat{BAC}\)

\(=> \widehat{BAM} = \widehat{CAM}\)

+ Xét ∆ ABH và ∆ ACH có

AB = AC

\(\widehat{BAH} = \widehat{CAH}\)

AH chung

=> ∆ABH = ∆ACH (c.g.c)

=> HB = HC

=> H là trung điểm của BC.

Bài 4

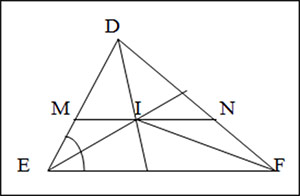
Cho tam giác DEF. Tia phân giác của góc D và E cắt nhau tại I. Qua I kẻ đường thẳng song song với EF, đường thẳng này cắt DE tại M, cắt DF tại N. Chứng minh rằng ME + NF = MN.

Gợi ý đáp án:

+ \(MN // EF => MI // EF => \widehat{MIE} = \widehat{IEF}\) (2 góc so le trong)

Mà \(\widehat{MEI} = \widehat{IEF}\)(EI là đường phân giác của \(\widehat{DEF}\))

\(=>\widehat{MEI} = \widehat{MIE}\)

=> ∆MEI cân tại M

=> ME = MI.

+ IF là đường phân giác của \(\widehat{DFE} => \widehat{NFI} = \widehat{IFE}\)

\(IN // EF => \widehat{NIF}= \widehat{IFE}\) (hai góc so le trong)

\(=> \widehat{NFI} = \widehat{NIF}\)

=> ∆ NIF cân tại N => NI = NF

+ Có MI + NI = MN; MI = ME; NI = NF

=> ME + NF = MN.

Bài 5

Cho tam giác ANM vuông tại A. Tia phân giác của góc M và N cắt nhau tại I. Tia MI cắt AN tại R. Kẻ RT vuông góc với AI tại T. Chứng minh rằng AT = RT.

Gợi ý đáp án:

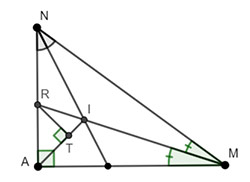
+ Xét ∆AMN có: I là giao điểm của hai đường phân giác của góc \(\widehat{ANM}\) và góc \(\widehat{AMN}\)

=> AI là tia phân giác của \(\widehat{NAM}\) trong tam giác AMN.

\(=> \widehat{IAN}= \widehat{IAM} = \frac{1}{2} \widehat{NAM} = \frac{1}{2} 90°= 45°\)

+ Xét ∆ART vuông tại T

\(=> \widehat{TRA} = 90° - 45°= 45°\)

\(=> \widehat{TRA} = \widehat{TAR}\)

=> ∆ART vuông cân tại T.

=> AT = RT.

Bài 6

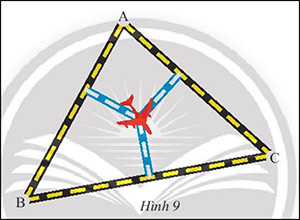
Ba thành phố A, B, C được nối với nhau bởi ba xa lộ (Hình 9). Người ta muốn tìm một địa điểm để làm một sân bay sao cho địa điểm này phải cách đều ba xa lộ đó. Hãy xác định vị trí của sân bay thảo mãn điều kiện trên và giải thích cách thực hiện

Gợi ý đáp án: