Toán 7 Bài 7: Tính chất ba đường trung tuyến của tam giác Giải Toán lớp 7 trang 73 sách Chân trời sáng tạo - Tập 2

Giải bài tập SGK Toán 7 Tập 2 trang 73, 74, 75, 76 sách Chân trời sáng tạo giúp các em học sinh lớp 7 xem gợi ý giải các bài tập của Bài 7: Tính chất ba đường trung tuyến của tam giác.

Thông qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 7 Chương 8 - Tam giác trong sách giáo khoa Toán 7 Tập 2 Chân trời sáng tạo. Đồng thời, cũng giúp thầy cô tham khảo để soạn giáo án cho học sinh của mình theo chương trình mới. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 7 Chân trời sáng tạo trang 75, 76 tập 2

Bài 1

Quan sát Hình 8. Thay ? bằng số thích hợp

EG = ..?... EM , GM = ..?.. EM, GM = ..?.. EG, FG = ..?.. GN, FN = ..?.. GN, FN = ..?.. FG

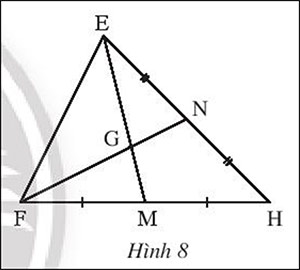
Gợi ý đáp án:

Ta thay như sau:

\(EG = \frac{2}{3} EM\)

\(GM = \frac{1}{3} EM\)

\(GM = \frac{1}{2} GE\)

\(FG = 2GN\)

\(FN = 3GN\)

\(FN = \frac{3}{2} FG\)

Bài 2

Quan sát hình 9

a) Biết AM = 15 cm, tính AG

b) Biết GN = 6 cm, tính CN

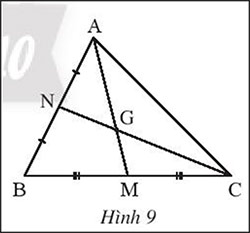
Gợi ý đáp án:

Trong tam giác ABC có AM, NC là hai đường trung tuyến

G là giao điểm của AM, NC

=> G là trọng tâm của tam giác ABC

a) \(AG = \frac{2}{3} AM\)

\(=> AG = \frac{2}{3}. 15\)

=> AG = 10

b) \(GN = \frac{1}{3}.CN\)

\(=> 6 = \frac{1}{3}.CN\)

=> CN = 6. 3 = 18

Bài 3

Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia AM lấy điểm E sao cho ME = MG.

a) Chứng minh rằng BG song song với EC.

b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh AF = 2 FI.

Gợi ý đáp án:

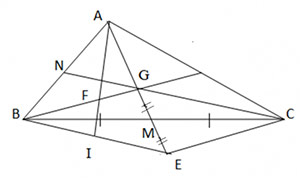
a) Xét ∆BMG và ∆CME ta có:

BM = CM (M là trung điểm của BC)

\(\widehat{BMG} = \widehat{CME}\)(hai góc đối đỉnh)

ME = MG (giả thiết)

=> ∆ BMG = ∆ CME (c.g.c)

\(=> \widehat{GBM} = \widehat{BCE}\);

Mà hai góc ở vị trị so le trong

=> GB // CE.

b) Xét tam giác ABC có AM và CN là hai đường trung tuyến cắt nhau tại G

=> G là trọng tâm của tam giác ABC

=> AG = 2GM

+ Ta có: GE = GM + EM

=> GE = 2GM (GM = EM)

=> AG = GE

=> G là trung điểm đoạn thẳng AE

=> BG là đường trung tuyến của tam giác ABM.

+ Xét tam giác ABM có: AI và BG là 2 đường trung tuyến

mà AI cắt BG tại F

=> F là trọng tâm của tam giác ABC

=> AF = 2FI.

Bài 4

Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.

a) Chứng minh rằng BM = CN.

b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm BC.

Gợi ý đáp án:

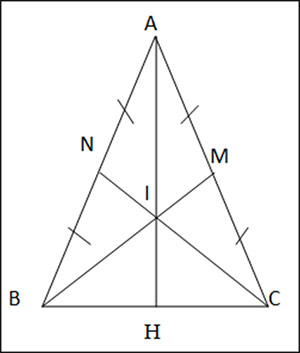
a) ∆ ABC cân tại A

=> AB = AC

N là trung điểm của \(AB => AN = NB = \frac{1}{2} AB\)

M là trung điểm của \(AC => AM = MC = \frac{1}{2} AC\)

=> AN = AM

Xét ∆ ANC và ∆ AMB ta có:

AB = AC

\(\widehat{BAC}\) chung

AN = AM

=> ∆ ANC = ∆ AMB (c.g.c)

=> NC = MB

b) 2 đường trung tuyến BM và CN cắt nhau tại I

=> I là trọng tâm của ∆ ABC

\(=> IB = \frac{2}{3} BM, IC = \frac{1}{2} CN\)

Mà BM = CN

=> IB = IC

+ Xét ∆ ACI và ∆ ABI có:

AB = AC

AI chung

IB = IC

=> ∆ ACI = ∆ ABI (c.c.c)

\(=> \widehat{BAI} = \widehat{CAI}\)

+ Xét ∆ ABH và ∆ ACH có:

AB = AC

\(\widehat{BAH} = \widehat{CAH}\)

AH chung

=> ∆ ABH = ∆ ACH (c.g.c).

=> BH = CH

=> H là trung điểm của BC.

Bài 5

Cho tam giác ABC có đường trung tuyến BM bằng đường trung tuyến CN. Chứng minh rằng tam giác ABC cân

Gợi ý đáp án:

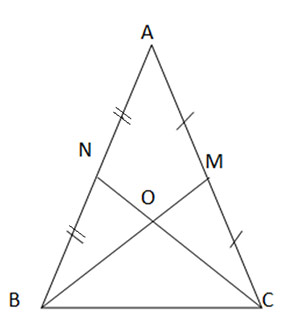
Gọi O là giao điểm của BM và CN

=> O là trọng tâm của tam giác ABC

\(=> CO =\frac{2}{3} CN, BO = \frac{2}{3} BM\)

Mà BM = CN

=> CO = BO

=> ∆ OBC cân tại O

\(=> \widehat{OBC} = \widehat{OCB}\)

Hay \(\widehat{MBC} = \widehat{NCB}\)

Xét ∆ NBC và ∆ MBC ta có:

CN = BM

\(\widehat{MBC} = \widehat{NCB}\)

BC chung

=> ∆ NBC = ∆ MBC (c.g.c)

\(=> \widehat{MCB} = \widehat{NBC}\)

Hay \(\widehat{ACB} = \widehat{ABC}\)

=> ∆ ABC cân tại A.

Bài 6

Cho tam giác ABC cân tại A có BE và CD là hai đường trung tuyến cắt nhau tại F (Hình 10). Biết BE = 9 cm, tính độ dài đoạn thẳng DF

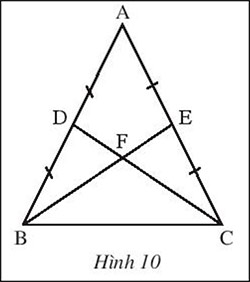
Gợi ý đáp án:

+ ∆ ABC cân tại A

=> AB = AC

D là trung điểm của\(AB => AD = \frac{1}{2}AB\)

E là trung điểm của \(AC => AE = \frac{1}{2}AC\)

=> AD = AE

+ Xét ∆ ABE và ∆ ACD có:

AB = AC

\(\widehat{A}\) chung

AE = AD

=> ∆ ABE = ∆ ACD (c.g.c)

=> BE = CD = 9cm

+ Xét ∆ ABC có hai đường trung tuyến BE và CD cắt nhau tại F

=> F là trọng tâm của tam giác ABC

\(=> DF = \frac{1}{3} DC\)

\(=> DF = \frac{1}{3}.9 = 3 cm\)