Toán 7 Bài 2: Các phép tính với số hữu tỉ Giải Toán lớp 7 trang 11 sách Chân trời sáng tạo - Tập 1

Giải bài tập Toán lớp 7 Bài 2: Các phép tính với số hữu tỉ với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 7 Tập 1 Chân trời sáng tạo trang 11, 12, 13, 14, 15, 16, 17. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 7 Bài 2 chi tiết phần câu hỏi, luyện tập, bài tập, đồng thời còn giúp các em hệ thống lại toàn bộ kiến thức lý thuyết trọng tâm của Bài 2 Chương I: Số hữu tỉ. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Phần Hoạt động

Hoạt động 1 trang 11 Toán 7 tập 1

Từ mặt nước biển, một thiết bị lặn khảo sát lặn xuống \(\frac{{43}}{6}\)m. Sau đó nó tiếp tục lặn xuống thêm 5,4m nữa. Hỏi khi đó thiết bị lặn ở độ cao bao nhiêu mét so với mực nước biển?

Hướng dẫn giải

Thiết bị lặn ở độ cao so với mực nước biển là:

\(\frac{{43}}{6} + 5,4 = \frac{{43}}{6} + \frac{{54}}{{10}} = \frac{{215}}{{30}} + \frac{{162}}{{30}} = \frac{{377}}{{30}}\left( m \right)\)

Vậy khi đó thiết bị lặn ở độ cao \(\frac{{377}}{{30}}\)mét so với mực nước biển

Hoạt động 2 trang 12 Toán 7 tập 1

Cho biểu thức: \(M = \frac{1}{2} + \frac{2}{3} + \left( { - \frac{1}{2}} \right) + \frac{1}{3}\). Hãy tính giá trị của M theo hai cách:

a) Thực hiện phép tính từ trái sang phải.

b) Nhóm các số hạng thích hợp rồi thực hiện phép tính.

Hướng dẫn giải

a) Thực hiện phép tính từ trái sang phải như sau:

\(\begin{matrix} M = \dfrac{1}{2} + \dfrac{2}{3} + \left( { - \dfrac{1}{2}} \right) + \dfrac{1}{3} \hfill \\ M = \dfrac{3}{6} + \dfrac{4}{6} + \left( { - \dfrac{3}{6}} \right) + \dfrac{2}{6} \hfill \\ M = \dfrac{{3 + 4 + \left( { - 3} \right) + 2}}{6} = \dfrac{6}{6} = 1 \hfill \\ \end{matrix}\)

b) Nhóm các số hạng thích hợp rồi thực hiện phép tính như sau:

\(M = \frac{1}{2} + \frac{2}{3} + \left( { - \frac{1}{2}} \right) + \frac{1}{3}\)

\(M = \frac{1}{2} + \left( { - \frac{1}{2}} \right) + \frac{2}{3} + \frac{1}{3}\) ---> Tính chất giao hoán

\(M = \left[ {\frac{1}{2} + \left( { - \frac{1}{2}} \right)} \right] + \left[ {\frac{2}{3} + \frac{1}{3}} \right]\) ----> Tính chất kết hợp

\(M = 0 + 1 = 1\) -----> Tính chất cộng với số 0

Phần Thực hành

Thực hành 1 trang 11 Toán 7 tập 1

Tính:

Gợi ý đáp án:

a) \(0,6 + \left( {\frac{3}{{ - 4}}} \right) = \frac{6}{{10}} + \frac{{ - 3}}{4} = \frac{{12}}{{20}} + \frac{{ - 15}}{{20}} = \frac{{ - 3}}{{20}}\)

b) \(\left( { - 1\frac{1}{3}} \right) - \left( { - 0,8} \right) = \frac{{ - 4}}{3} + \frac{8}{{10}} = \frac{{ - 40}}{{30}} + \frac{{24}}{{30}} = \frac{{ - 16}}{{30}} = \frac{{ - 8}}{{15}}\)

Thực hành 2 trang 11 Toán 7 tập 1

Nhiệt độ hiện tại trong một kho lạnh là -5,8 ⁰ C. Do yêu cầu bảo quản hàng hóa, người quản lí kho tiếp tục giảm độ lạnh của kho thêm \(\frac{5}{2}\) ⁰ C nữa. Hỏi khi đó nhiệt độ trong kho là bao nhiêu độ?

Gợi ý đáp án:

Nhiệt độ trong kho khi đó là:

\(- 5,8 - \frac{5}{2} = \frac{{ - 58}}{{10}} - \frac{5}{2} = \frac{{ - 58}}{{10}} - \frac{{25}}{{10}} = \frac{{ - 83}}{{10}} = - 8,{3^0}C\)

Vậy nhiệt độ trong kho là -8,3⁰C

Thực hành 3 trang 12 Toán 7 tập 1

Tính giá trị của biểu thức sau một cách hợp lí:

\(B = \left( {\frac{{ - 3}}{{13}}} \right) + \frac{{16}}{{23}} + \left( {\frac{{ - 10}}{{13}}} \right) + \frac{5}{{11}} + \frac{7}{{23}}\)

Gợi ý đáp án:

Thực hiện phép tính như sau:

\(B = \left( {\frac{{ - 3}}{{13}}} \right) + \frac{{16}}{{23}} + \left( {\frac{{ - 10}}{{13}}} \right) + \frac{5}{{11}} + \frac{7}{{23}}\)

\(B = \left[ {\left( {\frac{{ - 3}}{{13}}} \right) + \left( {\frac{{ - 10}}{{13}}} \right)} \right] + \left[ {\frac{7}{{23}} + \frac{{16}}{{23}}} \right] + \frac{5}{{11}}\)

\(B = \frac{{ - 13}}{{13}} + \frac{{23}}{{23}} + \frac{5}{{11}}\)

\(B = - 1 + 1 + \frac{5}{{11}} = \frac{5}{{11}}\)

Thực hành 4 trang 13 Toán 7 tập 1

Tính:

Gợi ý đáp án:

Thực hiện phép tính như sau:

Thực hành 5 trang 14 Toán 7 tập 1

Tính:

Gợi ý đáp án:

Thực hiện phép tính như sau:

Thực hành 6 trang 15 Toán 7 tập 1

Tính:

Gợi ý đáp án:

Thực hiện phép tính như sau:

a) \(\frac{{14}}{{15}}:\left( { - \frac{7}{5}} \right) = \frac{{14}}{{15}}.\frac{{ - 5}}{7} = \frac{{ - 2}}{3}\)

b) \(\left( { - 2\frac{2}{5}} \right):\left( { - 0,32} \right) = \left( { - \frac{{12}}{5}} \right):\left( { - \frac{{32}}{{100}}} \right)\)

\(= \left( {\frac{{ - 12}}{5}} \right):\left( { - \frac{8}{{25}}} \right) = \left( {\frac{{ - 12}}{5}} \right).\left( {\frac{{ - 25}}{8}} \right) = - \frac{{15}}{2}\)

Thực hành 7 trang 15 Toán 7 tập 1

Một căn phòng hình chữ nhật có chiều rộng là \(\frac{{15}}{4}\) m, chiều dài là \(\frac{{27}}{5}\) m. Tính tỉ số giữa chiều dài và chiều rộng của căn phòng đó.

Gợi ý đáp án:

Tỉ số giữa chiều dài và chiều rộng của căn phòng là:

\(\frac{{27}}{5}:\frac{{15}}{4} = \frac{{27}}{5}.\frac{4}{{15}} = \frac{{36}}{{25}}\)

Phần Bài tập

Bài 1 trang 16 Toán 7 tập 1

Tính:

Gợi ý đáp án:

Thực hiện các phép tính như sau:

Bài 2 trang 16 Toán 7 tập 1

Tính:

Gợi ý đáp án:

Thực hiện các phép tính như sau:

a) \(0,75 - \frac{5}{6} + 1\frac{1}{2}\)

\(= \frac{3}{4} - \frac{5}{6} + \frac{3}{2} = \frac{9}{{12}} - \frac{{10}}{{12}} + \frac{{18}}{{12}} = \frac{{17}}{{12}}\)

b) \(\frac{3}{7} + \frac{4}{{15}} + \left( {\frac{{ - 8}}{{21}}} \right) + \left( { - 0,4} \right)\)

\(\begin{matrix} = \dfrac{3}{7} + \dfrac{4}{{15}} + \left( {\dfrac{{ - 8}}{{21}}} \right) - \dfrac{2}{5} \hfill \\ = \left[ {\dfrac{3}{7} + \left( {\dfrac{{ - 8}}{{21}}} \right)} \right] + \left[ {\dfrac{4}{{15}} - \dfrac{2}{5}} \right] \hfill \\ \end{matrix}\)

\(\begin{matrix} = \left[ {\dfrac{9}{{21}} + \left( {\dfrac{{ - 8}}{{21}}} \right)} \right] + \left[ {\dfrac{4}{{15}} - \dfrac{6}{{15}}} \right] \hfill \\ = \dfrac{1}{{21}} - \dfrac{2}{{15}} = \dfrac{5}{{105}} - \dfrac{{14}}{{105}} = \dfrac{{ - 9}}{{105}} = \dfrac{{ - 3}}{{105}} \hfill \\ \end{matrix}\)

c) \(0,625 + \left( {\frac{{ - 2}}{7}} \right) + \frac{3}{8} + \left( {\frac{{ - 5}}{7}} \right) + 1\frac{2}{3}\)

\(\begin{matrix} = \dfrac{5}{8} + \left( {\dfrac{{ - 2}}{7}} \right) + \dfrac{3}{8} + \left( {\dfrac{{ - 5}}{7}} \right) + \dfrac{5}{3} \hfill \\ = \left[ {\dfrac{5}{8} + \dfrac{3}{8}} \right] + \left[ {\left( {\dfrac{{ - 2}}{7}} \right) + \left( {\dfrac{{ - 5}}{7}} \right)} \right] + \dfrac{5}{3} \hfill \\ = 1 + \left( { - 1} \right) + \dfrac{5}{3} = \dfrac{5}{3} \hfill \\ \end{matrix}\)

d) \(\left( { - 3} \right).\left( {\frac{{ - 38}}{{21}}} \right).\left( {\frac{{ - 7}}{6}} \right).\left( { - \frac{3}{{19}}} \right)\)

\(\begin{matrix} = \dfrac{{\left( { - 3} \right).\left( { - 38} \right).\left( { - 7} \right).\left( { - 3} \right)}}{{21.6.19}} \hfill \\ = \dfrac{{3.7.2.19.3}}{{3.7.2.3.19}} = 1 \hfill \\ \end{matrix}\)

e) \(\left( {\frac{{11}}{{18}}:\frac{{22}}{9}} \right).\frac{8}{5}\)

\(= \frac{{11}}{{18}}.\frac{9}{{22}}.\frac{8}{5} = \frac{{11.9.8}}{{18.22.5}} = \frac{{11.9.2.4}}{{2.9.11.2.5}} = \frac{2}{5}\)

g) \(\left[ {\left( {\frac{{ - 4}}{5}} \right).\frac{5}{8}} \right]:\left( {\frac{{ - 25}}{{12}}} \right)\)

\(= \frac{{ - 1}}{2}.\frac{{12}}{{ - 25}} = \frac{6}{{25}}\)

Bài 3 trang 16 Toán 7 tập 1

Thay ? bằng dấu (>, < , =) thích hợp:

Gợi ý đáp án:

a) \(\left( {\frac{{ - 5}}{8}} \right) + \left( {\frac{3}{{ - 8}}} \right){\text{ ? - 1}}\)

Ta có:

\(\left( {\frac{{ - 5}}{8}} \right) + \left( {\frac{3}{{ - 8}}} \right) = \left( {\frac{{ - 5}}{8}} \right) + \left( {\frac{{ - 3}}{8}} \right) = \frac{{\left( { - 5} \right) + \left( { - 3} \right)}}{8} = \frac{{ - 8}}{8} = - 1\)

Vậy dầu cần điền là dấu “=”

b) \(\left( {\frac{{ - 13}}{{22}}} \right) + \left( {\frac{{ - 5}}{{22}}} \right){\text{ ? }}\frac{{ - 8}}{{11}}\)

Ta có:

\(\left( {\frac{{ - 13}}{{22}}} \right) + \left( {\frac{{ - 5}}{{22}}} \right) = \frac{{\left( { - 13} \right) + \left( { - 5} \right)}}{{22}} = \frac{{ - 18}}{{22}} = \frac{{ - 9}}{{11}}\)

Ta có: -9 < -8 => \(\frac{{ - 9}}{{11}} < \frac{{ - 8}}{{11}}\)

Vậy dấu cần điền là “ < “

c) \(\frac{1}{6} + \left( {\frac{{ - 3}}{4}} \right){\text{ ? }}\frac{1}{{14}} + \left( {\frac{{ - 4}}{7}} \right)\)

Ta có:

\(\begin{matrix} \dfrac{1}{6} + \left( {\dfrac{{ - 3}}{4}} \right) = \dfrac{2}{{12}} + \left( {\dfrac{{ - 9}}{{12}}} \right) = \dfrac{{ - 7}}{{12}} \hfill \\ \dfrac{1}{{14}} + \left( {\dfrac{{ - 4}}{7}} \right) = \dfrac{1}{{14}} + \dfrac{{ - 8}}{{14}} = \dfrac{{ - 7}}{{14}} \hfill \\ \end{matrix}\)

Mặt khác \(\frac{{ - 7}}{{12}} < \frac{{ - 7}}{{14}}\)

Vậy dấu cần điền là: “<”

Bài 4 trang 16 Toán 7 tập 1

Tính:

Gợi ý đáp án:

Thực hiện các phép tính như sau:

a) \(\frac{3}{7}.\left( { - \frac{1}{9}} \right) + \frac{3}{7}.\left( { - \frac{2}{3}} \right)\)

\(\begin{matrix} = \dfrac{3}{7}.\left[ {\left( { - \dfrac{1}{9}} \right) + \left( { - \dfrac{2}{3}} \right)} \right] \hfill \\ = \dfrac{3}{7}.\left[ {\left( { - \dfrac{1}{9}} \right) + \left( { - \dfrac{6}{9}} \right)} \right] \hfill \\ = \dfrac{3}{7}.\dfrac{{ - 7}}{9} = \dfrac{{ - 1}}{3} \hfill \\ \end{matrix}\)

b) \(\left( {\frac{{ - 7}}{{13}}} \right).\frac{5}{{12}} + \left( {\frac{{ - 7}}{{13}}} \right).\frac{7}{{12}} + \left( {\frac{{ - 6}}{{13}}} \right)\)

\(\begin{matrix} = \left( {\dfrac{{ - 7}}{{13}}} \right).\left( {\dfrac{5}{{12}} + \dfrac{7}{{12}}} \right) + \left( {\dfrac{{ - 6}}{{13}}} \right) \hfill \\ = \left( {\dfrac{{ - 7}}{{13}}} \right).\left( {\dfrac{{12}}{{12}}} \right) + \left( {\dfrac{{ - 6}}{{13}}} \right) \hfill \\ = \left( {\dfrac{{ - 7}}{{13}}} \right).1 + \left( {\dfrac{{ - 6}}{{13}}} \right) = \left( {\dfrac{{ - 7}}{{13}}} \right) + \left( {\dfrac{{ - 6}}{{13}}} \right) = \dfrac{{ - 13}}{{13}} = - 1 \hfill \\ \end{matrix}\)

c) \(\left[ {\left( {\frac{{ - 2}}{3}} \right) + \frac{3}{7}} \right]:\frac{5}{9} + \left( {\frac{4}{7} - \frac{1}{3}} \right):\frac{5}{9}\)

\(\begin{matrix} = \left[ {\left( {\dfrac{{ - 2}}{3}} \right) + \dfrac{3}{7}} \right].\dfrac{9}{5} + \left( {\dfrac{4}{7} - \dfrac{1}{3}} \right).\dfrac{9}{5} \hfill \\ = \dfrac{{ - 5}}{{21}}.\dfrac{9}{5} + \dfrac{5}{{21}}.\dfrac{9}{5} = 0 \hfill \\ \end{matrix}\)

d) \(\frac{5}{9}:\left( {\frac{1}{{11}} - \frac{5}{{22}}} \right) + \frac{5}{9}:\left( {\frac{1}{{15}} - \frac{2}{3}} \right)\)

\(\begin{matrix} = \dfrac{5}{9}:\left( {\dfrac{{ - 3}}{{22}}} \right) + \dfrac{5}{9}:\left( {\dfrac{{ - 3}}{5}} \right) \hfill \\ = \dfrac{5}{9}.\dfrac{{22}}{{ - 3}} + \dfrac{5}{9}.\dfrac{5}{{ - 3}} \hfill \\ = \dfrac{5}{9}.\left[ {\dfrac{{22}}{{ - 3}} + \dfrac{5}{{ - 3}}} \right] \hfill \\ = \dfrac{5}{9}.\dfrac{{ - 27}}{3} = - 5 \hfill \\ \end{matrix}\)

e) \(\frac{3}{5} + \frac{3}{{11}} - \left( {\frac{{ - 3}}{7}} \right) + \left( {\frac{{ - 2}}{{97}}} \right) - \frac{1}{{35}} - \frac{3}{4} + \left( {\frac{{ - 23}}{{44}}} \right)\)

\(\begin{matrix} = \left[ {\dfrac{3}{5} - \left( {\dfrac{{ - 3}}{7}} \right) - \dfrac{1}{{35}}} \right] + \left[ { - \dfrac{3}{4} + \dfrac{3}{{11}} + \left( {\dfrac{{ - 23}}{{44}}} \right)} \right] + \left( {\dfrac{{ - 2}}{{97}}} \right) \hfill \\ = \left[ {\dfrac{{21}}{{35}} - \left( {\dfrac{{ - 15}}{{35}}} \right) - \dfrac{1}{{35}}} \right] + \left[ { - \dfrac{{33}}{{44}} + \dfrac{{12}}{{44}} + \left( {\dfrac{{ - 23}}{{44}}} \right)} \right] + \left( {\dfrac{{ - 2}}{{97}}} \right) \hfill \\ = 1 + \left( { - 1} \right) + \left( {\dfrac{{ - 2}}{{97}}} \right) = - \dfrac{2}{{97}} \hfill \\ \end{matrix}\)

Bài 5 trang 16 Toán 7 tập 1

Tìm x, biết:

Gợi ý đáp án:

Bài 6 trang 16 Toán 7 tập 1

Hai đoạn ống nước có chiều dài lần lượt là 0,8m và 1,35m. Người ta nối hai đầu ống để tạo thành một ống nước mới. Chiều dài của phần nối chung là \(\frac{2}{{25}}\) m. Hỏi đoạn ống nước mới dài bao nhiêu mét?

Gợi ý đáp án:

Đoạn ống nước mới dài số mét là:

(0,8 + 1,35) – \(\frac{2}{{25}}\)

\(\begin{matrix} = \dfrac{8}{{10}} + \dfrac{{135}}{{100}} - \dfrac{2}{{25}} \hfill \\ = \dfrac{{80}}{{100}} + \dfrac{{135}}{{100}} - \dfrac{8}{{100}} = \dfrac{{207}}{{100}} \hfill \\ \end{matrix}\)

= 2,07 (m)

Vậy đoạn ống nước mới dài 2,07m.

Bài 7 trang 16 Toán 7 tập 1

Một nhà máy trong tuần đã thực hiện được \(\frac{4}{{15}}\) kế hoạch tháng, trong tuần thứ hai thực hiện được \(\frac{7}{{30}}\) kế hoạch, trong tuần thứ ba thực hiện được \(\frac{3}{{10}}\) kế hoạch. Để hoàn thành kế hoạch của tháng thì trong tuần cuối nhà máy phải thực hiện bao nhiêu phần trăm kế hoạch?

Gợi ý đáp án:

Trong tuần cuối nhà máy phải thực hiện số phần kế hoạch là:

\(\begin{matrix} 1 - \dfrac{4}{{15}} - \dfrac{7}{{30}} - \dfrac{3}{{10}} \hfill \\ = \dfrac{{30}}{{30}} - \dfrac{8}{{30}} - \dfrac{7}{{30}} - \dfrac{9}{{30}} \hfill \\ \end{matrix}\)

\(= \frac{6}{{30}} = \frac{1}{5}\) (kế hoạch)

Số phần kế hoạch tuần cuối nhà máy phải làm chiếm 20% kế hoạch ban đầu.

Bài 8 trang 16 Toán 7 tập 1

Vào tháng 6, giá niêm yết một chiếc tivi 42 inch tại một siêu thị điện máy là 8 000 000 đồng. Đến tháng 9, siêu thị giảm giá 5% cho mỗi chiếc tivi. Sang tháng 10, siêu thị lại giảm giá thêm một lần nữa, lúc này giá một chiếc tivi 42 inch chỉ còn 6 840 000 đồng. Hỏi tháng 10, siêu thị đã giảm giá bao nhiêu phần trăm cho một chiếc tivi cho tháng 9?

Gợi ý đáp án:

Trong tháng 9, chiếc tivi 42 inch được giảm số tiền là:

8000000 . 5% = 400 000 (đồng)

Tháng 9, giá của chiếc tivi 42 inch là:

8 000 000 - 400 000 = 7 600 000 (đồng)

Tháng 10, siêu thị đã giảm giá số phần trăm cho một chiếc tivi cho tháng 9 là:

\(\frac{{7600000 - 6840000}}{{7600000}}.100\% = 10\%\)

Bài 9 trang 16 Toán 7 tập 1

Một cửa hàng sách có chương trình khuyến mãi như sau: Khách hàng có thẻ thành viên sẽ được giảm 10% tổng số tiền của hóa đơn. Bạn Lan có thẻ thành viên và bạn mua 3 quyển sách, mỗi quyển đều có giá 120 000 đồng, Bạn đưa cho cô thu ngân 350 000 đồng. Hỏi bạn Lan được trả lại bao nhiêu tiền?

Gợi ý đáp án:

Số tiền mua 3 quyển sách của bạn Lan (khi chưa giảm giá) là:

120 000 . 3 = 360 000 (đồng)

Số tiền bạn Lan được giảm giá là:

360 000 . 10% = 36 000 (đồng)

=> Số tiền bạn Lan phải trả là:

360 000 – 36 000 = 324 000 (đồng)

=> Số tiền cô thu ngân phải trả cho bạn Lan là:

350 000 – 324 000 = 26 000 (đồng)

Vậy bạn Lan được trả 26 000 đồng.

Bài 10 trang 16 Toán 7 tập 1

Đường kình của Sao Kim bằng \(\frac{6}{25}\) đường kính của Sao Thiên Vương. Đường kính của Sao Thiên Vương bằng \(\frac{5}{{14}}\) đường kính của Sao Mộc.

a) Đường kính của Sao Kim bằng bao nhiêu phần đường kính của Sao Mộc?

b) Biết rằng đường kính của Sao Mộc bằng 140 000km, tính đường kính của Sao Kim?

Gợi ý đáp án:

a) Đường kính của Sao Kim bằng số phần đường kính của Sao Mộc là:

\(\frac{6}{{25}}.\frac{5}{{14}} = \frac{{6.5}}{{25.14}} = \frac{3}{{5.7}} = \frac{3}{{35}}\)

Vậy đường kính của Sao Kim bằng \(\frac{3}{{35}}\) phần đường kính của Sao Mộc.

b) Đường kính của Sao Kim là:

\(140000.\frac{3}{{35}} = \frac{{140000.3}}{{35}} = 12000\left( {km} \right)\)

Vậy Sao Kim có đường kính là 12 000 km.

Bài 11 trang 16 Toán 7 tập 1

Trong tầng đối lưu, nhiệt độ giảm dần theo độ cao. Cứ lên cao 100m thì nhiệt độ không khí giảm khoảng 0,6 ^o C (Theo: Sách giáo khoa Địa lí 6 – 2020 – Nhà xuất bản Giáo dục Việt Nam).

a) Tính nhiệt độ không khí bên ngoài một khinh khí cầu đang bay ở độ cao 2,8 km, biết rằng nhiệt độ trên mặt đất lúc đó là 28^o

b) Nhiệt độ bên ngoài một khinh khí cầu đang bay ở độ cao km bằng -8,5^o Hỏi nhiệt độ trên mặt đất tại vùng trời khinh khí cầu đang bay lúc đó là bao nhiêu độ C?

Gợi ý đáp án:

a) Đổi 2,8 km = 2800 m

Theo bài ra ta có: Cứ lên cao 100m thì nhiệt độ không khí giảm khoảng 0,6^oC

Tại độ cao 2800m, nhiệt độ không khí giảm là: \(\frac{{2800}}{{100}}.0,6 = 16,{8^0}C\)

=> Nhiệt độ không khí bên ngoài là: 28 – 16,8 = 11,2⁰C

b) Đổi \(\frac{{22}}{5}km = \frac{{22000}}{5}m = 4400m\)

Ta có: Cứ lên cao 100m thì nhiệt độ không khí giảm khoảng 0,6^oC

Tại độ cao 4400m, nhiệt độ không khí giảm: \(\frac{{4400}}{{100}}.0,6 = 26,{4^0}C\)

=> Nhiệt độ trên mặt đất tại vùng trời khinh khí cầu đang bay lúc đó là -8,5 + 26,4 = 17,9 ^oC

Vậy nhiệt độ trên mặt đất tại vùng trời khinh khí cầu đang bay lúc đó là 17,9 ^oC

Bài 12 trang 16 Toán 7 tập 1

Em hãy tìm cách “nối” các ô vuông ở những cánh hoa bằng các dấu phép tính cộng, trừ, nhân, chia và dấu ngoặc để được một biểu thức có giá trị đúng bằng số ở nhị hoa.

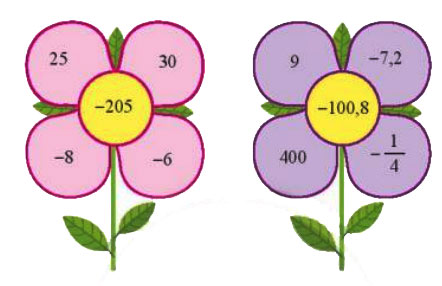
Gợi ý đáp án:

Ta có:

25 . (-8) + 30 : (-6) = -205

\(- \frac{1}{4}.400 + \left( { - 7,2} \right):9 = - 100,8\)