Toán 7 Bài tập cuối chương 8 - Chân trời sáng tạo Giải Toán lớp 7 trang 84 - Tập 2

Giải Toán 7 Bài tập cuối chương 8 giúp các em học sinh lớp 7 tham khảo phương pháp giải, hướng dẫn giải chi tiết các bài tập trong SGK Toán 7 Tập 2 sách Chân trời sáng tạo trang 84.

Qua đó, các em sẽ biết cách giải các bài toán góc và cạnh của một tam giác, tam giác bằng nhau, tam giác cân, đường vuông vóc, đường xiên.... Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài tập cuối chương 8: Tam giác trong SGK Toán 7 Tập 2 Chân trời sáng tạo. Chi tiết mời thầy cô và các em cùng theo dõi:

Giải Toán 7 Chân trời sáng tạo trang 84 tập 2

Bài 1

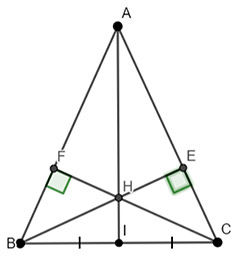
Cho tam giác ABC cân tại \(A (\widehat{A} < 90°)\). Hai đường cao BE và CF cắt nhau tại H.

a) Chứng minh rằng ∆BEC = ∆CFB.

b) Chứng minh rằng ∆AHF = ∆AHE.

c) Gọi I là trung điểm của BC. Chứng minh rằng ba điểm A, H, I thẳng hàng.

Phương pháp giải:

a) Ta sử dụng định lí cạnh huyền – góc nhọn trong tam giác vuông

b) Từ câu a ta chứng minh 2 tam giác AHF = tam giác AHE nhờ những cạnh của 2 tam giác chứng minh được bằng nhau từ câu trên

c) Ta chứng minh AI và AH cùng là phân giác của góc A

Gợi ý đáp án:

a) ∆ ABC cân tại \(A => \widehat{ABC} = \widehat{ACB}\) và AB = AC

\(=> \widehat{FBC} = \widehat{ECB}\)

BE và CF là hai đường cao của ∆ ABC

=> ∆BEC và ∆CFB là 2 tam giác vuông lần lượt tại E và F.

+ Xét ∆BEC vuông tại E và ∆CFB vuông tại F có:

BC chung

\(\widehat{FBC} = \widehat{ECB}\)

=> ∆BEC = ∆CFB (góc nhọn và một cạnh góc vuông)

b) Theo a: ∆BEC =∆CFB

=> EC = FB

Có AF = AB - FB

AE= AC - EC

Mà AB = AC, EC = FB

=> AF = AE

BE và CF là hai đường cao cắt nhau tại H

=> ∆AFH và ∆AEH là 2 tam giác vuông lần lượt tại F và E.

+ Xét ∆AFH vuông tại F và ∆AEH vuông tại E có:

AH chung

AF = AE

=> ∆AFH = ∆AEH (cạnh huyền và một cạnh góc vuông).

c) H là giao điểm của 2 đường cao BE và CF trong tam giác ABC

=> H là trực tâm của ∆ABC

=> AH ⊥ BC (1)

Có I là trung điểm của BC

=> AI là đường trung tuyến của ∆ ABC

Xét ∆ABI và ∆ACI có:

AB = AC

AI chung

IB = IC (I là trung điểm của BC)

=> ∆ABI = ∆ACI (c.c.c)

\(=> \widehat{AIC} = \widehat{AIB}\)

Có \(\widehat{AIC} + \widehat{AIB} = 180°\)

\(=> 2\widehat{AIB} = 180°\)

\(=> \widehat{AIB} = 90°\)

=> AI ⊥ BC (2)

Từ (1) và (2) => A, I, H thẳng hàng.

Bài 2

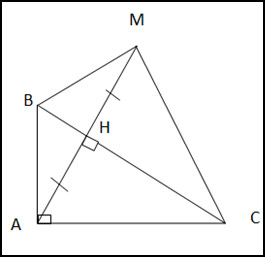
Cho tam giác ABC vuông tại A, vẽ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.

a) Chứng minh tam giác ABM cân.

b) Chứng minh rằng ∆ABC = ∆MBC.

Phương pháp giải:

a) Ta chứng minh BM = BA thông qua việc chứng minh 2 tam giác BHA và BHM bằng nhau

b) Ta chứng minh góc ABH = góc MBH sau đó chứng minh 2 tam giác đề bài yêu cầu bằng nhau theo trường hợp c-g-c

Gợi ý đáp án:

a) Có AH là đường cao của ∆ABC

=> AH ⊥ BC hay AM ⊥ BH

=> ∆BHA và ∆AHM là 2 tam giác vuông tại H

Xét ∆BHA và ∆BHM cùng vuông tại H có:

BH chung

AH = HM

=> ∆BHA = ∆BHM (hai cạnh góc vuông)

=> BA = BM

=> ∆ABM cân tại B.

b) Theo a: ∆BHA = ∆BHM

\(=> \widehat{ABH} = \widehat{MBH}\) hay \(\widehat{ABC} = \widehat{MBC}\)

Xét ∆ABC và ∆MBC có:

BC chung

\(\widehat{ABC} = \widehat{MBC}\)

AB = BM

=> ∆ABC = ∆MBC (c.g.c)

Bài 3

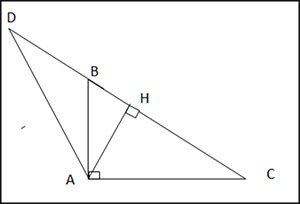
Cho tam giác ABC vuông tại A (AB, AC), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho HD = DC.

a) Chứng minh AC = AD.

b) Chứng minh rằng \(\widehat{ADB} = \widehat{BAH}\)

Gợi ý đáp án:

a) Ta có AH là đường cao của ∆ABC

=> ∆AHD và ∆AHC là 2 tam giác vuông tại H

Xét ∆AHD và ∆AHC cùng vuông tại H có:

AH chung

HD = HC

=> ∆AHD và ∆AHC (hai cạnh góc vuông)

=> AC = AD

b) + ∆ABC vuông tại A nên \(\widehat{ABC} + \widehat{ACB}= 90°\)

∆ABH vuông tại H nên \(\widehat{ABH} + \widehat{HAB}= 90°\)

\(=> \widehat{ACB} = \widehat{HAB}\)

+ Có AC = AD => ∆ ACD cân tại A

\(=> \widehat{ACD} = \widehat{ADC}\)

Mà \(\widehat{ACB} = \widehat{HAB}\)

\(=> \widehat{ADB} = \widehat{HAB}\).

Bài 4

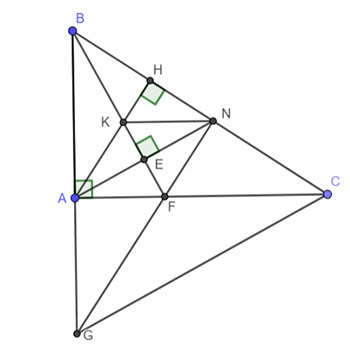
Cho tam giác vuông ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ BE ⊥ AN (E thuộc AN).

a) Chứng minh rằng BE là tia phân giác của góc ABN.

b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của AH với BE. Chứng minh rằng NK // CA.

c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB và NF. Chứng minh rằng tam giác GBC cân.

Gợi ý đáp án:

a) Xét ∆ABE và ∆NBE cùng vuông tại E có:

AB = BN

BE chung

=> ∆ABE = ∆NBE (cạnh huyền và một cạnh góc vuông).

\(=> \widehat{ABE} = \widehat{NBE}\)

=> BE là tia phân giác của góc ABN.

b) Xét tam giác ABN có: AH và BE là hai đường cao cắt nhau tại K

=> K là trực tâm tam giác ABN

=> NK ⊥ AB

mà AC ⊥ AB

=> NK // AC.

c) Xét ∆FBN và ∆ FBA có:

BN = BA

\(\widehat{NBF} = \widehat{ABF}\) (chứng minh trên)

BF chung

=> ∆FBN và ∆FBA (c.g.c)

mà ∆ FBA vuông tại A

=> ∆ FBN vuông tại N

=> BN ⊥ FN hay BN ⊥ GN

=> ∆ BNG vuông tại N

Xét 2 tam giác vuông ∆BNG và ∆BAC có

BN = BA

\(\widehat{ABN}\) chung

=> ∆BNG = ∆BAC (góc nhọn và một cạnh góc vuông)

=> BG = BC

=> ∆ BCG cân tại B.

Bài 5

Cho tam giác ABC nhọn (AB < AC), vẽ đường cao AH. Đường trung trực của cạnh BC cắt AC tại M, cắt BC tại N.

a) Chứng minh rằng \(\widehat{BMN} = \widehat{HAC}\).

b) Kẻ MI ⊥ AH (I thuộc AH), gọi K là giao điểm của AH với BM. Chứng minh rằng I là trung điểm của AK.

Gợi ý đáp án:

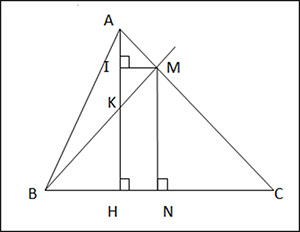
a) M, N thuộc đường trung trực của BC

=> MB = MC, NB = NC

=> ∆ MBC cân tại M, N là trung điểm của BC

=> MN là đường trung tuyến của ∆ MBC cân tại M

Xét ∆ MBN và ∆ MCN có:

MB = MC

BN = NC

MN chung

=> ∆ MBN = ∆ MCN (c.c.c)

\(=> \widehat{BMN} = \widehat{CMN}\)

∆ AHC vuông góc tại H

\(=> \widehat{HAC} + \widehat{HCA} = 90°\)

Hay \(\widehat{MCN} + \widehat{HAC} = 90° (1)\)

∆ MNC vuông góc tại N (MN là đường trung trực của BC)

\(=> \widehat{MCN} + \widehat{NMC} = 90°\)

Mà \(\widehat{BMN} = \widehat{CMN}\)

\(=> \widehat{MCN} +\widehat{HAC} = 90° (2)\)

Từ (1) và (2) ta có: \(\widehat{HAC} = \widehat{BMN}\)

b) Kẻ MI ⊥ AH

AH ⊥ BC

=> IM // BC

\(=> \widehat{IMB} = \widehat{MBC}\)(góc so le trong)

\(\widehat{AMI} = \widehat{MCB}\) (2 góc đồng vị)

Mà ∆MBC cân tại M nên \(\widehat{MBC} = \widehat{MBC}\)

\(=> \widehat{IMB} = \widehat{AMI}\)

Xét ∆MIK và ∆MIA cùng vuông tại I có:

MI chung

\(\widehat{IMK} = \widehat{AMI}\)(chứng minh trên)

=> ∆MIK = ∆MIA (góc nhọn và một cạnh góc vuông).

=> IK = IA

=> I là trung điểm của AK.

Bài 6

Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FN = FD.

a) Chứng minh rằng ∆ MFN = ∆ PFD.

b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm của HG. Gọi K là trung điểm của PD. Chứng minh rằng 3 điểm M, H, K thẳng hàng.

Gợi ý đáp án:

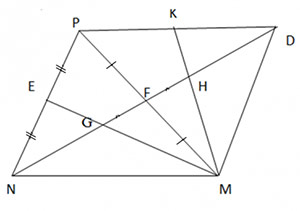
a) ME, NF là trung tuyến của ∆MNP

=> E là trung điểm của PN, F là trung điểm của PM

Xét ∆ MFN và ∆ PFD có

FN = FD

\(\widehat{MFN} = \widehat{PFD}\) (2 góc đối đỉnh)

FM = FP (F là trung điểm của PM)

=> ∆MFN = ∆PFD (c.g.c).

b)

+ Trong ∆MNP các trung tuyến ME và NF cắt nhau tại G.

=> G là trọng tâm của ∆MNP

\(=> FG = \frac{1}{3} FN\)

Mà FG = FH (F là trung điểm của HG); FN = FD

\(=> FH = \frac{1}{3} FD => DH = \frac{2}{3} FD\)

+ Xét tam giác PDM có: \(DH = \frac{2}{3} FD\)

Mà FD là đường trung tuyến của ∆PDM

=> H là trọng tâm của ∆PDM

=> MH là đường trung tuyến của ∆PDM (1)

K là trung điểm của PD

=> MK là đường trung tuyến của ∆PDM (2)

Từ (1) và (2)

=> M, H, K thẳng hàng.

Bài 7

Cho tam giác ABC vuông tại A có \(AB = \frac{1}{2} AC, AD\) là tia phân giác của \(\widehat{BAC}\) (D thuộc BC). Gọi E là trung điểm của AC.

a) Chứng minh rằng DE = DB.

b) AB cắt DE tại K. Chứng minh rằng tam giác DCK cân và B là trung điểm của đoạn thẳng AK.

c) AD cắt CK tại H. Chứng minh rằng AH ⊥ CK.

Gợi ý đáp án:

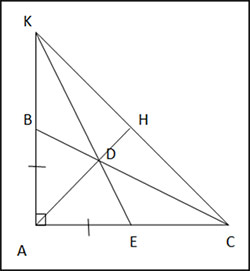
a) Xét ∆ABD và ∆AED có

AD chung

\(\widehat{BAD} = \widehat{EAD}\) (AD là đường phân giác)

AB = AE

=> ∆ ABD = ∆ AED (c.g.c)

=> BD = ED

b) + Chứng minh tam giác DCK cân.

Theo a: ∆ ABD = ∆ AED nên \(\widehat{DBA} = \widehat{DEA}\)

Ta có:

\(\widehat{DBK} + \widehat{DBA} = 180°\)

\(\widehat{DEC} + \widehat{DEA} = 180°\)

Mà \(\widehat{DBA} = \widehat{DEA}\)

\(=> \widehat{DBK} = \widehat{DEC}\)

Xét ∆CDE và ∆KDB có:

\(\widehat{KDB} = \widehat{CDE}\) (2 góc đối đỉnh)

DE = DB (chứng minh câu a)

\(\widehat{DBK} = \widehat{DEC}\) (chứng minh trên)

=> ∆CDE = ∆KDB (g.c.g)

=> DC = DK

=> ∆DCK cân tại D

+ Chứng minh B là trung điểm của đoạn thẳng AK.

Ta có: ∆CDE = ∆KDB nên EC = KB

Mà E là trung điểm của AC nên \(EC = AE = \frac{1}{2} AC\)

Mà \(AB = \frac{1}{2} AC\)

=> KB = AB

Mà A, B, K thẳng hàng

=> B là trung điểm của AK

c) B là trung điểm của AK

\(=>AB = \frac{1}{2} AK\)

Mà \(AB = \frac{1}{2} AC\)

=> AK = AC

Xét ∆KAH và ∆CAH có:

AK = AC

\(\widehat{KAH} = \widehat{CAH}\) (AD là đường phân giác của \(\widehat{BAC}\))

AH chung

=> ∆KAH = ∆CAH (c.g.c)

\(=> \widehat{AHK} = \widehat{AHC}\)

Mà \(\widehat{AHK} + \widehat{AHC} = 180°\)

\(=> 2\widehat{AHC} = 180°\)

\(=> \widehat{AHC} = 90°\)

=> AH ⊥ HC hay AH ⊥ CK.

Bài 8

Ở hình 1, cho biết AE = AF và \(\widehat{ABC} = \widehat{ACB}\). Chứng minh rằng AH là đường trung trực của BC

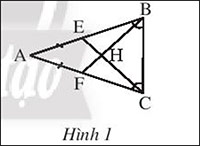
Gợi ý đáp án:

\(\widehat{ABC} = \widehat{ACB}\)

=> ∆ ABC cân tại A

=> AB = AC

=> A thuộc đường trung trực của BC (1)

Ta có: FC = AC - AF

EB = AB - AE

Mà AB = AC, AE= AF

=> FC = CB

Xét ∆ FCB và ∆ EBC có:

BC chung

\(\widehat{FCB} = \widehat{EBC}\)

FC = CB (chứng minh trên)

=> ∆FCB = ∆EBC (c.g.c)

\(=> \widehat{FBC} = \widehat{ECB}\)

=> ∆HCB cân tại H

=> HC = HB

=> H thuộc đường trung trực của BC (2)

Từ (1) và (2) => AH là đường trung trực của BC.

Bài 9

Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB tại M. Từ B kẻ BH vuông góc với đường thẳng CM (H thuộc CM). Trên tia đối của HC lấy điểm E sao cho HE = HM.

a) Chứng minh rằng tam giác MBE cân.

b) Chứng minh rằng \(\widehat{EBH}= \widehat{ACM}\)

c) Chứng minh rằng EB ⊥ BC.

Bài 10

Trên đường thẳng a lấy 3 điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.