Toán 10: Bài tập cuối chương IV - Cánh diều Giải SGK Toán 10 trang 99 - Tập 1

Giải Toán 10 Bài tập cuối chương IV  giúp các em học sinh lớp 10 tham khảo, biết cách giải các bài tập trong SGK Toán 10 Tập 1 trang 99, 100 sách Cánh diều.

Giải SGK Toán 10 Bài tập cuối chương 4: Hệ thức lượng trong tam giác vectơ sách Cánh diều Tập 1 giúp các em học sinh nắm được cách trình bày, cách triển khai để giải được các bài tập từ bài 1 đến bài 9 trong sách giáo khoa. Từ đó các em học sinh tự bồi dưỡng và nâng cao kiến thức tự tin giải quyết tốt các bài tập. Đồng thời đây cũng là tư liệu hữu ích giúp thầy cô tham khảo để soạn giáo án cho riêng mình.

Giải SGK Toán 10 trang 99, 100 - Tập 1

Bài 1 trang 99

Cho tam giác ABC có A B=3, A C=4, \(\widehat{B A C}=120^{\circ}\). Tính (làm tròn kết quả đến hàng đơn vị):

a. Độ dài cạnh BC và độ lớn góc B

b. Bán kính đường tròn ngoại tiếp

c. Diện tích của tam giác

d. Độ dài đường cao xuất phát từ A

e.\(\overrightarrow{A B} \cdot \overrightarrow{A C}, \overrightarrow{A M} \cdot \overrightarrow{B C}\) với M là trung điểm của B C

Gợi ý đáp án

a.

Áp dụng định lý cosin:

\(BC^2=AB^2+AC^2-2AB.AC.cosA=37\)

\(\Rightarrow BC=\sqrt{37}\)

Áp dụng định lý sin:

\(\frac{BC}{sin A}=\frac{AC}{sin B} \Rightarrow \widehat{B}=34,7^{\circ}\)

\(b. \frac{BC}{sin A}=2R \Rightarrow R=\frac{\sqrt{37}}{\sqrt{3}}\)

\(c. S=\frac{1}{2}.AB.AC.sinA=3\sqrt{3}\)

\(d. S=\frac{1}{2}.AH.BC \Rightarrow AH = \frac{6\sqrt{3}}{\sqrt{37}}\) (H là chân đường cao)

\(e. \overrightarrow{A B} \cdot \overrightarrow{A C}=3 \cdot 4 \cdot cos120=-6\)

Bài 2 trang 99

Không dùng máy tính cầm tay, hãy tính giá trị của các biểu thức sau:

\(A=\left(\sin 20^{\circ}+\sin 70^{\circ}\right)^{2}+\left(\cos 20^{\circ}+\cos 110^{\circ}\right)^{2},\)

\(B=\tan 20^{\circ}+\cot 20^{\circ}+\tan 110^{\circ}+\cot 110^{\circ} .\)

Gợi ý đáp án

\(A=(\sin 20^{\circ}+\sin 70^{\circ})^{2}+(\cos 20^{\circ}+\cos 110^{\circ})^{2}\)

\(=(\cos 70^{\circ}+\cos 20^{\circ})^{2}+(\cos 20^{\circ}+\cos 110^{\circ})^{2}\)

\(=(-\cos 110^{\circ}+\cos 20^{\circ})^{2}+(\cos 20^{\circ}+\cos 110^{\circ})^{2}\)

\(=2((cos 20^{\circ})^{2}+(cos 110^{\circ})^{2})\)

\(=2((sin 70^{\circ})^{2}+(-cos 70^{\circ})^{2}) =2\)

\(B=\tan 20^{\circ}+\cot 20^{\circ}+\tan 110^{\circ}+\cot 110^{\circ}\)

\(=\cot 70^{\circ}+\tan 70^{\circ}-\tan 70^{\circ}-\cot 70^{\circ} =0\)

Bài 3 trang 99

Không dùng thước đo góc, làm thế nào để biết số đo góc đó.

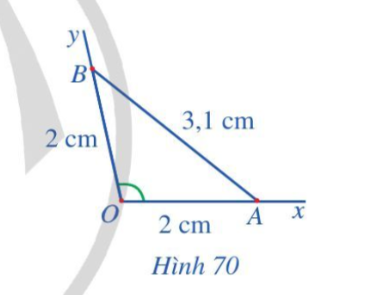
Bạn Hoài vẽ góc xOy và đố bạn Đông làm thế nào có thể biết được số đo của góc này khi không có thước đo góc. Bạn Đông làm như sau (Hình 70):

- Chọn các điểm A, B lần lượt thuộc các tia O x và O y sao cho O A=O B=2 cm

- Đo độ dài đoạn thẳng A B được \(A B=3,1 \mathrm{~cm}.\)

Từ các dữ kiện trên bạn Đông tính được \(cos\widehat{x O y}\), từ đó suy ra độ lớn góc x O y.

Em hãy cho biết số đo góc xOy mà bạn Đông tính được bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)

Gợi ý đáp án

\(cos\widehat{x O y}=\frac{OA^2+OB^2-AB^2}{2.OA.OB}=\frac{-161}{800}\)

\(\Rightarrow \widehat{x O y} \approx 101,6^{\circ}\)

Bài 4 trang 99

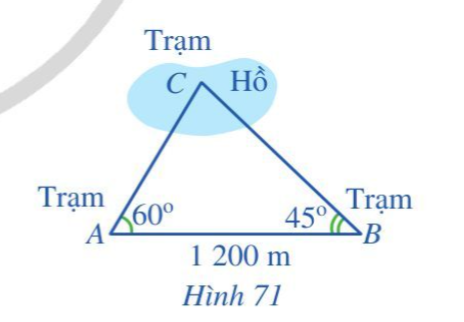
Có hai trạm quan sát A và B ven hồ và một trạm quan sát C ở giữa hồ. Để tính khoảng cách từ A và từ B đến C, người ta làm như sau (Hình 71):

Đo góc B A C được \(60^{\circ}\), đo góc A B C được \(45^{\circ};\)

Đo khoảng cách A B được 1200 m

Khoảng cách từ trạm C đến các trạm A và B bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Gợi ý đáp án

Ta có: \(\widehat{C}=180^{\circ}-\widehat{A}-\widehat{B}=75^{\circ}\)

Áp dụng định lý sin:\(\frac{BC}{sinA}=\frac{AC}{sinB}=\frac{AB}{sinC}\)

\(\Rightarrow \frac{BC}{sin60^{\circ}}=\frac{AC}{sin45^{\circ}}=\frac{1200}{sin75^{\circ}}\)

Vậy \(AC \approx 878,5\) (m) và \(BC \approx 1075,9\) (m)

Bài 5 trang 99

Một người đứng ở bờ sông, muốn đo độ rộng của khúc sông chảy qua vị trí đang đứng (khúc sông tương đối thẳng, có thể xem hai bờ song song với nhau).

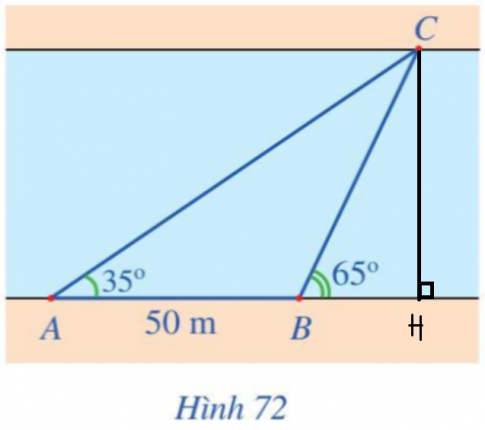
Từ vị trí đang đứng A, người đó đo được góc nghiêng \(\alpha=35^{\circ}\) so với bờ sông tới một vị trí C quan sát được ở phía bờ bên kia. Sau đó di chuyển dọc bờ sông đến vị trí B cách A một khoảng d=50 m và tiếp tục đo được góc nghiêng \(\beta=65^{\circ}\) so với bờ bên kia tới vị trí C đã chọn (Hình 72). Hỏi độ rộng của khúc sông chảy qua vị trí người đó đang đứng là bao nhiêu mét (làm trờn kết quả đến hàng phần mười)?

Gợi ý đáp án

Ta có: \(\widehat{ACB}=\widehat{CBH}-\widehat{CAB}=30^{\circ}\)

\(\widehat{HCB}=90^{\circ}-\widehat{CBH}=25^{\circ}\)

Áp dụng định lý sin:

\(CB=sin35^{\circ} \cdot \frac{AB}{^{sin30^\circ}} \approx 57,4\)

\(CH= sin65^{\circ} \cdot \frac{CB}{^{sin90^\circ}} \approx 52\)

Vì hai bờ sông song song nên độ rộng của khúc sông chảy qua vị trí người đó đang đứng là 52 m.

Bài 6 trang 100

Để đo khoảng cách giữa hai vị trí M, N ở hai phía ốc đảo, người ta chọn vị trí O bên ngoài ốc đảo sao cho: O không thuộc đường thẳng M N; các khoảng cách O M, ON và góc MON là đo đước (Hình 73 ). Sau khi đo, ta có\(O M=200 \mathrm{~m}, O N=500 \mathrm{~m}, \widehat{M O N}=135^{\circ}.\)

Khoảng cách giữa hai vị trí M, N là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Gợi ý đáp án

Áp dụng định lí côsin: \(MN^2=OM^2+ON^2-2.OM.OM.cos35^{\circ}\)

\(MN=\sqrt{OM^2+ON^2-2.OM.OM.cos35^{\circ}}\approx 656,8 (m)\)

Bài 7 trang 100

Chứng minh:

a. Nếu A B C D là hình bình hành thì \(\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{C E}=\overrightarrow{A E}\) vơi E là điểm bất kì;

b. Nếu I là trung điểm của đoạn thẳng A B thì \(\overrightarrow{M A}+\overrightarrow{M B}+2 \overrightarrow{I N}=2 \overrightarrow{M N}\) với M, N là hai điểm bất kì;

c. Nếu G là trọng tâm của tam giác A B C thì \(\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}-3 \overrightarrow{M N}=3 \overrightarrow{N G}\) với M, N là hai điểm bất kì.

Gợi ý đáp án

a. Áp dụng quy tắc hình bình hành:\(\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{C E}=\overrightarrow{AC}+\overrightarrow{C E}=\overrightarrow{A E}\) (đpcm)

b.\(\overrightarrow{M A}+\overrightarrow{M B}+2 \overrightarrow{I N}=\overrightarrow{M A}+\overrightarrow{I N}+\overrightarrow{M B}+\overrightarrow{I N}\)

\(=\overrightarrow{M A}+\overrightarrow{IM}+\overrightarrow{MN}+\overrightarrow{M B}+\overrightarrow{IM}+\overrightarrow{MN}\)

=\(2 \overrightarrow{M N}+\overrightarrow{IA}+\overrightarrow{IB}\)

\(=2 \overrightarrow{M N}\) (đpcm)

c.\(\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}-3 \overrightarrow{M N}\)

\(=3\overrightarrow{MG}+\overrightarrow{G A}+\overrightarrow{GB}+\overrightarrow{G C}-3 \overrightarrow{MG}+\overrightarrow{N G}\)

\(=3 \overrightarrow{N G}\)(do G là trọng tâm của tam giác A B C) (đpcm)

Bài 8 trang 100

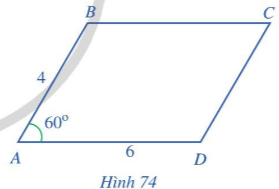
Cho hình bình hành A B C D có A B=4, A D=6, \(\widehat{B A D}=60^{\circ}\) (Hình 74).

a. Biểu thị các vectơ \(\overrightarrow{B D}, \overrightarrow{A C}\) theo \(\overrightarrow{A B}, \overrightarrow{A D}.\)

b. Tính các tích vô hướng \(\overrightarrow{A B} \cdot \overrightarrow{A D}, \overrightarrow{A B} \cdot \overrightarrow{A C}, \overrightarrow{BD} \cdot \overrightarrow{A C}\)

c. Tính độ dài các đường chéo B D, A C.

Gợi ý đáp án

a. Áp dụng quy tắc hình bình hành:

\(\overrightarrow{B D}=\overrightarrow{BA}+\overrightarrow{BC}=-\overrightarrow{AB}+\overrightarrow{AD}\)

\(\overrightarrow{A C}=\overrightarrow{AB}+\overrightarrow{AD}\)

b.

\(\overrightarrow{A B} \cdot \overrightarrow{A D}=4 \cdot 6 \cdot cos60^{\circ}=12\)

\(\overrightarrow{A B} \cdot \overrightarrow{A C}=\overrightarrow{A B} \cdot (\overrightarrow{AD}+\overrightarrow{DC})=\overrightarrow{A B} \cdot \overrightarrow{A D}+(\overrightarrow{A B})^2=12+16=28\)

\(\overrightarrow{BD} \cdot \overrightarrow{A C}=(\overrightarrow{BC} +\overrightarrow{CD})(\overrightarrow{AD}+\overrightarrow{DC})=(\overrightarrow{AD} -\overrightarrow{AB})(\overrightarrow{AD}+\overrightarrow{AB})=(\overrightarrow{AD})^2+(\overrightarrow{AB})^2\)

\(=4^2+6^2=52\)

c. Áp dụng định lí côsin:

\(AC=\sqrt{AB^2+BC^2-2.AB.BC.cos120^{\circ}}=\sqrt{76}\)

\(BD=\sqrt{AB^2+AD^2-2.AB.AD.cos60^{\circ}}=\sqrt{28}\)

Bài 9 trang 100

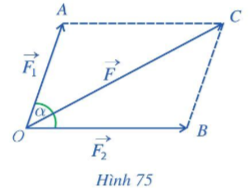
Hai lực \(\overrightarrow{F_{1}}, \overrightarrow{F_{2}}\) cho trước cùng tác dụng lên một vật tại điểm O và tạo với nhau một góc \(\left(\overrightarrow{F_{1}}, \overrightarrow{F_{2}}\right)=\alpha\) làm cho vật di chuyển theo hướng từ O đến C (Hình 75). Lập công thức tính cường độ của hợp lực \(\vec{F}\) làm cho vật di chuyển theo hướng từ O đến C (giả sử chỉ có đúng hai lực \(\vec{F}_{1}, \overrightarrow{F_{2}}\) làm cho vật di chuyển).

Gợi ý đáp án

Áp dụng quy tắc hình bình hành: \(\vec{F}=\vec{F}_{1}+\vec{F}_{2}\)

Áp dụng định lý cosin:\(|\vec{F}|^2=|\vec{F}_{1}|^2+|\vec{F}_{2}|^2-2 \cdot |\vec{F}_{1}| \cdot |\vec{F}_{2}| \cdot cos (180^{\circ}-\alpha)\)

\(=|\vec{F}_{1}|^2+|\vec{F}_{2}|^2+2 \cdot |\vec{F}_{1}| \cdot |\vec{F}_{2}| \cdot cos \alpha\)

Cường độ của hợp lực \(\vec{F}\) là:\(\sqrt{{F}_{1}^2+{F}_{2}^2+2 \cdot {F}_{1} \cdot {F}_{2}\cdot cos \alpha}\)