Toán 10 Bài 1: Tọa độ của vectơ Giải SGK Toán 10 trang 62 - Tập 2 sách Cánh diều

Bài trước

Mục lục

Bài sau

Giải Toán 10 Bài 1: Tọa độ của vectơ sách Cánh diều là tài liệu vô cùng hữu ích giúp các em học sinh lớp 10 có thêm nhiều gợi ý tham khảo, dễ dàng đối chiếu kết quả khi làm bài tập toán trang 62 tập 2.

Giải SGK Toán 10 Bài 1 trang 62 Cánh diều tập 2 được biên soạn chi tiết, bám sát nội dung trong sách giáo khoa. Mỗi bài toán đều được giải thích cụ thể, chi tiết. Qua đó giúp các em củng cố, khắc sâu thêm kiến thức đã học trong chương trình chính khóa. Nội dung chi tiết bài Giải Toán 10 Bài 1 chương 7 trang 62 tập 2 mời các bạn cùng đón đọc tại đây.

Toán 10 Bài 1: Tọa độ của vectơ

Giải Toán 10 trang 62 Cánh diều - Tập 2

Giải Toán 10 trang 62 Cánh diều - Tập 2

Bài 1

Tìm tọa độ của các vecto trong Hình 16 và biểu diễn mỗi vecto đó qua hai vecto $\vec{i} ,\vec{j}$ $\vec{i} ,\vec{j}$

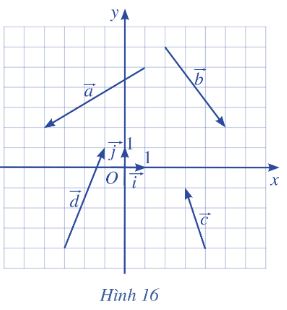
Gợi ý đáp án

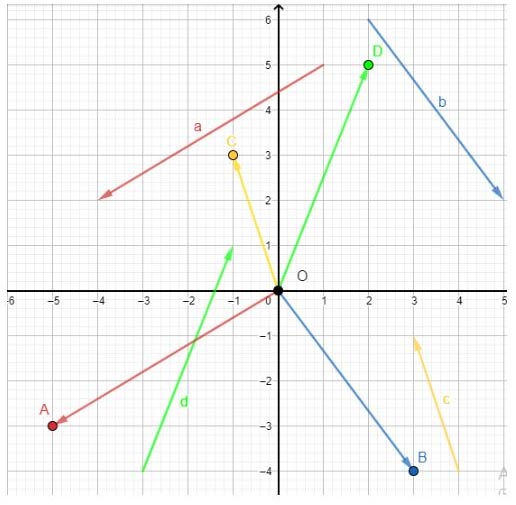
Dựa vào hình vẽ, ta thấy tọa độ của 4 điểm A, B, C, D là:

$\begin{aligned} & A(-5 ;-3), B(3 ;-4), C(-1 ; 3), D(2 ; 5) \\ & \text { Do đó } \\ & \vec{a}=\overrightarrow{O A}=(-5 ;-3), \vec{b}=\overrightarrow{O B}=(3 ;-4), \vec{c}=\overrightarrow{O C}=(-1 ; 3), \vec{d} \\ & =\overrightarrow{O D}=(2 ; 5) \\ & \text { b) vi } \vec{a}=\overrightarrow{O A}=(-5 ;-3) \text { nên } \vec{a}=(-5) \vec{i}+(-3) \vec{j}=-5 \vec{i}-3 \vec{j} \\ & \text { vi } \vec{b}=\overrightarrow{O B}=(3 ;-4) \text { nên } \vec{b}=3 \vec{i}+(-4) \vec{j}=3 \vec{i}-4 \vec{j} \\ & \text { vi } \vec{c}=\overrightarrow{O C}=(-1 ; 3) \text { nên } \vec{c}=(-1) \vec{i}+(3) \vec{j}=-\vec{i}+3 \vec{j} \\ & \text { vi } \vec{d}=\overrightarrow{O D}=(2 ; 5) \text { nên } \vec{d}=2 \vec{i}+5 \vec{j} \end{aligned}$ $\begin{aligned} & A(-5 ;-3), B(3 ;-4), C(-1 ; 3), D(2 ; 5) \\ & \text { Do đó } \\ & \vec{a}=\overrightarrow{O A}=(-5 ;-3), \vec{b}=\overrightarrow{O B}=(3 ;-4), \vec{c}=\overrightarrow{O C}=(-1 ; 3), \vec{d} \\ & =\overrightarrow{O D}=(2 ; 5) \\ & \text { b) vi } \vec{a}=\overrightarrow{O A}=(-5 ;-3) \text { nên } \vec{a}=(-5) \vec{i}+(-3) \vec{j}=-5 \vec{i}-3 \vec{j} \\ & \text { vi } \vec{b}=\overrightarrow{O B}=(3 ;-4) \text { nên } \vec{b}=3 \vec{i}+(-4) \vec{j}=3 \vec{i}-4 \vec{j} \\ & \text { vi } \vec{c}=\overrightarrow{O C}=(-1 ; 3) \text { nên } \vec{c}=(-1) \vec{i}+(3) \vec{j}=-\vec{i}+3 \vec{j} \\ & \text { vi } \vec{d}=\overrightarrow{O D}=(2 ; 5) \text { nên } \vec{d}=2 \vec{i}+5 \vec{j} \end{aligned}$

Bài 2

Tìm tọa độ của các vecto sau:

$a) \vec{a}=3 \vec{i}$ $a) \vec{a}=3 \vec{i}$

$b) \vec{b}=-\vec{j}$ $b) \vec{b}=-\vec{j}$

$c) \vec{c}=\vec{i}-4 \vec{j}$ $c) \vec{c}=\vec{i}-4 \vec{j}$

$d) \vec{d}=0,5 \vec{i}+\sqrt{6} \vec{j}$ $d) \vec{d}=0,5 \vec{i}+\sqrt{6} \vec{j}$

Gợi ý đáp án

a) Vì $\vec{a}=3 \vec{i}$ $\vec{a}=3 \vec{i}$ nên $\vec{a}=(3 ; 0)$ $\vec{a}=(3 ; 0)$

b) Vì $\vec{b}=-\vec{j}$ $\vec{b}=-\vec{j}$ nên $\vec{b}=(0 ;-1)$ $\vec{b}=(0 ;-1)$

c) Vì $\vec{c}=\vec{i}-4 \vec{j}$ $\vec{c}=\vec{i}-4 \vec{j}$ nên $\vec{c}=(1 ;-4)$ $\vec{c}=(1 ;-4)$

d) Vì $\vec{d}=0,5 \vec{i}+\sqrt{6} \vec{j}$ $\vec{d}=0,5 \vec{i}+\sqrt{6} \vec{j}$ nên $\vec{d}=(0,5 ; \sqrt{6})$ $\vec{d}=(0,5 ; \sqrt{6})$

Bài 3

Tìm các cặp số thực a và b sao cho mỗi cặp vecto sau bằng nhau:

a) $\vec{u}=(2 a-1 ;-3)$ $\vec{u}=(2 a-1 ;-3)$ và $\vec{v}=(3 ; 4 b+1)$ $\vec{v}=(3 ; 4 b+1)$

b) $\vec{x}=(a+b ;-2 a+3 b)$ $\vec{x}=(a+b ;-2 a+3 b)$ và $\vec{y}=(2 a-3 ; 4 b)$ $\vec{y}=(2 a-3 ; 4 b)$

Gợi ý đáp án

a) Để $\vec{u}=\vec{v} \Leftrightarrow\left\{\begin{array}{l}2 a-1=3 \\ -3=4 b+1\end{array} \Leftrightarrow\left\{\begin{array}{l}a=2 \\ b=-1\end{array}\right.\right.$ $\vec{u}=\vec{v} \Leftrightarrow\left\{\begin{array}{l}2 a-1=3 \\ -3=4 b+1\end{array} \Leftrightarrow\left\{\begin{array}{l}a=2 \\ b=-1\end{array}\right.\right.$

Vậy $\left\{\begin{array}{l}a=2 \\ b=-1\end{array}\right.$ $\left\{\begin{array}{l}a=2 \\ b=-1\end{array}\right.$ thì $\vec{u}=\vec{v}$ $\vec{u}=\vec{v}$

b) $\vec{x}=\vec{y} \Leftrightarrow\left\{\begin{array}{l}a+b=2 a-3 \\ -2 a+3 b=4 b\end{array} \Leftrightarrow\left\{\begin{array}{l}a=1 \\ b=-2\end{array}\right.\right.$ $\vec{x}=\vec{y} \Leftrightarrow\left\{\begin{array}{l}a+b=2 a-3 \\ -2 a+3 b=4 b\end{array} \Leftrightarrow\left\{\begin{array}{l}a=1 \\ b=-2\end{array}\right.\right.$

Vậy $\left\{\begin{array}{l}a=1 \\ b=-2\end{array}\right. thì \vec{x}=\vec{y}$ $\left\{\begin{array}{l}a=1 \\ b=-2\end{array}\right. thì \vec{x}=\vec{y}$

Bài 4

Trong mặt phẳng toạ độ Oxy, cho ba điểm A(2;3), B(-1; 1), C(3;- 1).

a) Tìm toạ độ điểm M sao cho $\vec{AM} =\vec{BC}$ $\vec{AM} =\vec{BC}$.

b) Tìm toạ độ trung điểm N của đoạn thẳng AC. Chứng minh $\vec{BN} =\vec{NM}$ $\vec{BN} =\vec{NM}$.

Gợi ý đáp án

a) Gọi $M(a ; b) \Rightarrow \overrightarrow{A M}=(a-2 ; b-3)$ $M(a ; b) \Rightarrow \overrightarrow{A M}=(a-2 ; b-3)$

Tọa độ vecto $\overrightarrow{B C}=(4 ;-2)$ $\overrightarrow{B C}=(4 ;-2)$

Đề $\overrightarrow{A M}=\overrightarrow{B C} \Leftrightarrow\left\{\begin{array}{l}a-2=4 \\ b-3=-2\end{array} \Leftrightarrow\left\{\begin{array}{l}a=6 \\ b=1\end{array}\right.\right.$ $\overrightarrow{A M}=\overrightarrow{B C} \Leftrightarrow\left\{\begin{array}{l}a-2=4 \\ b-3=-2\end{array} \Leftrightarrow\left\{\begin{array}{l}a=6 \\ b=1\end{array}\right.\right.$

Vậy để $\overrightarrow{A M}=\overrightarrow{B C}$ $\overrightarrow{A M}=\overrightarrow{B C}$ thì tọa độ điểm M là: M(6 ; 1)

b) Gọi $N(x, y) \Rightarrow \overrightarrow{N C}=(3-x,-1-y) và \overrightarrow{A C}=(x-2, y-3)$ $N(x, y) \Rightarrow \overrightarrow{N C}=(3-x,-1-y) và \overrightarrow{A C}=(x-2, y-3)$

Do N là trung điểm AC nên

$\overrightarrow{A C}=\overrightarrow{N C} \Leftrightarrow\left\{\begin{array}{l}x-2=3-x \\ y-3=-1-y\end{array} \Leftrightarrow\left\{\begin{array}{l}x=\frac{5}{2} \\ y=1\end{array}\right.\right.. Vậy N\left(\frac{5}{2}, 1\right)$ $\overrightarrow{A C}=\overrightarrow{N C} \Leftrightarrow\left\{\begin{array}{l}x-2=3-x \\ y-3=-1-y\end{array} \Leftrightarrow\left\{\begin{array}{l}x=\frac{5}{2} \\ y=1\end{array}\right.\right.. Vậy N\left(\frac{5}{2}, 1\right)$

Ta có: $\overrightarrow{B N}=\left(-\frac{7}{2} ; 0\right)$ $\overrightarrow{B N}=\left(-\frac{7}{2} ; 0\right)$ và $\overrightarrow{N M}=\left(\frac{-7}{2} ; 0\right)$ $\overrightarrow{N M}=\left(\frac{-7}{2} ; 0\right)$. vậy $\overrightarrow{B N}=\overrightarrow{N M}$ $\overrightarrow{B N}=\overrightarrow{N M}$

Bài 5

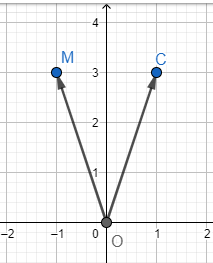
Trong mặt phẳng toạ độ Oxy, cho điểm M(-1; 3).

a) Tìm toạ độ điểm A đối xứng với điểm M qua gốc O.

b) Tìm toạ độ điểm B đối xứng với điểm M qua trục Ox.

c) Tìm toạ độ điểm C đối xứng với điểm M qua trục Oy.

Gợi ý đáp án

a) Dựa vào hình vẽ ta thấy A(1; −3)

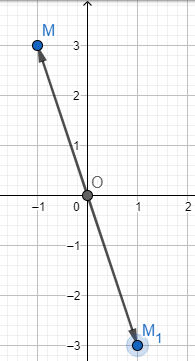
b) Dựa vào hình vẽ ta thấy B(−1; −3)

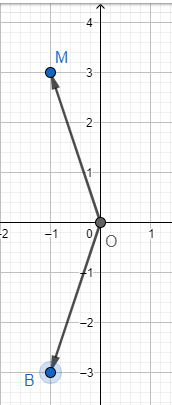
c) Dựa vào hình vẽ ta thấy C(1; 3)

Bài 6

Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(- 3 ; 1), B(-1; 3), I(4;2). Tìm toạ độ của hai điểm C, D sao cho tứ giác ABCD là hình bình hành nhận I làm tâm đối xứng.

Gợi ý đáp án

Gọi $C(a ; b), D(m, n) \Rightarrow \overrightarrow{I C}=(a-4, b-2) và \overrightarrow{I D}=(m-4, n-2)$ $C(a ; b), D(m, n) \Rightarrow \overrightarrow{I C}=(a-4, b-2) và \overrightarrow{I D}=(m-4, n-2)$

Do I là tâm của hình bình hành A B C D nên I là trung điểm A C và B D.

Vậy ta có: $\overrightarrow{A I}=\overrightarrow{I C} và \overrightarrow{B I}=\overrightarrow{I D}$ $\overrightarrow{A I}=\overrightarrow{I C} và \overrightarrow{B I}=\overrightarrow{I D}$

Ta có: $\overrightarrow{A I}=(7 ; 1)$ $\overrightarrow{A I}=(7 ; 1)$ và $\overrightarrow{B I}=(5 ;-1)$ $\overrightarrow{B I}=(5 ;-1)$

Do $\overrightarrow{A I}=\overrightarrow{I C} \Leftrightarrow\left\{\begin{array}{l}7=a-4 \\ 1=b-2\end{array} \Leftrightarrow\left\{\begin{array}{l}a=11 \\ b=3\end{array}\right.\right..$ $\overrightarrow{A I}=\overrightarrow{I C} \Leftrightarrow\left\{\begin{array}{l}7=a-4 \\ 1=b-2\end{array} \Leftrightarrow\left\{\begin{array}{l}a=11 \\ b=3\end{array}\right.\right..$

Vậy C(11 ; 3)

Do $\overrightarrow{B I}=\overrightarrow{I D} \Leftrightarrow\left\{\begin{array}{l}5=m-4 \\ -1=n-2\end{array} \Leftrightarrow\left\{\begin{array}{l}m=9 \\ n=1\end{array}\right.\right.$ $\overrightarrow{B I}=\overrightarrow{I D} \Leftrightarrow\left\{\begin{array}{l}5=m-4 \\ -1=n-2\end{array} \Leftrightarrow\left\{\begin{array}{l}m=9 \\ n=1\end{array}\right.\right.$.. Vậy D(9 ; 1)

Chia sẻ bởi: