Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn Giải SGK Toán 10 trang 24 - Tập 1 sách Cánh diều

Bài trước

Mục lục

Bài sau

Toán 10 Cánh diều trang 24 tập 1 giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi Khởi động, Hoạt động và 5 bài tập trong SGK bài Bất phương trình bậc nhất hai ẩn được chính xác thuận tiện hơn.

Giải Toán 10 Cánh diều trang 24 tập 1 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh lớp 10 học tốt môn Toán 10. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu Toán 10 trang 24 Cánh diều mời các bạn cùng theo dõi.

Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn

Phần Khởi động

Nhân dịp Tết Trung thu, một doanh nghiệp dự định sản xuất hai loại bánh: bánh nướng và bánh dẻo. Lượng đường cần cho mỗi chiếc bánh nướng, bánh dẻo lần lượt là 60 g, 50 g. Doanh nghiệp đã nhập về 500 kg đường.

Số bánh nướng và số bánh dẻo doanh nghiệp dự định sản xuất cần thỏa mãn điều kiện ràng buộc gì để lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về?

Gợi ý đáp án

Để tìm hiểu về câu hỏi này, chúng ta cùng theo dõi hoạt động 1 trang 20.

Phần Hoạt động

Hoạt động 1 trang 20 Toán 10 tập 1

Trong bài toán ở phần mở đầu, ta gọi $x,y$ lần lượt là số bánh nướng và số bánh dẻo doanh nghiệp dự định sản xuất ( $x,y$ là số tự nhiên). Nêu điều kiện ràng buộc đối với $x$ và $y$ để lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về.

Lời giải:

+ $x$ là số bánh nướng ⇒ Khối lượng đường cần cho số bánh nướng là: $60x$ g = kg.

+ $y$ là số bánh dẻo ⇒ Khối lượng đường cần cho số bánh dẻo là: $50y$ g = $0,05y$ kg.

+ Tổng số lượng đường cần dùng cho số bánh nướng và bánh dẻo là: $0,06x + 0,05y$ kg.

+ Để lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về, ta có ràng buộc sau:

$0,06x + 0,05y \leqslant 500$ $0,06x + 0,05y \leqslant 500$

Hoạt động 2 trang 21 Toán 10 tập 1

Trong mặt phẳng tọa độ $Oxy$, xác định các điểm $M\left( {x;y} \right)$ $M\left( {x;y} \right)$ mà:

a) $x > 0$ (1)

b) $y < 1$ (2)

Lời giải:

a) $x > 0$ (1)

+ Đường thẳng $x = 0$ mặt phẳng thành hai nửa: nửa mặt phẳng bên trái và nửa mặt phẳng bên phải trục tung.

+ Điểm $M\left( {x;y} \right)$ $M\left( {x;y} \right)$ trong mặt phẳng tọa độ thỏa mãn điều kiện $x > 0$ sẽ nằm ở nửa mặt phẳng bên phải trục tung.

Vậy miền nghiệm của bất phương trình (1) là nửa mặt phẳng bên phải trục tung, được mô tả bằng nửa mặt phẳng không được tô màu ở hình dưới đây: (Học sinh tự vẽ hình)

b. $y < 1$ (2)

+ Đường thẳng $y = 1$ mặt phẳng thành hai nửa: nửa mặt phẳng bên trên đường thẳng $y = 1$ và nửa mặt phẳng bên dưới đường thẳng $y = 1$.

+ Điểm $M\left( {x;y} \right)$ $M\left( {x;y} \right)$ trong mặt phẳng tọa độ thỏa mãn điều kiện $y < 1$ sẽ nằm ở nửa mặt phẳng bên dưới đường thẳng $y = 1$.

Vậy miền nghiệm của bất phương trình (1) là nửa mặt phẳng bên dưới đường thẳng $y = 1$, được mô tả bằng nửa mặt phẳng không được tô màu ở hình dưới đây: (Học sinh tự vẽ hình)

Giải Toán 10 trang 24 Cánh diều - Tập 1

Bài 1 trang 24 SGK Toán 10

Cặp số nào sau đây là nghiệm của bất phương trình 2x - 3y < 3?

$a) \left( {0; - 1} \right)$ $a) \left( {0; - 1} \right)$

$b) \left( {2;1} \right)$ $b) \left( {2;1} \right)$

$c) \left( {3;1} \right)$ $c) \left( {3;1} \right)$

Gợi ý đáp án

a) Thay x = 0,y = - 1vào bất phương trình 2x - 3y < 3 ta được:

$2.0 - 3.\left( { - 1} \right) < 3 \Leftrightarrow 3 < 3$ $2.0 - 3.\left( { - 1} \right) < 3 \Leftrightarrow 3 < 3$ (Vô lý)

Vậy $\left( {0; - 1} \right)$ $\left( {0; - 1} \right)$ không là nghiệm.

b) Thay x = 2, y = 1 vào bất phương trình 2x - 3y < 3 ta được:

2.2 - 3.1 < 3 $\Leftrightarrow$ $\Leftrightarrow$ 1 < 3 (Luôn đúng)

Vậy $\left( {2;1} \right)$ $\left( {2;1} \right)$ là nghiệm.

c) Thay x = 3,y = 1 vào bất phương trình 2x - 3y < 3 ta được:

2.3 - 3.1 < 3 $\Leftrightarrow$ $\Leftrightarrow$ 3 < 3 (Vô lý)

Vậy $\left( {3;1} \right)$ $\left( {3;1} \right)$ không là nghiệm.

Bài 2 trang 24 SGK Toán 10

Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) x + 2y < 3;

b) $3x - 4y \ge - 3;$ $3x - 4y \ge - 3;$

c) $y \ge - 2x + 4;$ $y \ge - 2x + 4;$

d) y < 1 - 2x.

Gợi ý đáp án

a) Ta vẽ đường thẳng d’: $x + 2y = 3 \Leftrightarrow y = - \frac{x}{2} + \frac{3}{2}$ $x + 2y = 3 \Leftrightarrow y = - \frac{x}{2} + \frac{3}{2}$

Thay tọa độ điểm O(0;0) vào bất phương trình x + 2y < 3 ta được:

0 + 2.0 = 0 < 3 (Luôn đúng)

Vậy O nằm trong miền nghiệm.

Ta có miền nghiệm:

b) Ta vẽ đường thẳng d: $3x - 4y = - 3 \Leftrightarrow y = \frac{{3x}}{4} + \frac{3}{4}$ $3x - 4y = - 3 \Leftrightarrow y = \frac{{3x}}{4} + \frac{3}{4}$

Thay tọa độ điểm O(0;0) vào bất phương trình $3x - 4y \ge - 3$ $3x - 4y \ge - 3$ ta được:

$3.0 - 4.0 = 0 \ge - 3$ $3.0 - 4.0 = 0 \ge - 3$ (Luôn đúng)

Vậy O nằm trong miền nghiệm.

Ta có miền nghiệm:

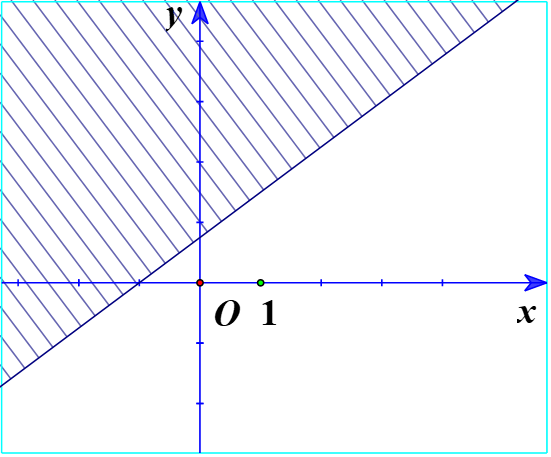
c) Ta vẽ đường thẳng d:y = - 2x + 4

Thay tọa độ điểm O(0;0) vào bất phương trình $y \ge - 2x + 4$ $y \ge - 2x + 4$ ta được:

$0 \ge - 2.0 + 4 \Leftrightarrow 0 \ge 4$ $0 \ge - 2.0 + 4 \Leftrightarrow 0 \ge 4$ (Vô lí)

Vậy O không nằm trong miền nghiệm.

Ta có miền nghiệm:

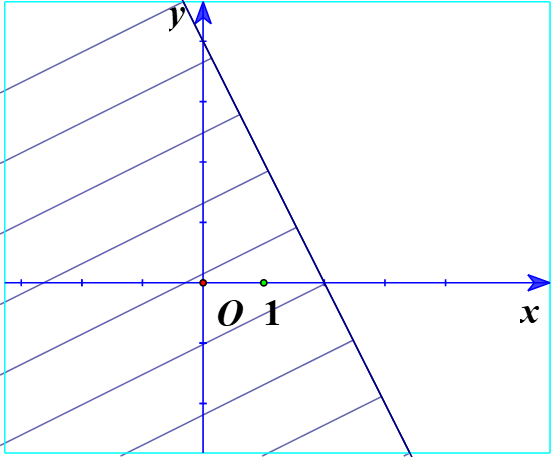
d) Ta vẽ đường thẳng d:y = 1 - 2x

Thay tọa độ điểm O(0;0) vào bất phương trình y < 1 - 2x ta được:

0 < 1 - 2.0 (Luôn đúng)

Vậy O nằm trong miền nghiệm.

Ta có miền nghiệm:

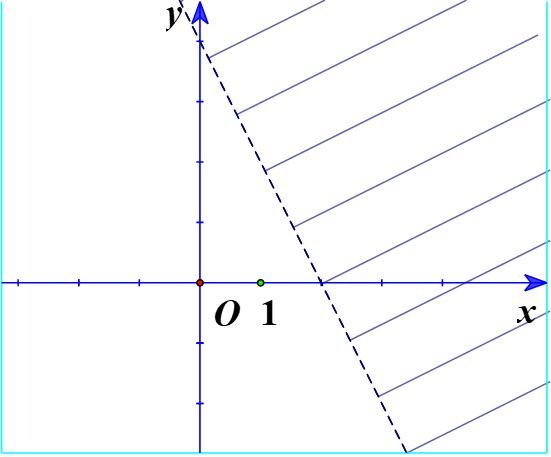
Bài 3 trang 24 SGK Toán 10

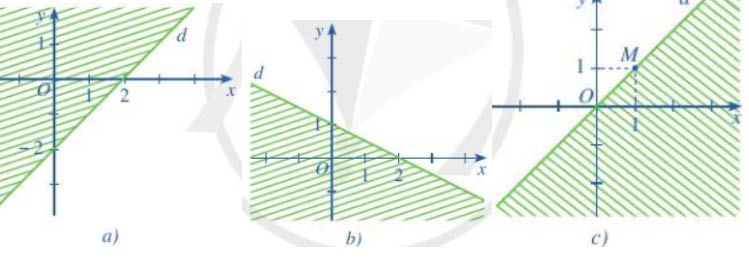
Phần không gạch (không kể d) ở mỗi Hình 7a, 7b, 7c là miền nghiệm của bất phương trình nào?

Gợi ý đáp án

a) Đường thẳng qua điểm (2;0) và (0;-2) nên phương trình đường thẳng là

x-y-2=0

Lấy điểm (3;0) thuộc miền nghiệm ta có 3-0-2=1>0

=> Bất phương trình cần tìm là $x - y - 2 \ge 0$ $x - y - 2 \ge 0$

b) Đường thẳng qua điểm (2;0) và (0;1) nên phương trình đường thẳng là

Thay x=2, y=0 vào phương trình y = ax + b ta được 0 = 2a + b

Thay x=0, y=1 vào phương trình y = ax + b ta được 1 = 0.a + b

$=> a = - \frac{1}{2},b = 1$ $=> a = - \frac{1}{2},b = 1$

=> phương trình đường thẳng là $y = - \frac{1}{2}x + 1$ $y = - \frac{1}{2}x + 1$

Lấy điểm (3;0) thuộc miền nghiệm ta có $- \frac{1}{2}x + 1 - y = \frac{{ - 1}}{2} < 0$ $- \frac{1}{2}x + 1 - y = \frac{{ - 1}}{2} < 0$

=> Bất phương trình cần tìm là $- \frac{1}{2}x - y + 1 \le 0$ $- \frac{1}{2}x - y + 1 \le 0$

c) Đường thẳng qua điểm (0;0) và (1;1) nên phương trình đường thẳng là

x-y=0

Lấy điểm (0;1) thuộc miền nghiệm ta có x-y=-1<0

=> Bất phương trình cần tìm là $x - y \le 0$ $x - y \le 0$

Bài 4 trang 24 SGK Toán 10

Một gian hàng trưng bày bàn và ghế rộng 60 ${m^2}$ ${m^2}$. Diện tích để kê một chiếc ghế là $0,5{m^2},$ $0,5{m^2},$ một chiếc bàn là $1,2 {m^2}$ $1,2 {m^2}$. Gọi x là số chiếc ghế, y là số chiếc bàn được kê.

a) Viết bất phương trình bậc nhất hai ẩn x, y cho phần mặt sàn để kê bàn và ghế, biết diện tích mặt sàn dành cho lưu thông tối thiểu là $12 {m^2}.$ $12 {m^2}.$

b) Chỉ ra ba nghiệm của bất phương trình trên.

Gợi ý đáp án

Bước 1: Biểu diễn diện tích x chiếc ghế và y chiếc bàn.

Diện tích của x chiếc ghế là $0,5x\left( {{m^2}} \right)$ $0,5x\left( {{m^2}} \right)$và y chiếc bàn là $1,2y\left( {{m^2}} \right)$ $1,2y\left( {{m^2}} \right)$

Bước 2: Biểu diễn diện tích lưu thông và cho lớn hơn hoặc bằng $12 {m^2}.$ $12 {m^2}.$

Tổng diện tích x chiếc ghế và y chiếc bàn là $0,5x + 1,2y\left( {{m^2}} \right)$ $0,5x + 1,2y\left( {{m^2}} \right)$

Diện tích lưu thông là $60 - 0,5x - 1,2y\left( {{m^2}} \right)$ $60 - 0,5x - 1,2y\left( {{m^2}} \right)$

Bất phương trình cần tìm là

$\begin{array}{l}60 - 0,5x - 1,2y \ge 12\\ \Leftrightarrow 0,5x + 1,2y \le 48\end{array}$ $\begin{array}{l}60 - 0,5x - 1,2y \ge 12\\ \Leftrightarrow 0,5x + 1,2y \le 48\end{array}$

+) Thay x=10, y=10 ta được

$0,5.10 + 1,2.10 = 17 \le 48$ $0,5.10 + 1,2.10 = 17 \le 48$

=> (10;10) là nghiệm của bất phương trình

+) Thay x=10, y=20 ta được

$0,5.10 + 1,2.20 = 29 \le 48$ $0,5.10 + 1,2.20 = 29 \le 48$

=> (10;20) là nghiệm của bất phương trình

+) Thay x=20, y=10 ta được

$0,5.20 + 1,2.10 = 22 \le 48$ $0,5.20 + 1,2.10 = 22 \le 48$

=> (20;10) là nghiệm của bất phương trình

Bài 5 trang 24 SGK Toán 10

Trong 1 lạng (100 g thịt bò chứa khoảng 26 g protein, 1 lạng cá rô phi chứa khoảng 20 g protein. Trung bình trong một ngày, một người phụ nữ cần tối thiểu 46 g protein. Gọi x, y lần lượt là số lạng thịt bò và số lạng cá rô phi mà một người phụ nữ nên ăn trong một ngày. Viết bất phương trình bậc nhất hai ẩn x, y để biểu diễn lượng protein cần thiết cho một người phụ nữ trong một ngày và chỉ ra ba nghiệm của bất phương trình đó.

Gợi ý đáp án

Bước 1: Biểu diễn lượng protein có trong x lạng thịt bò và y lạng cá rô phi.

Lượng protein trong x lạng thịt bò là 26x (g)

Lượng protein trong y lạng cá rô phi là 20y (g)

Lượng protein trong x lạng thịt bò và y lạng cá rô phi là 26x+20y (g).

Bước 2: Biểu diễn bất phương trình.

Vì lượng protein tối thiểu là 46g nên ta có bất phương trình:

$26x + 20y \ge 46$ $26x + 20y \ge 46$

Bước 3: Tìm nghiệm của bất phương trình

Thay x=1, y=1 vào bất phương trình ta được

Thay x=2, y=1 vào bất phương trình ta được

Thay x=1, y=2 vào bất phương trình ta được